ESSAY

Christian Eurich

neuronale Netzwerke

Neuronale Netzwerke oder neuronale Netze sind mathematische Strukturen, die biologischen Nervenverbänden (Nervensystem) nachempfunden sind. Sie bestehen aus vergleichsweise einfach aufgebauten Einheiten, den Modellneuronen, die über Verbindungsstrecken und Kopplungsstellen (Synapsen) miteinander wechselwirken. Zur Unterscheidung von natürlichen neuronalen Netzen spricht man mitunter auch von künstlichen neuronalen Netzen, engl. Artificial Neural Networks (Nervennetzhypothese).
Seit dem Erscheinen des durch neurobiologische Überlegungen motivierten Artikels "A logical calculus of the ideas immanent in nervous activity" von Warren McCulloch und Walter Pitts im Jahr 1943 hat sich das Gebiet der neuronalen Netze in verschiedene Richtungen entwickelt, die zum Teil gänzlich außerhalb der ursprünglich intendierten neurobiologischen Anwendungsfelder liegen ( vgl. Abb. 1 ). Ein wichtiger Zweig, der in diesem Artikel behandelt werden soll, verwendet neuronale Netze zur Modellierung neurobiologischer, psychophysischer, psychologischer und linguistischer Phänomene. Als Beispiele seien Eigenschaften sensorischer und motorischer Verarbeitung (visuelles Auflösungsvermögen, Koordination von Bewegungen [Motorik, Muskelkoordination] usw.), aber auch kognitive Leistungen wie Aufmerksamkeit (Bewußtsein, visuelle Aufmerksamkeit) und Gedächtnis genannt.
Ein weiterer Zweig der Theorie neuronaler Netze beschäftigt sich mit deren mathematischen und computationalen Eigenschaften. Beispiele dafür sind die Approximation von Funktionen und die automatische Klassifikation von Daten (Datum). Mathematische Eigenschaften neuronaler Netze werden zum Teil auch im Hinblick auf das obengenannte Gebiet der Modellierung biologischer Nervennetze untersucht.
Die Flexibilität neuronaler Netzwerke durch die Anpassung der Synapsenstärken hat außerdem zu Anwendungen in Technik (Bionik) und Wirtschaft geführt; z.B. bei der Wiedererkennung verrauschter Muster (Rauschen, Mustererkennung) in der Bildverarbeitung, der Vorhersage von Zeitreihen und der Steuerung autonomer Roboter. Hier dienen neuronale Netze nicht als Modell für biologische Nervennetze, sondern haben den Status flexibler mathematischer Werkzeuge. Obwohl neuronale Netze zumeist auf herkömmlichen Computern implementiert werden, ist in den letzten Jahren spezielle, auf Parallelverarbeitung basierende Hardware entwickelt worden, die eine schnelle Simulation auch großer Netze ermöglicht (Computersimulation).
Diejenigen Teilbereiche der Theorie neuronaler Netze, die sich mit biologischer Modellierung befassen, sind ihrerseits ein Teil der Theoretischen Neurowissenschaften. Letztere umfassen auch Gebiete, die sich nicht unmittelbar mit der Funktionsweise von Neuronen (Nervenzellen) oder Neuronenverbänden beschäftigen, z.B. phänomenologische Modellbildung im Bereich der Psychophysik und Psychologie sowie Datenauswertung in der Elektrophysiologie oder bei bildgebenden Verfahren.
Im nächsten Abschnitt wird ein kurzer Überblick über die Neurobiologie (Neurobiologie, Geschichte der) der Nervenzelle gegeben. Im Anschluß daran werden einige Standardmodelle für Neurone vorgestellt, die in der Theorie neuronaler Netze verwendet werden. Im weiteren Verlauf des Essays werden exemplarisch Themen erläutert, die in der Modellierung neuronaler Systeme eine wichtige Rolle spielen: Hopfield-Netze als Modelle für die Speicherung von Gedächtnisinhalten, neuronale Synchronisation und selbstorganisiertes (Hebbsches) Lernen.

Neurobiologie der Nervenzelle

Biologische Neurone dienen der Aufnahme, Verarbeitung und Weiterleitung von Signalen ( vgl. Abb. 2 ). Diese Signale haben die Form raumzeitlicher Spannungsänderungen (Potentialänderungen; Potential) über der Zell-Membran. Im Ruhezustand ist das Zellinnere gegenüber dem Außenraum negativ geladen, und die Spannung beträgt ca. (–)70 mV (Membranpotential, Ruhepotential).
Die Dendriten stellen die Eingangsfasern des Neurons dar. Sie sind mit bis zu 10.000 Kontaktstellen, den Synapsen, besetzt, über die das Neuron Signale von anderen Nervenzellen empfängt. Die Signale breiten sich im Dendritenbaum bis zum Zellkörper (Soma, Perikaryon) aus. Überschreitet durch Depolarisation die Spannung an der Soma-Membran einen Schwellenwert von ca. –40 mV, so wird am Ansatzpunkt der Nervenfaser (Axon) eine pulsförmige elektrische Welle (Aktionspotential, Spike) ausgelöst, die ungedämpft entlang der Nervenfaser zu den axonalen Endigungen läuft: das Neuron feuert. Zur Erhöhung der Signalgeschwindigkeit sind manche Axone von einer isolierenden Proteinschicht, der Myelinscheide (Markscheide), umgeben. An den axonalen Endigungen schließlich wird das elektrische Signal über Synapsen an nachgeschaltete Neurone oder Muskelzellen (Muskeln, Muskulatur) übertragen.
Die synaptische Signalübertragung erfolgt entweder durch direkte elektrische Kopplung oder auf chemischem Wege. Bei der chemischen Synapse bewirkt ein ankommendes Aktionspotential in der vorgeschalteten Zelle die Ausschüttung von Transmitterstoffen (Neurotransmitter), die zur nachgeschalteten Zelle diffundieren (Diffusion) und dort aufgenommen werden. Als Folge davon kommt es in der nachgeschalteten Zelle ebenfalls zu einer Änderung der Membranspannung, zu einem postsynaptischen Potential. Chemische Synapsen können erregend (excitatorisch; erregendes postsynaptisches Potential) oder hemmend (inhibitorisch; hemmendes postsynaptisches Potential, hemmende Synapse) wirken – je nach Vorzeichen des postsynaptischen Potentials.
Wird eine Nervenzelle erregt (Erregung), so antwortet sie im allgemeinen mit einer Serie von Aktionspotentialen, einem Spiketrain ( vgl. Abb. 3 ). Der zeitliche Abstand zweier Spikes kann dabei nicht beliebig klein sein, da die Zelle nach der Erzeugung eines Spikes eine kurze Zeit von wenigen Millisekunden, die Refraktärzeit, zur Regeneration benötigt.

Neuronenmodelle

Die Neurone künstlicher neuronaler Netze besitzen wesentliche Eigenschaften biologischer Nervenzellen, und ihre Wechselwirkung orientiert sich an der elektrischen und chemischen Signalübertragung im Gehirn. Für die Modellierung neurobiologischer Systeme wird unterschiedlich stark von den komplexen Eigenschaften realer Neurone abstrahiert. Dementsprechend existiert eine Reihe von Neuronenmodellen, die sich hinsichtlich ihrer biologischen Detailtreue unterscheiden. Grundsätzlich ist das einfachste Modell zu bevorzugen, das in der Lage ist, betrachtete Phänomene zu erklären. Auf diese Weise reduzieren sich Wahlfreiheiten innerhalb des Modells, und es ist möglich, Mechanismen für das beobachtete Systemverhalten zu extrahieren (System, Systemanalyse).
Abb. 4 zeigt sehr einfache Neuronenmodelle, die in Netzwerken benutzt werden, die keine kontinuierliche Zeitstruktur besitzen, sondern in diskreten Zeitschritten aktualisiert werden. Das bedeutet, daß ein Neuron in jedem Zeitschritt Eingaben bekommt, die zu einer Reaktion (Ausgabe) dieses Neurons führen. Die Ausgabe kann im darauffolgenden Zeitschritt wiederum als Eingabe für andere Neurone des Netzwerks dienen. Bei dem in Abb. 4a dargestellten Neuron sind die Eingaben mit y₁, ..., y_n bezeichnet; sie stammen entweder von anderen Neuronen oder stellen äußere Eingaben in das Netzwerk dar. Die Eingaben werden mit Synapsenstärken w₁, ..., w_n gewichtet. Die biologische Wirkung einer Synapse wird hier also durch eine einfache Multiplikation mit einer reellen Zahl modelliert. Ist eine Synapsenstärke w_i (i = 1, ..., n) positiv, so wirkt die zugehörige Eingabe y_i excitatorisch, für negative Synapsenstärke dagegen inhibitorisch. Die gesamte Aktivierung h des Neurons – interpretierbar z.B. als Depolarisation der Zellmembran am Soma – erhält man durch Summation aller gewichteten Eingaben: h = w₁ y₁ + ... + w_ny_n. Die Ausgabe y des Neurons wird dadurch ermittelt, daß eine Funktion f, die sog. Ausgabefunktion, auf die Aktivierung h angewendet wird: y = f(h). Verschiedene Neuronenmodelle ergeben sich nun durch unterschiedliche Wahl möglicher Ein- und Ausgabewerte und Ausgabefunktionen.
Beim McCulloch-Pitts-Neuron sind die möglichen Eingaben und die Ausgabe binär (y₁, ..., y_n, y = 0 oder 1) und werden als "Feuern" bzw. "Nicht-Feuern" des Neurons interpretiert. Als Ausgabefunktion wird eine Stufenfunktion gewählt, die den Ausgabewert y = 0 liefert, falls die Aktivierung h des Neurons unterhalb eines Schwellenwerts (der sog. Feuerschwelle) liegt, und ansonsten den Ausgabewert y = 1 ( vgl. Abb. 4b ). Aus rechnerischen Gründen werden anstatt der Ausgabewerte 0 und 1 des Neurons mitunter die Werte –1 und 1 gewählt, was aber nichts an der Interpretation des Modells ändert.
Nehmen die Eingaben y₁, ..., y_n und die Ausgabe y kontinuierliche (reelle) Werte an, spricht man von einem Analogneuron, und die Ausgabe y wird als mittlere Anzahl von Spikes interpretiert, die das Neuron pro Zeiteinheit erzeugt (Feuerrate). Für Analogneurone verwendet man typischerweise eine sigmoide Ausgabefunktion, d.h. eine stetige und monoton steigende Funktion, die von null auf einen Maximalwert y_max, der maximal möglichen Feuerrate, ansteigt ( vgl. Abb. 4c ).
In vielen Fällen ist eine Modellierung in diskreten Zeitschritten nicht ausreichend, z.B. bei der Analyse neuronaler Synchronisation. In solchen Fällen greift man auf Neuronenmodelle zurück, die eine reelle Zeitvariable aufweisen. Damit wird es z.B. möglich, nicht nur die räumliche Summation an einem Neuron, also die kombinierte Wirkung verschiedener Eingaben, zu betrachten, sondern auch die zeitliche Summation, also die Wirkung zeitlich aufeinanderfolgender Eingaben. Neuronenmodelle, bei denen Aktionspotentiale berücksichtigt werden, werden in der Theorie als spikende Neurone bezeichnet. Das gebräuchlichste Neuronenmodell dieser Art ist das Integrate-and-Fire-Neuron, das die zeitliche Dynamik des neuronalen Membranpotentials beschreibt. Das Modell ist insofern einfach, als das Neuron keine räumliche Struktur aufweist, sondern lediglich durch ein einziges Membranpotential V charakterisiert ist, das sich in der Zeit t ändert: V = V(t). Das Ruhepotential des Neurons wird zumeist auf Null gesetzt; damit bekommt V die Interpretation der Abweichung vom Ruhepotential.
Das Zeitverhalten von V ergibt sich aus zwei elementaren Eigenschaften der Zellmembran. Zum einen sind die Konzentrationen verschiedener Ionensorten (Anion, Kation) im Innen- und Außenraum der Zelle unterschiedlich, was mit einer Ladungstrennung (elektrische Ladung) einhergeht. Entlang der Membran lagern sich deshalb Ionen an: die Membran weist eine elektrische Kapazität C auf, ähnlich einem Plattenkondensator. Zum anderen existieren unterschiedliche Ionenströme durch die Membran, z.B. Pumpströme und geschaltete Ströme durch Ionenkanäle. Im Modell werden lediglich diejenigen Ströme berücksichtigt, die nach einer Depolarisation oder Hyperpolarisation die Rückkehr zum Ruhepotential bewirken; diese sind durch einen Ohmschen Widerstand R charakterisiert. Die komplexen Membranströme, die während eines Aktionspotentials auftreten, bleiben dagegen unberücksichtigt. Eingaben in das Neuron, z.B. aufgrund von Spike-Aktivitäten anderer Neurone im Netzwerk, werden durch explizite Angabe eines Stroms I(t) modelliert.
Unterhalb der neuronalen Feuerschwelle läßt sich das Zeitverhalten des Membranpotentials V quantitativ durch eine Differentialgleichung beschreiben, die sich nach J.C. Eccles aus dem in Abb. 5 gezeigten Stromkreis, dem sog. Ersatzschaltbild des Neurons, ergibt. Um die Erzeugung von Aktionspotentialen zu berücksichtigen, wird zusätzlich eine Feuerschwelle angenommen. Überschreitet das Membranpotential zu einer bestimmten Zeit diese Schwelle, so gibt das Neuron einen Spike ab, und das Membranpotential wird anschließend auf Null gesetzt. Für die bei einem Neuron ankommenden Spikes wählt man z.B. einen kurzen, pulsartigen Strom I(t); dieser führt zu einer sprunghaften Änderung des Membranpotentials mit anschließender exponentieller Rückkehr zum Ruhepotential V = 0. Alternativ läßt sich die Form postsynaptischer Potentiale detaillierter durch Verwendung einer anderen Stromfunktion modellieren; hier wird meist die sog. Alpha-Funktion verwendet ( vgl. Abb. 5b ). Refraktärzeiten können zusätzlich durch eine zeitabhängige Feuerschwelle berücksichtigt werden.
Neben den beschriebenen gibt es weitere, insbesondere komplexere Neuronenmodelle. Zur Berücksichtigung der räumlichen Struktur eines Neurons verwendet man häufig sog. Kompartimentmodelle, bei denen das Neuron in miteinander verbundene Abschnitte unterteilt wird, die ähnlich wie das Integrate-and-Fire-Neuron durch Kapazitäten und Widerstände charakterisiert sind. Zur genaueren Modellierung von Aktionspotentialen werden in vielen Fällen die Hodgkin-Huxley-Gleichungen herangezogen, die z.B. ein "spikendes" Kompartiment in einem Kompartimentmodell bilden können. Zur Simulation größerer Netzwerke verwendet man wegen des geringeren Rechenaufwandes jedoch meist einfache Neuronenmodelle.

Das Hopfield-Modell

John Hopfield schlug 1982 ein neuronales Netz vor, dem durch bestimmte Wahl der Synapsenstärken räumliche Muster aufgeprägt werden können, und das bei späterer Präsentation eines verrauschten oder unvollständigen Musters in der Lage ist, diese Muster zu reproduzieren. Ein solches System wird als Assoziativspeicher bezeichnet. Die Reproduktion der gespeicherten Muster weist z.B. Analogien zur Fähigkeit von Menschen auf, den vollständigen Namen einer Person zu erinnern, wenn der Vorname vorgegeben wird.
Ein Hopfield-Netz besteht aus N McCulloch-Pitts-Neuronen, wobei als mögliche Ausgabewerte –1 (nicht aktiv) und 1 (aktiv) gewählt werden. Alle Neurone sind miteinander verbunden. Bekommt ein beliebiges Neuron i (i = 1, ..., N) im Zeitschritt t die Eingaben y₁(t), ..., y_N(t), so berechnet sich seine Ausgabe im nächsten Zeitschritt t +1 gemäß y_i(t +1) = f(w_i1y₁ (t) + ... + w_iNy_N(t)); dabei ist f die im vorigen Abschnitt beschriebene Stufenfunktion, und w_i1, ..., w_iN stellen die Synapsenstärken dar, mit denen die Neurone des Netzes auf Neuron i projizieren.
Durch geeignete Wahl dieser Synapsenstärken w_ij (i, j = 1, ..., N) ist es möglich, vom Benutzer gewünschte Aktivitätsmuster im Netzwerk zu speichern. Sei das m-te Muster (m = 1, ..., M) gegeben durch die N Neuronenaktivitäten

, dann sind die Synapsenstärken w_ij (i, j = 1, ..., N) gemäß der Vorschrift

zu wählen.
Abb. 6 zeigt oben ein einzelnes Muster, das einem Netzwerk aus 4096 Neuronen aufgeprägt wurde ( vgl. Abb. 6 ). Die Neurone sind im Quadrat angeordnet, und die beiden möglichen Aktivitätswerte –1 und 1 sind weiß bzw. schwarz codiert. Anschließend kann man das Netz mit einem unvollständigen (links) oder verrauschten (rechts) Muster starten. In jedem Zeitschritt wird zufällig ein Neuron ausgewählt, dessen Aktivität nach der oben beschriebenen Vorschrift berechnet wird. Nach mehreren Schritten stellt das Netz das eingespeicherte Muster wieder her. Sind mehrere Muster gespeichert, so wird vom Netz dasjenige ausgewählt, das die größte Ähnlichkeit mit dem Startmuster aufweist.
In einem Hopfield-Netz lassen sich nicht beliebig viele Muster speichern. Rechnungen zeigen, daß die Speicherkapazität M ˜ 0,138 N Muster beträgt; darüber hinaus kann keine Stabilität der Muster mehr erwartet werden. Die besten Speichereigenschaften hat das Hopfield-Netz für voneinander unabhängige Zufallsmuster, was bei realen Bildern im allgemeinen nicht der Fall ist.

Synchronisation in Netzen aus spikenden Neuronen

Seit dem Ende der 1980er Jahre erfährt das Thema der Aktivität in Netzen aus spikenden Neuronen starkes Interesse. Eine Motivation für die theoretischen Arbeiten war unter anderem die Vermutung, daß die Zeitstruktur der Spike-Aktivität in neuronalen Populationen – im Gegensatz z.B. zur Feuerrate, also zur bloßen Anzahl von Aktionspotentialen pro Zeitintervall – funktionale Bedeutung hat. Insbesondere wurde dem synchronen Feuern (d.h. dem Feuern in konstanten Zeitabständen, zumeist dem gleichzeitigen Feuern) eine Rolle bei der Gestaltwahrnehmung und der verhaltensrelevanten Objektwahrnehmung zugeschrieben. Theoretische Untersuchungen zur Synchronisation werden zumeist anhand eines einfachen Neuronenmodells wie dem Integrate-and-Fire-Neuron durchgeführt, da entsprechende Netzwerke teilweise einen analytischen Zugang erlauben und zudem vergleichsweise einfach zu simulieren sind. In den meisten Modellen bekommen die Modellneurone einen konstanten Eingabestrom. Unter diesen Bedingungen produziert ein Einzelneuron in periodischen Abständen Aktionspotentiale: es wird zum Oszillator.
Renato E. Mirollo und Steven H. Strogatz studierten 1991 die Dynamik von Netzwerken identischer, vollständig excitatorisch miteinander gekoppelter spikender Modellneurone. Sie zeigten, daß solche Netzwerke für fast alle Anfangsbedingungen in einen Zustand evolvieren, in dem die Neurone synchron mit der Phasenlage Null (also gleichzeitig) feuern. Diese Untersuchung ist hinsichtlich mehrerer Aspekte erweitert worden. Sind die Neurone inhibitorisch gekoppelt, so stellt sich ein Netzwerkzustand ein, in dem die Neurone möglichst zu unterschiedlichen Zeitpunkten feuern: die Oszillatoren nehmen unterschiedliche Phasenlagen ein. Werden zusätzlich Signallaufzeiten zwischen den Neuronen, die in realen Systemen stets auftreten, berücksichtigt, so ergibt sich ein anderes Bild: inhibitorische Kopplungen führen zur Bildung stabiler Teilpopulationen (Clustern) von Neuronen, die jeweils synchron feuern. Bei excitatorischer Kopplung dagegen sind die sich ausbildenden Cluster nicht stabil, sondern zerfallen nach einigen Feuerperioden wieder und bilden sich spontan neu mit wechselnder neuronaler Zusammensetzung. Schließlich kann man Netzwerke aus Neuronen studieren, die sich hinsichtlich ihrer Membraneigenschaften, der Stärke ihres Eingabestroms usw. unterscheiden. Hier ergibt sich eine reiche Phänomenologie. Beispielsweise treten bereits bei Netzwerken aus nur zwei Neuronen verschiedene Aktivitätsrhythmen mit gleichzeitigem oder nicht-gleichzeitigem Feuern und Bistabilitäten auf.

Lernen in neuronalen Netzen

Eine wesentliche Eigenschaft von Menschen und Tieren ist ihre Fähigkeit, aufgrund von Erfahrungen die Wahrnehmung und das Verhalten zu ändern. Die Ursache dafür ist eine Adaptationsfähigkeit (Adaptation) des Nervensystems auf zellulärer und subzellulärer Ebene.
Die Verhaltensweisen künstlicher neuronaler Netze hängen wesentlich von den Synapsenstärken ab, mit denen die Neurone untereinander verknüpft sind. Eine Änderung dieser Synapsenstärken kann deshalb dazu benutzt werden, die Eigenschaften eines Netzes an gewünschte Aufgaben anzupassen. Damit bekommen künstliche neuronale Netze neben der Aktivität der Neurone (neuronale Dynamik) eine zeitliche Entwicklung der Synapsenstärken (Lerndynamik). Lernverfahren (Lernen) in neuronalen Netzen lassen sich grob in 3 Kategorien einteilen: beim überwachten Lernen wird nach einer Eingabe in das Netz ein Fehler, also eine Diskrepanz zwischen der tatsächlichen und der erwarteten Ausgabe des Netzes, ausgewertet; dieser Fehler wird verwendet, um die Synapsenstärken zu ändern. Beim unüberwachten Lernen wird eine solche Information über fehlerhaftes Verhalten nicht zur Verfügung gestellt, sondern die Veränderungen im Netz sind selbstorganisiert. Zwischen diesen Extremen liegt das Reinforcement-Lernen, bei dem das Netzwerk nur wenig Information erhält, z.B. die binäre Auskunft "gut" oder "schlecht".
Hinsichtlich der direkten Übertragbarkeit der Lernverfahren in künstlichen neuronalen Netzen auf die Adaptationsfähigkeit im Nervensystem ist Vorsicht geboten. Auf der einen Seite sind nicht alle Lernalgorithmen, die in der Theorie neuronaler Netze entwickelt werden, biologisch plausibel. Von biologischer Relevanz ist insbesondere das selbstorganisierte Lernen, von dem in den nächsten beiden Abschnitten die Rede sein wird. Auf der anderen Seite scheinen Adaptationsvorgänge im Nervensystem weitaus vielschichtiger zu sein, als dies durch gegenwärtige Lernverfahren in künstlichen neuronalen Netzen erfaßbar wäre. Im Nervensystem besteht eine enge Abhängigkeit zwischen der Funktion eines Netzwerks und der zugrundeliegenden neuronalen Struktur (Morphologie der Nervenzellen, Struktureigenschaften der Membran usw.). Derartige Wechselbeziehungen sind bislang kaum theoretisch erarbeitet.

Hebbsches Lernen

Der kanadische Psychologe D.O. Hebb stellte 1949 die Hypothese auf, daß Lernvorgänge im Nervensystem anatomischen oder physiologischen Veränderungen auf zellulärer oder subzellulärer Ebene entsprechen, die von einer zeitlich korrelierten Aktivität der entsprechenden Nervenzellen abhängen (Hebbsches Postulat; Hebbsche Regel). Der vorgeschlagene Mechanismus ist lokaler Natur: die Plastizität, die durch die Aktivität zweier miteinander verschalteter Neurone ausgelöst wird, betrifft lediglich eben diese Neurone. Das Hebbsche Postulat hat zu einem bis heute andauernden intensiven Forschungsprogramm geführt, das zum Ziel hat, Erscheinungsformen, Bedingungen und Mechanismen neuronaler Plastizität aufzuklären. Ein wesentlicher Fortschritt auf diesem Gebiet war die Entdeckung der Langzeitpotenzierung (LTP) und der Langzeitdepression (LTD) in den 1980er Jahren.
Auf theoretischer Seite entspricht der lokale Charakter des von Hebb postulierten Mechanismus einem unüberwachten Lernen. Es wurden einfache, auf wechselseitiger Aktivität von Neuronen beruhende Lernregeln für neuronale Netze mit diskreter Zeitstruktur entwickelt (vgl. in Lit.: Brown et al., 1990). Die einfachste Variante einer sog. Hebbschen Regel lautet
w_ij(t +1) = w_ij(t) + εy_i(t)y_j(t). Die neue Synapsenstärke w_ij zur Zeit t +1, mit der Neuron j auf Neuron i einwirkt, ist gleich der alten Synapsenstärke zur Zeit t plus einem Lernfaktor ε (einer kleinen Zahl zwischen Null und Eins), multipliziert mit dem Produkt der Ausgaben y_i und y_j der beteiligten Neurone zur Zeit t. Das Hebbsche Postulat kommt in dieser Lernregel insofern zum Tragen, als die Ausgaben beider Neurone notwendig sind, um eine Änderung der Synapsenstärke zu bewirken. Zuweilen wird in der Lernregel nicht die Ausgabe y_i, sondern die Aktivierung h_i(t) des nachgeschalteten Neurons verwendet,
w_ij(t +1) = w_ij(t) + εh_i(t)y_j(t). Mit der Hebbschen Regel ist es z.B. möglich, nacheinander verschiedene Muster in einem Netzwerk zu speichern und dieses als Assoziativspeicher zu verwenden. Tatsächlich hat die oben beschriebene Wahl der Gewichte beim Hopfield-Netz die Form einer Hebbschen Lernregel.
Ein Problem der Hebbschen Lernregel besteht darin, daß sie zu Instabilitäten in Netzwerken führt: eine bereits große Synapsenstärke bewirkt eine starke Aktivierung des nachgeschalteten Neurons und damit eine weitere Erhöhung der Synapsenstärke. Abhilfe schafft hier z.B. eine globale Skalierung aller Synapsenstärken eines postsynaptischen Neurons; dies entspricht mathematisch einem Wettbewerb zwischen den Synapsen. Eine derartige synaptische Skalierung ist experimentell nachgewiesen worden (vgl. in Lit.: Abbott und Nelson, 2000).
Auf experimenteller Seite wurden in den vergangenen Jahren die exakten zeitlichen Bedingungen für das Auftreten von LTP und LTD aufgeklärt (vgl. in Lit.: Abbott und Nelson, 2000). Es konnte nachgewiesen werden, daß eine Verstärkung der Synapse durch LTP stattfindet, wenn die vorgeschaltete Zelle wenige Millisekunden vor der nachgeschalteten Zelle ein Aktionspotential produziert, wenn es also eine kausale Einwirkung der vor- auf die nachgeschaltete Zelle gibt. Ist hingegen das Signal der vorgeschalteten Zelle verspätet, so findet LTD statt: die zeitliche Korrelation der Signale kann in diesem Fall nur zufällig sein. Trägt man die Stärke von LTP bzw. LTD als Funktion des zeitlichen Abstandes zwischen der Aktivität der vor- und der nachgeschalteten Zelle auf, erhält man ein sog. Lernfenster ( vgl. Abb. 7 ). Die Existenz eines solchen Lernfensters legt nahe, daß die zeitliche Abfolge der Aktionspotentiale im Nervensystem eine große Rolle für plastische Veränderungen spielt.
Zeitabhängiges Hebbsches Lernen läßt sich in Netzwerken aus spikenden Neuronen untersuchen. Betrachtet man eine Synapse, mit der Neuron j auf Neuron i einwirkt, dann wird aufgrund eines Spikes zur Zeit t_j im vorgeschalteten Neuron und eines Spikes zur Zeit t_i im nachgeschalteten Neuron die Synapse gemäß der folgenden Lernregel verändert:

, wobei die Funktion W das in Abb. 7 dargestellte Lernfenster ist. Lernen erfolgt dann zwischen allen Spike-Paaren von miteinander verschalteten Neuronen. Es wurde gezeigt, daß zeitsensitives Hebbsches Lernen automatisch zu einem Wettbewerb zwischen Synapsen führt, was ein ständiges Anwachsen der Netzwerkaktivität verhindert. Anwendungen der zeitsensitiven Hebbschen Lernregel existieren mittlerweile auf den Gebieten der Koinzidenzdetektion (z.B. im auditorischen System der Schleiereule; Koinzidenz, Koinzidenzelement), der Adaptivität der Richtungsselektivität neuronaler Antworten im visuellen System und dem Erlernen räumlicher Navigation.

Ausblick

Das Gebiet der neuronalen Netze mit seiner etwas über 50jährigen Geschichte zeigt sich nach wie vor unvollendet. Dies betrifft sowohl die Erforschung der mathematischen Eigenschaften von Netzwerken als auch ihre Anwendung auf neurobiologische Systeme. Kennzeichnend für das Gebiet ist eine wechselseitige Befruchtung von Experiment und Theorie, was sich z.B. stark in der Entwicklung der Netzwerke aus spikenden Neuronen niedergeschlagen hat. Weitere biologisch relevante Themen, die in diesem Artikel nicht behandelt werden konnten, sind die Theorie selbstorganisierender Merkmalskarten, die im Gehirn bezüglich verschiedener Sinnesmodalitäten (Modalität) zu finden sind, und die neuronale Codierung. Bei letzterem wird die Frage gestellt, welche Eigenschaften einer neuronalen Population (Art des verwendeten neuronalen Codes, Tuning-Eigenschaften, Korrelationen in der neuronalen Antwort usw.) die genaue Repräsentation sensorischer Reize oder motorischer Handlungen erlauben, die man in psychophysischen Experimenten oder im Verhalten beobachtet. In diesem Zusammenhang lassen sich möglicherweise auch mentale Zustände (z.B. die Steuerung von Aufmerksamkeit) untersuchen und quantitativ erfassen. Neuronale Netze werden auch in Zukunft eine wichtige Klasse von Modellen darstellen, die zu einem Verständnis der Vorgänge im Nervensystem beitragen. Biokybernetik, Biophysik, Biotechnik, Denken, Feedback, Funktionsschaltbild, Fuzzy-Logik, Gesichtererkennung, Information, Kontrollsystemtheorie, künstliche Intelligenz, künstliches Leben, Synergetik, Systemtheorie.

Lit.: Abbott, L.F., Nelson, S.B.: Synaptic plasticity: taming the beast. In: Nature Neuroscience Suppl. 3 (2000), 1178–1183. Arbib, M.A. (Ed.): The Handbook of Brain Theory and Neural Networks. Cambridge 1995. Braun, H.: Neuronale Netze. Optimierung durch Lernen und Evolution. Berlin – Heidelberg 1997. Brown, T.H., Kairiss, E.W., Keenan, C.L.: Hebbian synapses: Biophysical mechanisms and algorithms. In: Annu. Rev. Neurosci. 13 (1990) 475–511. Dayan, P., Abbott, L.F.: Theoretical Neuroscience. Cambridge 2001. Maass, W., Bishop, C.M. (Ed.): Pulsed Neural Networks. Cambridge 1999. Rieke, F., Warland, D., de Ruyter van Steveninck, R., Bialek, W.: Spikes –Exploring the Neural Code. Cambridge 1997. Ritter, H., Martinetz, T., Schulten, K.: Neuronale Netze. Bonn 1991. Rojas, R.: Theorie der neuronalen Netze. Berlin 1993. Zell, A.: Simulation neuronaler Netze. München 1994. Zhang, L.I., Tao, H.W., Holt, C.E., Harris, W.A., Poo, M.-M.: A critical window for cooperation and competition among developing retinotectal synapses. Nature 395 (1998) 37–44.

Abb. 1: Teildisziplinen des Forschungsgebiets der neuronalen Netze und – zum Teil damit überlappend – einige Forschungsbereiche der Theoretischen Neurowissenschaften. In diesem Artikel werden Aspekte der Modellierung biologischer Nervennetze beschrieben (fett umrandeter Kasten).

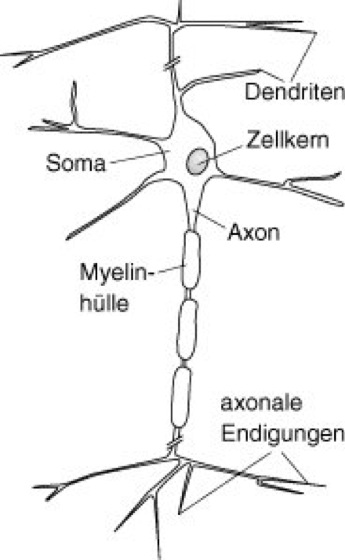
Abb. 2: Schematische Darstellung eines biologischen Neurons

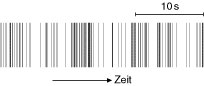
Abb. 3: Beispiel für einen Spiketrain eines Neurons aus dem primären visuellen Cortex einer Ratte; dem anästhesierten Tier wurde ein bewegtes Gittermuster mit bestimmter Orientierung präsentiert. Jedes Aktionspotential ist idealisiert als Strich dargestellt. Skala: 10 s. (nach W. Freiwald und H. Stemmann).

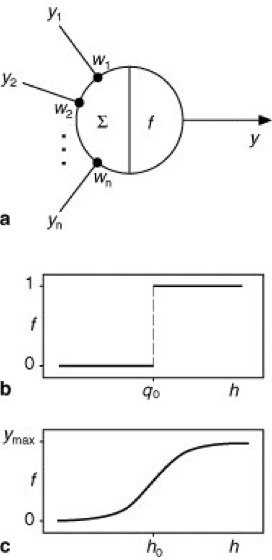
Abb. 4: Neuronenmodelle für Netzwerke mit diskreter Zeitstruktur: a Schematische Darstellung eines Neurons mit Eingaben y₁, ..., y_n, Synapsenstärken w₁, ..., w_n und Ausgabe y. Das Symbol Σ steht für die Berechnung der Aktivierung h des Neurons durch Summenbildung, das Symbol f bezeichnet die Ausgabefunktion zur Ermittlung der Neuronenausgabe y. b Ausgabefunktion f für ein McCulloch-Pitts-Neuron; es existieren nur die möglichen Ausgabewerte y = 0 oder y = 1; q₀ Schwellenwert. c Ausgabefunktion f für ein Analogneuron, bei dem die Ausgabe y beliebige Werte zwischen y = 0 (kein Feuern) und y = y_max (Feuern mit maximaler Feuerrate) annehmen kann; für h = h₀ feuert das Neuron mit der Rate y_max/2.

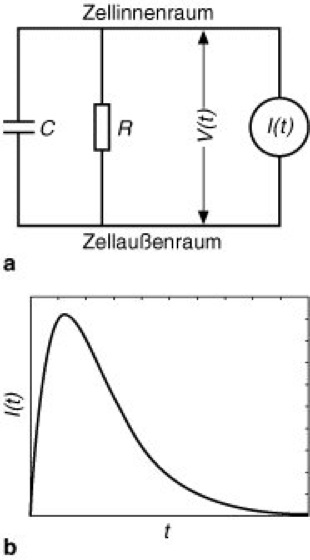
Abb. 5: Das Integrate-and-Fire-Neuron. a Ersatzschaltbild des Neurons unterhalb der Feuerschwelle. Das Membranpotential V(t) ergibt sich als Lösung der Differentialgleichung

.

b Schematischer Verlauf einer Alpha-Funktion zur Modellierung des bei Ankunft eines Aktionspotentials in die Zelle fließenden Stroms. Die Funktion (Exponentialfunktion) ist gegeben durch I(t) = k t e^–αt mit k >0 für Excitation und k <0 für Inhibition; 1/α ist die Zeitkonstante mit der die Funktion I(t) abfällt. Das aus einem solchen Strom resultierende Membranpotential ähnelt einem excitatorischen oder inhibitorischen postsynaptischen Potential (EPSP bzw. IPSP).

Abb. 6: Dynamik eines Hopfield-Netzes: Das Netzwerk besteht aus 4096 Neuronen, die zum Quadrat angeordnet sind; ihre Ausgaben sind schwarz-weiß-codiert. Oben: ein Muster wurde dem Netzwerk aufgeprägt. Linke Spalte: Startet man das Netzwerk mit einem unvollständigen Muster, so erhält man nach mehreren Iterationsschritten das eingespeicherte Bild: das Muster wurde "erkannt". Rechte Spalte: auch ein stark verrauschtes Anfangsmuster führt nach mehreren Iterationsschritten zur richtigen Lösung.

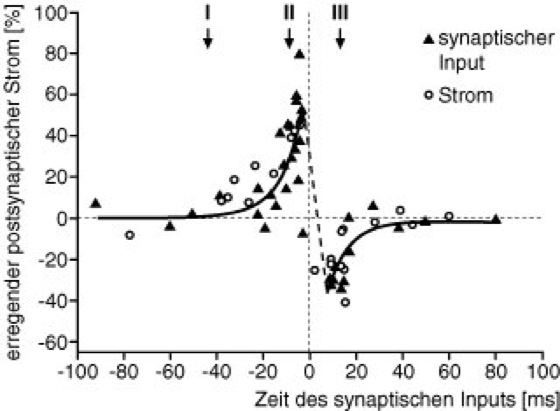
Abb. 7: Hebbsches Lernfenster für Mittelhirnneuronen einer Kaulquappe, die Eingaben von retinalen Ganglienzellen bekommen. Auf der Abszisse ist die Zeitdifferenz zwischen den Aktivitäten der vor- und der nachgeschalteten Zelle aufgetragen, die Ordinate zeigt die Änderung des in die nachgeschaltete Zelle einfließenden Stroms (excitatorischer postsynaptischer Strom, EPSC) aufgrund von 100 elektrischen Stimulationen. In den Gebieten I und II wirkt das vorgeschaltete Neuron kausal auf das nachgeschaltete Neuron ein, und die Synapse wird verstärkt; in Gebiet III ist das korrelierte Auftreten von Aktionspotentialen akausal (zufällig), und die Synapse wird abgeschwächt. (nach Zhang et al., 1998).