Der Mathematische Monatskalender: Zu Chongzhi (429–500): Fasziniert von Kreisen
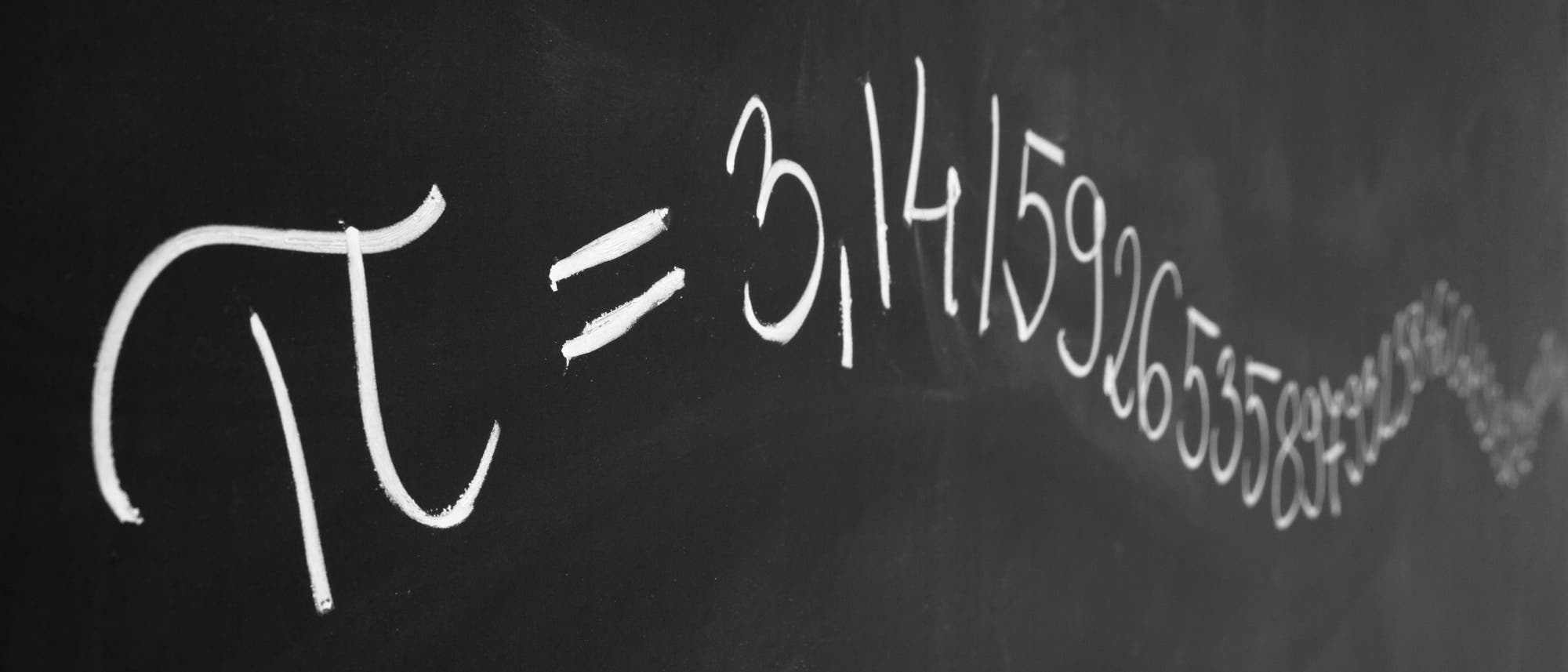
Als besondere Leistung des chinesischen Mathematikers Zu Chongzhi gilt die Bestimmung der Kreiszahl \(\pi\) mit einer Genauigkeit von sieben Dezimalstellen. Diese Genauigkeit wird erst im 15. Jahrhundert, also fast 1000 Jahre später, durch den letzten großen Mathematiker des islamischen Mittelalters, al Kashi, übertroffen und Ende des 16. Jahrhunderts in Europa durch Ludolph van Ceulen. Ab 1670 dann stehen mit der Entwicklung der Differentialrechnung durch Newton und Leibniz völlig andere Berechnungsmethoden zur Verfügung.
Zu Chongzhi ist als Beamter am chinesischen Hof tätig - wie sein Großvater und sein Vater, die ihr astronomisches Wissen und ihre mathematischen Kenntnisse und Fertigkeiten an ihn weitergeben. Im alten China ist man der Ansicht, dass das Recht des Kaisers zu herrschen diesem vom Himmel gegeben werden muss – als Beweis für die himmlische Beauftragung gilt es, wenn ein Herrscher einen neuen Kalender einführt.
In seiner Funktion als hoher Regierungsbeamter bemüht sich Zu Chongzhi in diesem Sinne darum, einen Kalender zu entwickeln, der besser als der bisher verwendete dem Sonnen- und Mondzyklus entspricht. Der zu dieser Zeit gültige Kalender hat einen 19-Jahres-Zyklus mit 235 Monaten (die Monate haben 29 oder 30 Tage; ein chinesischer Monat umfasst die Zeit von Neumond zu Neumond) - 12 Jahre mit zwölf Monaten und 7 Jahre mit einem dreizehnten Monat. Aufgrund seiner präzisen astronomischen Beobachtungen kommt er zum Ergebnis, dass ein Kalender mit einem Zyklus von 391 Jahren mit insgesamt 4836 Monaten, davon 144 Jahre mit 13 Monaten, besser den »himmlischen« Gegebenheiten entspricht - die durchschnittliche Jahreslänge wäre bei dem von ihm vorgeschlagenen Zyklus nur mit einem Fehler von 50 Sekunden gegenüber der wahren Länge eines tropischen Jahres behaftet gewesen.
Es wird vermutet, dass Zu Chongzhi durch Messungen für die Länge eines Jahres den Wert \(365\frac{9589}{39491}\) Tage findet und für den Mond-Monat \(\frac{116321}{3939}\) Tage. Ein Jahr besteht demnach aus \(12\frac{1691772624}{4593632611}\) Monaten; der Bruch lässt sich kürzen und man erhält \(12\frac{ 144}{391}\) , das heißt, in 144 von 391 Jahren ist ein zusätzlicher Mond-Monat erforderlich.
Trotz aller Widerstände und Intrigen am Hof gelingt es Zu Chongzhi, seinen Herrscher davon zu überzeugen, dass dieser kompliziert erscheinende Kalenderzyklus eingeführt werden soll. Da der Kaiser jedoch im Jahre 464 stirbt, bevor die Änderung umgesetzt werden kann, und der nachfolgende Herrscher sich nicht der Meinung seines Vorgängers anschließt, wird die neue Zeitrechnung nicht eingeführt.
Zu Chongzhi zieht sich vom kaiserlichen Hofe zurück und widmet sich nur noch der Mathematik und der Astronomie. Zusammen mit seinem Sohn Zu Geng verfasst er ein Mathematikbuch mit dem Titel »Zhui shu« (Methode der Interpolation), das große Anerkennung findet und zu den berühmten Zehn Klassikern der chinesischen Mathematik gezählt wird. Wegen seines hohen Anspruchs wird es jedoch bald aus dem Pflichtkanon der kaiserlichen Akademie gestrichen (jeder, der Beamter am kaiserlichen Hof werden möchte, muss auch eine anspruchsvolle Prüfung in Mathematik ablegen). Im Jahr 1084 noch einmal nachgedruckt, verliert sich im 12. Jahrhundert jede Spur von diesem Buch.
Zu Chongzhi gibt in seinem Buch für die Kreiszahl \(\pi\) den Näherungsbruch \(\frac{355}{113}\) an. Schreibt man diese Zahl als Kettenbruch, so erhält man: \(\frac{355}{113}=3+\frac{16}{113}=3+\frac{1}{7+\frac{1}{16}}\).
Lässt man bei diesem Kettenbruch den letzten Summanden weg, ergibt sich für \(\pi\) der Näherungsbruch \(3\frac{1}{7} = \frac{22}{7}\), ein Wert, der bereits von Archimedes angegeben wurde.
In einer Quelle aus dem 7. Jahrhundert wird berichtet: Wenn man einen Kreis mit Durchmesser 10 000 000 chang betrachtet, dann weiß man seit den Berechnungen von Zu Chongzhi, dass der Umfang dieses Kreises mehr als 31 415 926 chang beträgt und weniger als 31 415 927 chang (1 chang \(\approx\) 3,58 Meter).
Bei seinen Berechnungen von \(\pi\) geht Zu Chongzhi vom regelmäßigen Sechseck aus, dessen Umfang dreimal so groß ist wie der Durchmesser (Länge der längeren Diagonalen); dann wird die Anzahl der Ecken schrittweise verdoppelt.
Zwischen den Seitenlängen \(s_n\) eines regelmäßigen \(n\)-Ecks und \(s_{2n}\) eines regelmäßigen \(2n\)-Ecks besteht folgender Zusammenhang: Bezeichnet man den Abstand des Mittelpunkts von der Seite des \(n\)-Ecks mit \(x\), dann gilt:
- \(s_{2n}^2 = 2r \cdot (r–x)\) – nach dem Satz des Euklid,
- \(r^2=\frac{s_n^2}{4} + x^2\) – nach dem Satz des Pythagoras,
- also \(x= \sqrt{r^2–\frac{s_n^2}{4}}\) und damit \(s_{2n}=\sqrt{2r^2–r\cdot\sqrt{4r^2–s_n^2}}\)
- Mit \(r = 1\) erhält man dann schrittweise: \(s_{12}=\sqrt{2–\sqrt{4–1^2}}, s_{24}=\sqrt{2–\sqrt{4–(\sqrt{2–\sqrt{3}} )^2 }}\), \(=\sqrt{2 –\sqrt{2+\sqrt{3}}}\),...
Bereits Archimedes hatte bewiesen, dass ein Kreis den gleichen Flächeninhalt hat wie ein Rechteck mit den Seiten »halber Kreisdurchmesser« und »halber Kreisumfang«. Definiert man die Kreiszahl \(\pi\) als das Verhältnis von Umfang eines Kreises zum Durchmesser, dann ist \(\pi\) näherungsweise gleich dem halben Umfang eines regelmäßigen \(n\)-Ecks im Einheitskreis. Um die Genauigkeit von 7 Dezimalstellen zu erreichen, muss Zu Chongzhi – ohne die Hilfsmittel, die uns heute zur Verfügung stehen – die Seitenlänge eines regelmäßigen 24 576-Ecks berechnet haben – eine aus heutiger Sicht unglaubliche Rechenleistung!
Zu den besonderen Leistungen von Vater Zu Chongzhi und Sohn Zu Geng zählt auch die Herleitung einer exakten Volumenformel für die Kugel: Während es noch 200 Jahre vorher bei Liu Hui (220–280) heißt: Verdoppelt man das Volumen dieses Körpers und zieht hieraus die dritte Wurzel, dann erhält man den Durchmesser der Kugel (hier wird also mit \(\pi = 3\) gerechnet), geben Vater und Sohn als Formel für das Kugelvolumen \(V = \frac{11}{21} \cdot d^3\) an (rechnen also mit \(\pi = \frac{22}{7}\)).
Für die Herleitung benutzen sie den Grundsatz: »Die Volumina zweier Körper der gleichen Höhe stehen in einem festen Zahlenverhältnis, wenn die Größen der Schnittflächen beider Körper in gleicher Höhe in diesem Zahlenverhältnis stehen« – dies ist eine Verallgemeinerung eines Prinzips, das in Europa erst 1000 Jahre später von Bonaventura Cavalieri (1598–1647) formuliert wird.
Konkret zerlegen sie einen Würfel zunächst in acht kleinere, gleich große Würfel. Die kleineren Würfel wiederum zerlegen sie durch mehrere zylinderförmige Schnitte in vier kleinere Stücke, die sie nach dem oben angegeben Prinzip mit Teilen einer Kugel vergleichen, und bestimmen so deren Volumen. Bedeutsam erscheint vor allem, dass Zu Chongzhi und Zu Geng den Zusammenhang zwischen der Bestimmung der Fläche beim Kreis und des Volumens bei der Kugel erkannt haben.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.