Freistetters Formelwelt: Die normalsten Zahlen der Welt
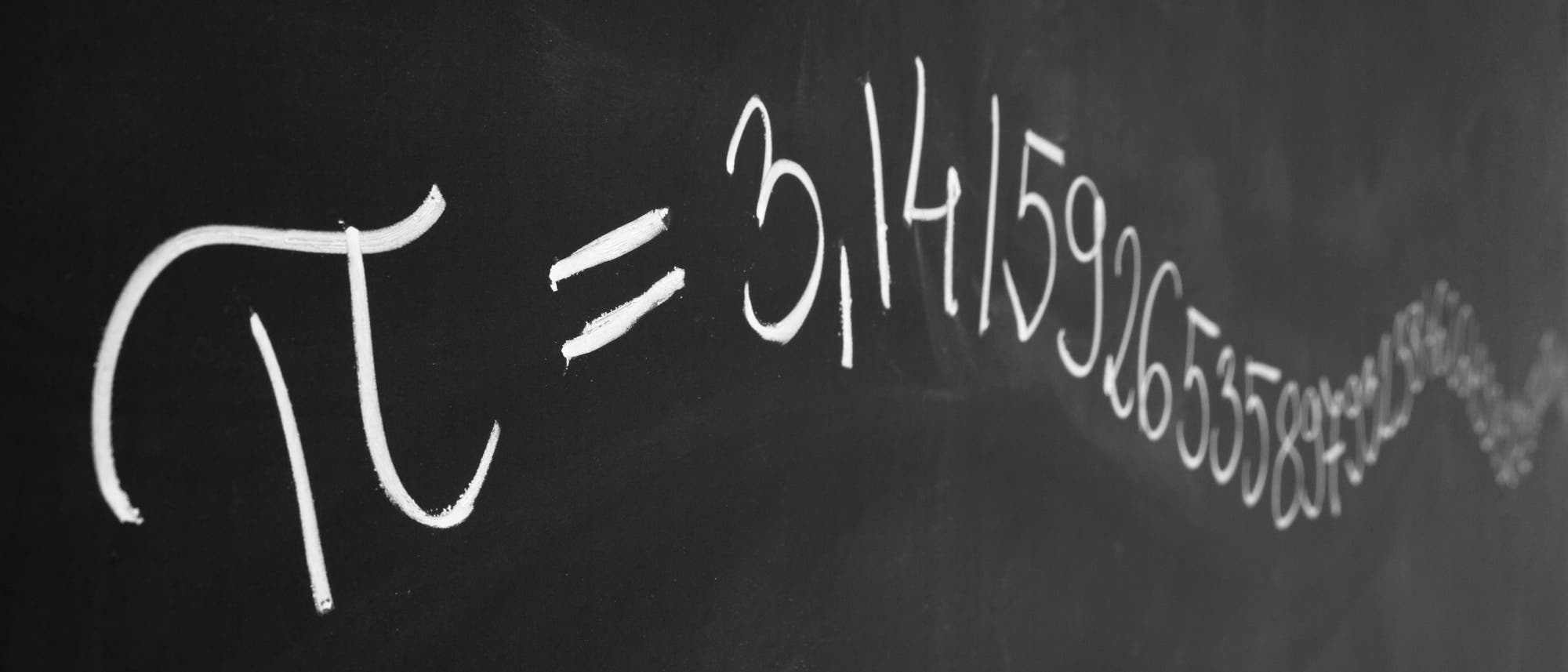
Die Sprache der Mathematik basiert auf der Logik. Normalerweise kann man sie nicht missverstehen – manchmal habe ich aber das Gefühl, dass die Wahl der Bezeichnungen ein wenig besser sein könnte. Zum Beispiel bei der "Normalität". Wenn man von "normalen Zahlen" spricht, dann denkt man im ersten Moment an das, was wir im Alltag unter "normal" verstehen. Normale Zahlen – das müssen Zahlen wie 1, 19 oder 47 sein. Zahlen, die nicht sonderlich außergewöhnlich oder kompliziert sind; eben normal.
Das was die Mathematik unter "normal" versteht, ist aber eher das genaue Gegenteil. Nämlich eine Zahl die diese Bedingung erfüllt:
Das sieht kompliziert aus und so gar nicht normal. Die Definition bezieht sich auf die Nachkommastellen einer reellen Zahl, die man zu beliebig langen Zifferngruppen zusammenfassen kann. Die ersten zehn Nachkommastellen der berühmten Kreiszahl Pi lauten zum Beispiel: π=3,1415926535. Dort findet man die Ziffernblöcke "1", "4", "5", "9", "2", "6" und "3" (die "1" und "5" tauchen mehrmals auf). Aber auch die zweistelligen Blöcke "14", "41", "15" und so weiter. Es gibt dreistellige Blöcke wie "141" oder "535", und natürlich auch den zehnstelligen Block "1415926535".
Zählt man nun, wie viele k-stellige Ziffernblöcke Bk es unter den ersten n Nachkommastellen der Zahl gibt, dann erhält man das, was in der Definition mit N(Bk,n) bezeichnet wird. Die Formel sagt dann nichts anderes, als das man unendliche, viele Nachkommastellen betrachten, alle k-stelligen Ziffernblöcke abzählen und das Ergebnis jeweils mit dem Quotient 1/bk vergleichen soll. b ist hierbei die Basis, in der die Zahl dargestellt wird – im Fall von Pi also 10, weil wir sie im Dezimalsystem aufgeschrieben haben.
Die Definition ist (für b=10) genau dann erfüllt, wenn man eine konkrete einzelne Ziffer (zum Beispiel "5") bei der Wahl eines beliebigen einstelligen Ziffernblocks aus den Nachkommastellen der Zahl in einem Zehntel aller Fälle findet. Eine bestimmte Abfolge aus zwei Ziffern sollte man in einem Hundertstel aller Fälle finden; einen Block aus drei Ziffern in einem Tausendstel aller Fälle, und so weiter.
So eine Zahl wird "normal" genannt. Obwohl daran eigentlich so gar nichts normal (zumindest im alltäglichen Sinn) ist. Denn wenn eine Zahl auf diese mathematische Weise normal ist, dann bedeutet das auch, dass man jede beliebige und beliebig lange Abfolge von Ziffern mit Sicherheit irgendwo in der Entwicklung der Nachkommastellen antrifft. Mein Geburtstag zum Beispiel ist am 28. Juli 1977. Den Ziffernblock "28071977" würde ich daher in einer normalen Zahl nicht nur mit Sicherheit irgendwo entdecken können, ich würde ihn sogar unendlich oft finden (und zwar in einem hundert Millionstel aller Fälle bei der Betrachtung eines beliebigen achtstelligen Ziffernblocks). Tatsächlich taucht diese Kombination an der 52 126 615te Nachkommastelle von Pi auf, und insgesamt viermal unter den ersten 200 Millionen Nachkommastellen.
Ob die Zahl Pi allerdings tatsächlich normal ist, konnte noch nicht bewiesen werden. Es sieht alles danach aus, aber ohne exakten Beweis kann man sich in der Mathematik nie sicher sein. Mit Sicherheit normal ist dagegen die so genannte Champernowne-Zahl C. Sie wurde 1933 vom englischen Mathematikstudenten David Champernowne entdeckt und war die erste Zahl, deren Normalität nachgewiesen werden konnte. Im Dezimalsystem konstruiert man sie einfach dadurch, dass man die natürlichen Zahlen als Nachkommastellen hintereinander schreibt:
C= 0,123456789101112131415161718192021...
Und da diese Zahl zweifelsfrei normal ist, findet sich dort nicht nur jeder beliebige Geburtstag, sondern jede nur vorstellbare durch Zahlen kodierbare Information. Und jede nicht vorstellbare Information ebenfalls. Jedes Buch zum Beispiel, das jemals geschrieben wurde und auch all die, die (noch) nicht geschrieben wurden. Und das ist definitiv nicht normal!
Schreiben Sie uns!
2 Beiträge anzeigen