Freistetters Formelwelt: Wo findet man Primzahlen?
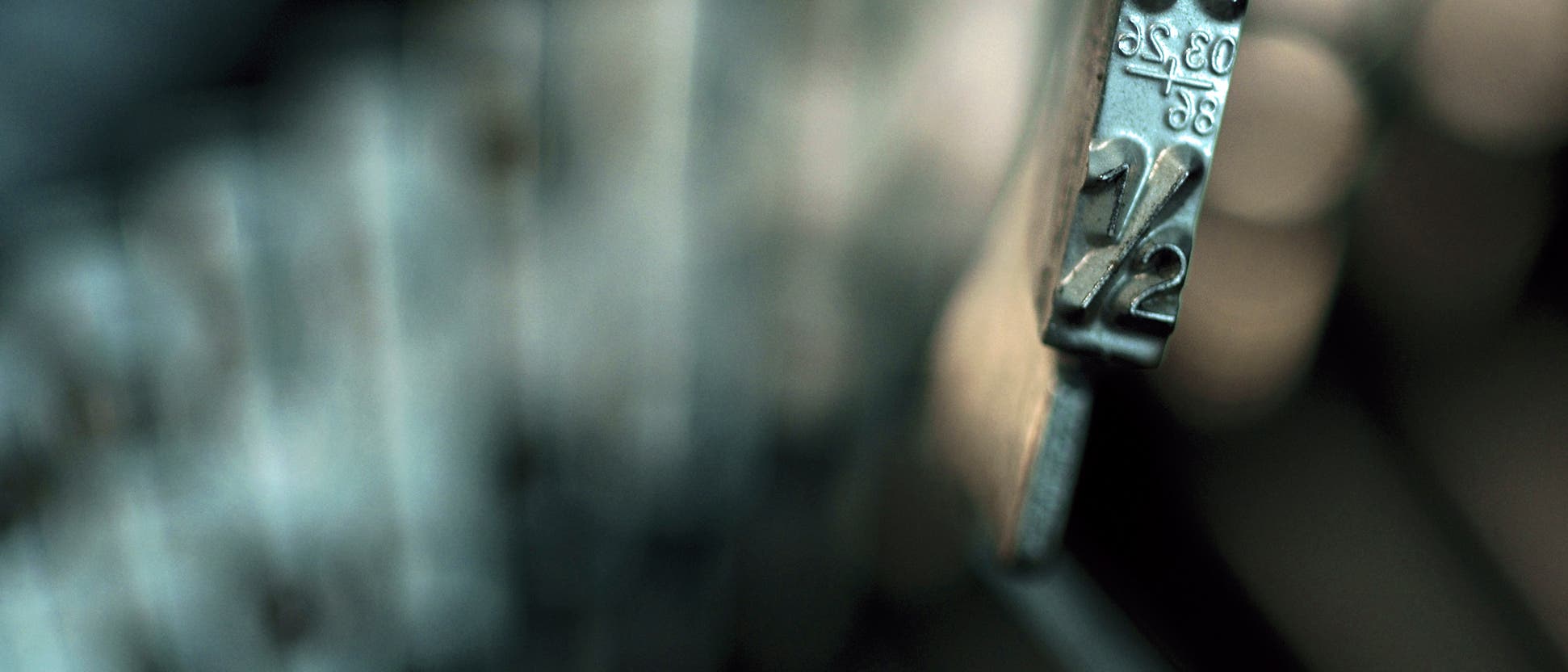
Wissenschaft wird immer dann besonders spannend, wenn komplett unterschiedliche Disziplinen auf einmal Gemeinsamkeiten entdecken. Wenn zum Beispiel die Untersuchung der kleinsten Bausteine der Materie etwas über den Beginn des Universums aussagen kann. Oder Quantenmechanik plötzlich eine wichtige Rolle in der Biologie spielt. Auch in der Mathematik tauchen immer wieder unerwartete Verbindungen zwischen verschiedenen Forschungsfeldern auf.
Zum Beispiel bei dieser berühmten mathematischen Funktion:
Das ist die riemannsche ζ-Funktion ("Zeta-Funktion"), und sie sieht eigentlich recht unscheinbar aus. Würde man zum Beispiel für s die Zahl 2 einsetzen, dann ergibt sich ζ(2)=1+1/4+1/9+1/16+…. Das Ergebnis dieser unendlichen Addition wurde schon 1735 durch Leonhard Euler auf π2/6 bestimmt.
Als riemannsche ζ-Funktion ist die Gleichung aber für komplexe Zahlen definiert (Zahlen, die aus einem "Realteil" und einem "Imaginärteil" zusammengesetzt sind), deren Realteil größer als 1 sein muss. 1859 hat der deutsche Mathematiker Bernhard Riemann eine sehr überraschende Verbindung zwischen dieser aus dem damals jungen Gebiet der komplexen Funktionentheorie stammenden Gleichung und der seit der Antike betriebenen Zahlentheorie hergestellt.
Dabei geht es um Nullstellen der ζ-Funktion. So wird ζ(s) gleich null, wenn s eine negative gerade ganze Zahl ist. Das war Riemann bereits bekannt. Ihm ging es um die restlichen, also die so genannten nichttrivialen Nullstellen der Funktion. Er vermutete, dass sie alle komplexe Zahlen mit einem Realteil gleich ½ sein müssen.
Das ist die bis heute unbewiesene riemannsche Vermutung. Könnte man sie beweisen, hätte das dramatische Auswirkungen für unser Verständnis der Primzahlen. Trotz jahrtausendelanger Beschäftigung mit ihnen hat bis jetzt immer noch niemand ein mathematisches Gesetz gefunden, das erklärt, nach welchen Gesetzmäßigkeiten diese Zahlen auftauchen.
Wenn wir uns die natürlichen Zahlen entlang einer Geraden aufgereiht vorstellen, dann gibt es keine Formel, die uns sagt, wie weit wir diese Gerade ausgehend von einer Primzahl entlanggehen müssen, um auf die nächste Primzahl zu treffen. Riemann konnte diese Frage mit der ζ-Funktion von einer eindimensionalen Gerade auf eine zweidimensionale Ebene übertragen (aufgespannt durch Real- und Imaginärteil der komplexen Zahlen). Stellt man sich die ζ-Funktion als Landschaft auf dieser Ebene vor, sind die Nullstellen jene Punkte, die genau auf Meeresniveau liegen. Riemann behauptete nun, dass ein Zusammenhang zwischen der Verteilung der Nullstellen und der Verteilung der Primzahlen besteht. Wüsste man, wo all die unendlich vielen Nullstellen liegen, könnte man daraus ein Muster für das Auftreten der Primzahlen bestimmen.
Riemann vermutete, dass die Nullstellen nicht beliebig in der Landschaft verteilt sind, sondern sich alle entlang einer Linie in der Ebene aufreihen (nichts anderes bedeutet die Aussage "ihr Realteil muss gleich ½ sein" geometrisch). Er konnte es aber nicht beweisen, ebenso wenig wie seine Nachfolger. Die riemannsche Vermutung gehört zu den bedeutendsten ungelösten Problemen der Mathematik, und auf den Fund eines gültigen Beweises ist ein Preisgeld von einer Million Dollar ausgesetzt.
Die unerwartete Verbindung zwischen Funktionentheorie und Zahlentheorie stellt Mathematiker seit mehr als 150 Jahren vor ein Rätsel. Vielleicht hilft ja nun ein weiterer Austausch zwischen den Disziplinen: Schon im letzten Jahrhundert war Forschern aufgefallen, dass mathematische Methoden aus der Quantenmechanik den Beweis der riemannschen Vermutung liefern könnten. Entsprechende Versuche waren viel versprechend, aber leider noch nicht erfolgreich. Vermutlich braucht es noch ein wenig mehr Interdisziplinarität, um das Rätsel endgültig zu lösen.
Schreiben Sie uns!
1 Beitrag anzeigen