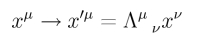Die Lorentz-Transformation ist eine mathematische Operation, die zwischen gegeneinander gleichförmig geradlinig bewegten Bezugssystemen (Spezielle Relativitätstheorie, SRT) oder gegeneinander frei fallenden (beschleunigten) Bezugssystemen (Allgemeine Relativitätstheorie) vermittelt. Sie hat die klassische Galilei-Transformation abgelöst, in der die Zeittransformation eine Identität war, t = t', und somit den Begriff einer absolutenZeit erlaubte. In der Relativitätstheorie hat die Zeit einen relativen Charakter, was sehr gut aus den Gleichungen der Lorentz-Transformation zu ersehen ist.

Mathematisch formuliert

Mathematisch gesehen ist die Lorentz-Transformation eine lineare, homogene Transformation (siehe erste Abbildung rechts oben), die bezogen auf zu transformierenden Vierervektoren der Relativitätstheorie durch eine 4 × 4-Matrix (meist mit Λ bezeichnet, siehe Gleichung) dargestellt werden kann. Die Lorentz-Transformation ist ein Spezialfall der Poincaré-Transformation. Letztere bezieht ebenfalls Translationen mit ein und ist damit eine lineare, inhomogene Transformation. Beide Transformationstypen bilden mathematische Gruppen: die Lorentzgruppe bzw. die Poincarégruppe.

Der Pionier

Die Bezeichnung Lorentz-Transformation ist mit dem niederländischen Physiker Hendrik Antoon Lorentz (1853 – 1928) verbunden, der grundlegende Arbeiten auf dem Gebiet der Relativitätstheorie leistete und – wie Albert Einstein – den negativen Ausgang des Michelson-Morley-Versuchs zur Messung eines Weltäthers aufgriff. Mit ihm sind bis heute die Begriffe Lorentz-Kontraktion, Lorentz-Faktor und Lorentzgruppe verknüpft.

absolute Lichtgeschwindigkeit

Die natürliche und einzige Einheit der Speziellen Relativitätstheorie ist die Vakuumlichtgeschwindigkeit c. Sie ist unveränderlich in jedem Bezugsystem und in diesem Sinne absolut wie in der SRT postuliert wird (Nicht alles ist relativ in der Relativitätstheorie!). Es bietet sich daher an, Geschwindigkeiten in Einheiten der Lichtgeschwindigkeit zu messen. Dies legt die dimensionslose Größe v/c (meist als β bezeichnet) fest, wie die 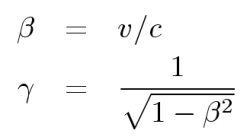zweite Abbildung zeigt. In der Ableitung des Lorentz-Transformationsgesetzes taucht der so genannte Lorentz-Faktor (γ, siehe zweite Abbildung, untere Zeile) auf. Dieser Faktor, der von der Relativgeschwindigkeit v zweier gegeneinander bewegter Bezugssysteme abhängt, ist immer zu beachten, wenn man von einem Bezugssystem ins andere wechselt. Er ist von immenser Wichtigkeit für die gesamte Relativitätstheorie und ist derjenige Faktor, der die Längen- oder Lorentz-Kontraktion und die Zeitdilatation ausmacht.
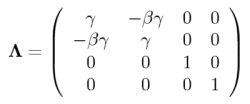Mathematisch kann man die Lorentz-Transformation durch ein Matrix-Vektor-Produkt schreiben (erste Gleichung oben). Die Vektoren x sind Vierervektoren mit einer zeitlichen Komponente und drei räumlichen Komponenten. Entsprechend ist die Transformationsmatrix, die gerade die Lorentz-Transformation vermittelt, eine 4 × 4-Matrix, hat also 16 Einträge. Links ist die Transformationsmatrix dargestellt für eine Lorentz-Transformation in x-Richtung, einem so genannten x Boost.
Anschaulich ist die Spezielle Lorentz-Transformation eine Drehung im Minkowski-Raum. Die Lorentzgruppe ist verwandt mit der Drehgruppe und enthält die Rotationen im Raum. Ein Boost ist im Prinzip auch eine Drehung, in der allerdings Raum und Zeit ineinander überführt werden (das wird klar beim Betrachten der expliziten Transformationsgesetze unten). Deshalb nennt man die Boosts auch Pseudo-Rotationen. Die Allgemeine Lorentz-Transformation entspricht hingegen einer Speziellen Lorentz-Transformation verkettet mit einer Raumdrehung.
Anschaulich bedeutet dies, dass die Relativgeschwindigkeitv zwischen ungestrichenem (Ruhesystem) und gestrichenem System (relativ bewegtes System) parallel zur x-Richtung ist. Wie die nächste Abbildung rechts zeigt, bleiben die y- und z-Komponente des Orts-Vierervektors unverändert (invariant), während sich die Raumkomponente in Boost-Richtung (nämlich x) und die zeitliche Komponente t verändern, wenn man in ein anderes Bezugssystem wechselt! Diese Eigenschaft belegt die enge Verknüpfung von Raum und Zeit zur Raumzeit bzw. dem Raum-Zeit-Kontinuum. Nachrechnen kann man die vier komponentenweise notierten Transformationsgesetze schnell durch Berechnung des Matrix-Vektor-Produkts aus der Transformationsmatrix oben und einem Orts-Vierervektor x = (x₀, x₁, x₂, x₃)^T = (ct, x, y, z)^T (Bemerkung: ^T steht für den transponierten Vektor, denn: Matrix × Spaltenvektor = Spaltenvektor.).

Weitere Anmerkung

Es gibt auch Schreibweisen der Lorentz-Transformation, bei denen die imaginäre Einheiti = (-1)^1/2 verwendet wird. Diese Zugänge sind zwar mathematisch äquivalent, jedoch veraltet. Ein Gebrauch von i ist aus pädagogischen Gründen nicht zu empfehlen, weil es vor allem Einsteiger in der Relativitätstheorie verwirrt.

Eigenschaften der Lorentz-Transformation

• Es ist eine lineare Transformation. Durch diese Eigenschaft bleibt physikalisch gesprochen der Typus der Bewegung (gleichförmig bzw. frei fallend) erhalten.
• Die Determinante der Transformationsmatrix ist 1 (siehe kurze Rechnung unten).
• Für den Limes kleiner Geschwindigkeiten gegenüber der Vakuumlichtgeschwindigkeit c geht die Lorentz-Transformation in die klassische Galilei-Transformation über.
• Die inverse Lorentz-Transformation erhält man durch Ersetzen von v/c (beta) in der Transformationsmatrix durch -v/c. Physikalisch interpretiert wird dabei einfach die Bewegungsrichtung umgekehrt.

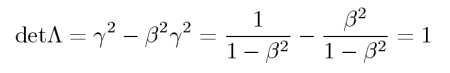
Lorentz-Invarianten

Lorentz-Invarianten ändern sich nicht bei einer Lorentz-Transformation, d.h. sie sind in allen Bezugssystemen gleich! So ist die Länge eines Weltvektors eine Lorentz-Invariante, weil Weltvektoren unter Lorentz-Transformationen nur im Minkowski-Raum gedreht werden. Dies enthüllt den engen Zusammenhang von Rotationsgruppen und der Speziellen Lorentzgruppe.

Additionstheorem für Geschwindigkeiten

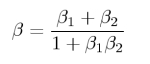Das Additionstheorem für (Relativ-)Geschwindigkeiten lässt sich leicht durch eine Verkettung von Lorentz-Transformationen nachweisen. An diesem Gesetz (siehe Gleichung rechts) sieht man leicht, dass das Licht einer bewegten Lichtquelle sich nicht etwa mit Lichtgeschwindigkeit plus Geschwindigkeit der Lichtquelle bewegt, sondern – wie im Postulat Einsteins gefordert – die Lichtgeschwindigkeit konstant bleibt. Dieses Additionstheorem geht für kleine Geschwindigkeiten (v viel kleiner als c) in das wohl vertraute Gesetz für Geschwindigkeiten über, wonach ein Geschoss, das von einer bewegten Quelle stammt, auch die Geschwindigkeit der Quelle hinzuaddiert bekommt.

Spinoren

Eine verallgemeinerte Mathematik der Lorentz-Transformation in der Allgemeinen Relativitätstheorie bietet die Spinor-Algebra.