Fehlerrechnung

Walter Seibt, Gießen

1. Einleitung

Unvermeidbarkeit von Meßfehlern

Jede reale Messung einer physikalischen Größe ist mit einer Unsicherheit im Ergebnis behaftet. Dies ist eng mit der Frage verknüpft, ob es den wahren WertX einer physikalischen Größe, der letztendlich ja doch ermittelt werden soll, überhaupt gibt. Im allgemeinen muß diese Frage wohl verneint werden, da der wahre Wert einer stetigen Variablen nie genau bestimmt werden kann. Wir wollen für unsere Darstellung jedoch an diesem Begriff festhalten und definieren ihn als den Mittelwert einer unendlich langen Meßreihe. Er kann daher im Experiment nie tatsächlich ermittelt werden, die Messung liefert stets nur einen Bestwertx_Best.

Auch der Begriff des Fehlersδx sollte geklärt werden. Ein Fehler in unserem Zusammenhang ist nicht das Ergebnis eines Fehlverhaltens des Messenden, sondern es handelt sich um die prinzipiell unvermeidliche Meßunsicherheit, die jeder Messung auch bei größter Sorgfalt anhaftet. Da sich dieser Begriff jedoch eingebürgert hat, wollen wir auch an ihm festhalten.

Die Angabe eines Meßergebnisses erfolgt daher stets in der Form: wahrer Wert = Bestwert ± Fehler, oderX = x_Best ± δx.

Bedeutung der Fehlerabschätzung

Hinter jeder Messung steckt eine gewisse Absicht. Die Größe des Fehlers entscheidet oft darüber, ob eine Messung ihren Zweck erfüllt oder nicht.

Viele Messungen dienen etwa dazu, die Vorhersagen einer Theorie zu überprüfen. Berühmtestes Beispiel eines Experimentes dieser Art war die Messung der Ablenkung eines Lichtstrahls, der nahe an der Sonne vorbeigeht. Auf Grund seiner Allgemeinen Relativitätstheorie sagte Einstein 1916 einen Winkel von α = 1,8″ voraus. Eine Messung im Jahre 1919 (von Eddington et al.) lieferte einen Wert von α = 2,0″ ± 0,3″. Dieses Ergebnis bestätigt mit hoher Wahrscheinlichkeit die Vorhersage und damit auch die Theorie. Ein Ergebnis von α = 0″, wie es klassisch erwartet wird, liegt weit außerhalb der ermittelten Fehlergrenzen (siehe Randspalte). Wäre der Fehler der Messung wesentlich größer oder völlig unbekannt, könnte keine Entscheidung über die Gültigkeit von Einsteins Theorie getroffen werden.

Einstein wies 1916 darauf hin, daß nach der Allgemeinen Relativitätstheorie Licht, das nahe an der Sonne vorbeigeht, um einen Winkel α = 1,8′ abgelenkt wird. Gemäß der vorrelativistischen Physik wird α = 0 erwartet, die Berücksichtigung der Speziellen Relativitätstheorie führt zur Vorhersage α = 0,9′. Auch dieser Wert liegt außerhalb der Fehlergrenzen der Messung von 1919.

2. Grundbegriffe

Systematischer und zufälliger Fehler

Systematische Fehler, herrührend von Unzulänglichkeiten der Meßgeräte, verfälschen ein Meßergebnis stets um den gleichen Betrag in die gleiche Richtung. Ihnen kommt man durch eine Wiederholung der Messung nicht auf die Spur, und sie können auch durch Rechenaufwand nicht verringert werden. Sie müssen auf andere Weise ermittelt und apparativ beseitigt werden.

Im Gegensatz dazu kann der statistische oder zufällige Fehler (zufällige Unsicherheit) das Ergebnis in beide Richtungen verändern. Er hat seine Ursache im Beobachter selbst. Er ist prinzipiell unvermeidbar, kann jedoch durch wiederholte Messungen und geeignete Auswertungsmethoden in seiner Größe abgeschätzt werden.

Relativer und absoluter Fehler

Die Angabe der Meßunsicherheit kann auf zwei verschiedene Weisen erfolgen:

Wird die Meßunsicherheit als Zahlenwert δx (mit der gleichen Einheit wie die Meßgröße selbst) angegeben, dann spricht man vom absoluten Fehler.

Man kann die Qualität einer Messung aber auch durch den Quotienten aus δx und x_Best anzeigen. Diesen Ausdruck bezeichnet man als relativen Fehler (relative Unsicherheit):

.

Diese dimensionslose Größe gibt die Größe der Meßunsicherheit (nach Multiplikation mit 100) in Prozent an.

Signifikante Stellen und Fehlerangabe

Das Hauptanliegen der Fehlerrechnung ist es, nach praktischen Verfahren zu suchen, die es erlauben, eine quantitative Aussage über die Größe der Meßunsicherheit δx zu machen. Man muß sich jedoch darüber im klaren sein, daß es exakte Fehlerangaben nie geben kann. Was eine Fehlerrechnung mit ihren anerkannten Methoden leisten kann, sind Angaben darüber, mit welcher Wahrscheinlichkeit man bei einer identisch wiederholten Meßreihe ein Ergebnis innerhalb bestimmter Grenzen erwarten kann.

Unter diesem Aspekt sollte man auch bei der Formulierung eines Meßergebnisses zunächst nur die Stellen angeben, in denen sich der Fehler mit großer Wahrscheinlichkeit noch nicht auswirkt (signifikante Stellen), plus eine weitere Stelle, die auf Grund der Fehlerrechnung unsicher ist. Da der Fehler selbst ebenfalls mit einer hohen Unsicherheit belastet ist, genügt dort im allgemeinen die Angabe einer, maximal zwei Stellen.

3. Messung einer Variablen

Um die Zuverlässigkeit einer Messung der Größe x abschätzen zu können, führen wir sie mehrmals durch und unterziehen die so gewonnen Meßdaten einer statistischen Analyse (statistische Unsicherheit).

Statistische Betrachtungen

Mittelwert

Es kann gezeigt werden, daß der (arithmetische) Mittelwert

, der aus den Einzelwerten x_i gewonnen werden kann, einen Bestwert x_Best für die Meßgröße X darstellt:

.
Standardabweichung der Einzelmessung

Um einen Schätzwert für die mittlere Unsicherheit der Meßwerte zu finden, bildet man die sogenannte Standardabweichungder Einzelmessungσ_x aus den einzelnen Werten und dem Mittelwert. Diese Größe hängt nur von der Qualität der Meßapparatur ab, nicht jedoch von der Anzahl der durchgeführten Messungen:

.
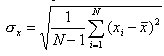
Standardabweichung des Mittelwertes

Naturgemäß hat man in den Mittelwert einer Meßreihe ein größeres Vertrauen als in die einzelnen Meßwerte. Man verwendet daher die Standardabweichung für den Mittelwert

als quantitatives Maß für die Meßunsicherheit δx:

.

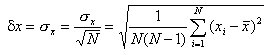
Ein Meßergebnis für die Größe x hat daher folgendes Aussehen:

.

Im folgenden soll versucht werden, zu begründen, daß der Mittelwert einer Meßreihe als Bestwert für die gesuchte Größe verwendet werden kann und daß die Standardabweichung des Mittelwertes eine Größe darstellt, die eine quantitative Aussage über den Fehler ermöglicht.

Darstellung der Meßergebnisse

Um dieses Ziel zu erreichen, müssen statistische Verfahren in Anwendung kommen. Dazu ist es erforderlich, die Daten einer umfangreichen Meßreihe in passender Form darzustellen. Eine einfache Möglichkeit bieten Stabdiagramme.
Stabdiagramme

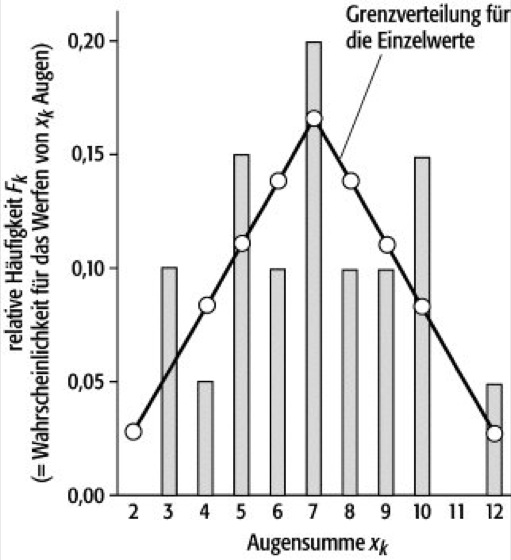
Die Darstellung in einem Stabdiagramm eignet sich besonders, wenn nur diskrete Ergebniswerte auftreten (wie z.B. bei Würfelexperimenten oder anderen Zählexperimenten, bei denen nur die Häufigkeit eines Ereignisses gefragt ist). Es wird die relative Häufigkeit eines Ergebnisses gegen den Meßwert als senkrechter Balken aufgetragen ( Abb. 1 ).

Zunächst soll an einem Würfelexperiment das Verfahren erläutert werden, da in diesem Fall die Wahrscheinlichkeiten für das Eintreten der einzelnen Ergebnisse bekannt sind und deshalb der Mittelwert einer unendlich langen Meßreihe
(= wahrer Wert = Erwartungswert) berechnet werden kann.

Das Beispiel zeigt im linken Diagramm die beim Wurf mit zwei Würfeln bei N = 20 Würfen erzielten Augenzahlen. Die eingezeichnete Linie ist die berechnete Wahrscheinlichkeit. Sie ist gleich der bei unendlich vielen Versuchen erzielten Häufigkeitverteilung (= Grenzverteilung für die Einzelmessung).

Errechnet man Mittelwert und Standardabweichung für den Mittelwert, dann erhält man als Ergebnis für die dargestellte Meßreihe(Meßwert für x) = 7,05 ± 0,54.

Der wahre Wert X beträgt hier 7,0.

Der obere Teil von Abb. 1 zeigt die Verteilung der Mittelwerte, wenn man die Meßreihe oft wiederholt. Würde man die gleiche Meßreihe unendlich oft durchführen, dann würden die Ergebnisse, nach ihrer Häufigkeit sortiert, das Dreieck (die Grenzverteilung für den Mittelwert) füllen. Das Flächenverhältnis des schraffierten Teils zur Gesamtfläche gibt also die Wahrscheinlichkeit an, mit der eine erneut durchgeführte Messung innerhalb der angegebenen Fehlergrenzen liegt, in unserem Fall sind das ca. 64,4 %. Damit haben wir ein Verfahren kennengelernt, das eine quantitative Aussage bezüglich des Fehlers erlaubt.

Voraussetzung dafür ist jedoch, wie hier gezeigt wurde, die Kenntnis der Grenzverteilung. Wenn es uns gelingt, für reale physikalische Meßreihen die Grenzverteilung mathematisch zu formulieren, dann haben wir unser Ziel erreicht.
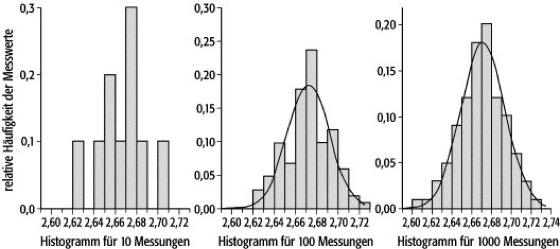
Histogramm

In den meisten Fällen liefert eine Messung keine ganzzahligen Ergebnisse, da die meisten physikalischen Größen einen kontinuierlichen Bereich möglicher Werte haben. Man teilt dann den Wertebereich in eine geeignete Anzahl von Intervallen oder Klassen ein und zählt jeweils, wieviele Ergebniswerte in eine solche Klasse fallen (Histogramm). Als Beispiel wurden in Abb. 2 die Messungen einer Zeit von ca. 2,67 s (Meßgenauigkeit 0,001 s, Klassenbreite 0,01 s) dargestellt. Man erkennt qualitativ, daß die zu erwartende Verteilung bei einer Steigerung der Anzahl der Messungen durch eine symmetrische Glockenkurve wiedergegeben wird, wie sie in der Abbildung bereits andeutungsweise eingetragen ist.
Grenzverteilungen

Die Verteilungskurve der Meßresultate für den Grenzfall unendlich vieler Messungen nennt man die Grenzverteilung dieser Messung.

Wenn die Grenzverteilung f(x) explizit bekannt ist, dann kann daraus der Mittelwert und die Standardabweichung errechnet werden:

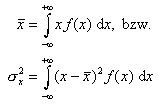
Verteilungen

Wir stehen nun vor der Frage, ob es möglich ist, die Grenzverteilung für ein bestimmtes Experiment vorauszusagen. Man kann zeigen, daß in den meisten Fällen als Grenzverteilung die sogenannte Normalverteilung (Gauß-Verteilung, normale Dichtefunktion) angenommen werden kann. Zu Erklärung dieses Zusammenhanges geht man von der sog. Binomialverteilung für die Ereignisse aus.
Binomialverteilung

Diese Verteilung ist anwendbar, wenn mit vielen identischen Objekten das gleiche Experiment durchgeführt wird, wobei für jedes Objekt ein bestimmtes Ergebnis mit der Wahrscheinlichkeit p möglich ist. Wird mit n Teilchen das gleiche Experiment gemacht, dann ist die Wahrscheinlichkeit dafür, daß bei ν Teilchen das Ereignis beobachtet wird,

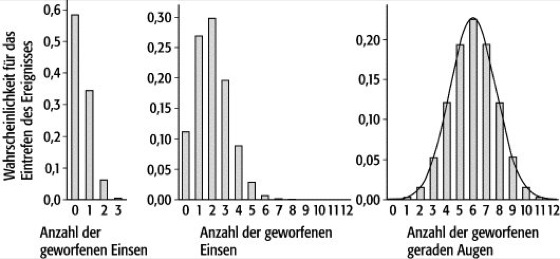
In Abb. 3 werden die Verteilungen für die folgenden Experimente dargestellt:
• Wahrscheinlichkeit, beim Werfen von drei Würfeln eine bestimmte Anzahl von Einsen zu erhalten (Mittelwert = 1/2)
• Wahrscheinlichkeit, beim Werfen von zwölf Würfeln eine bestimmte Anzahl von Einsen zu erhalten (Mittelwert = 2)
• Wahrscheinlichkeit, beim Werfen von zwölf Würfeln eine bestimmte Anzahl gerader Augen zu erhalten (Mittelwert = 6).

Man erkennt, daß mit steigendem Mittelwert auch diese Verteilung die Form einer symmetrischen Glockenkurve annimmt. Es kann gezeigt werden, daß für diesen Grenzfall die Binomialverteilung in die sogenannte Gauß-Verteilung oder Normalverteilungf_X,σ(x) übergeht.
Poisson-Verteilung

Auch die Poisson-Verteilung kann für den Fall großer Objektzahlen durch die Normalverteilung f_X,σ(x) beschrieben werden.
Normal- oder Gauß-Verteilung

Bei dieser Funktion handelt es sich um eine Glockenkurve, die durch zwei Parameter charakterisiert ist: Sie ist beim Wert X (dem wahren Wert) zentriert und besitzt am Wendepunkt die Breite 2σ (Breitenparameter).

Sie hat das in Abb. 4 dargestellte Aussehen und gehorcht der folgenden Funktion:

Wenn es uns gelingt, zu zeigen, daß die Werte einer Meßreihe, die unabhängig und zufällig sind, durch die Binomialverteilung gegeben sind, dann haben wir unser Ziel erreicht.
Die Normalverteilung als Grenzverteilung bei Meßreihen

Unter der Annahme, daß bei der Messung einer Größe x, deren wahrer Wert X sei, n unabhängige Quellen zufälliger Abweichungen auftreten (unabhängige Unsicherheit), die der Einfachheit halber alle gleich groß sein sollen und mit gleicher Wahrscheinlichkeit den Meßwert vergrößern bzw. verkleinern sollen, dann läßt sich zeigen, daß die zu erwartenden Wahrscheinlichkeiten für die einzelnen Meßwerte durch die Binomialverteilung beschrieben werden (Random-Walk-Problem!), welche für großes n durch die Normalverteilung ersetzt werden kann. Damit erhalten wir die Möglichkeit, eine quantitative Aussage darüber zu machen, was bei dieser Verteilung die Angabe der Unsicherheitsgrenze σ bedeutet.

Wertet man das Integral

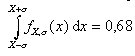
aus, dann sieht man, daß ca. 68 % aller Messungen (dies entspricht wiederum der gerasterten Fläche in der Abbildung) im Bereich dieser Unsicherheitsgrenzen liegen.

Fehlerfunktion

Man kann das Vertrauen, das in ein Meßergebnis gesetzt wird, dadurch vergrößern, daß man den möglichen Fehlerbereich auf den Wert t · σ erweitert. Mit welcher Wahrscheinlichkeit in diesem Fall eine erneute Messung innerhalb der Fehlergrenzen liegt, kann aus der sogenannten Gaußschen Fehlerfunktion (auch normales Fehlerintegral genannt) abgelesen werden.

Die Integralfunktion ( Abb. 5 ) zeigt die Wahrscheinlichkeit P, daß ein Ergebniswert von x innerhalb von t Standardabweichungen vom wahren Wert X fällt. Läßt man eine Unsicherheit von 2σ nach jeder Seite zu, dann liegen bereits ca. 95 % aller Messungen im Fehlerbereich.
Das Verwerfen von Daten

Mit Hilfe des Chauvenetschen Kriteriums kann beurteilt werden, ob ein etwas ausgefallener Wert innerhalb einer Meßreihe (ein sogenannter ›Ausreißer‹) bei der Mittelwertbildung berücksichtigt werden sollte, oder ob der Wert aus einem Experimentierfehler resultiert und deshalb verworfen werden muß.

Wir wollen annehmen, daß eine Meßreihe aus N Messungen einen Mittelwert von

und eine Standardabweichung von σ_x besitze. Wir wollen weiter annehmen, daß unter den Meßwerten ein verdächtiger Wert x_verd ist, der um (t_verd · σ_x) vom Mittelwert abweicht. Mit Hilfe der Integralfunktion kann man die Wahrscheinlichkeit P ausrechnen, mit der ein Meßwert außerhalb dieser Schranken fällt. Multipliziert man dieses P mit N, dann erhält man die Anzahl der Meßwerte, die im Mittel auf Grund der Normalverteilung außerhalb (t_verd · σ_x) fallen. Damit erhalten wir die erwartete Anzahl n von Meßwerten, die mindestens so schlecht wie x_verd sind:n(schlechter als x_verd) = N P (außerhalb t_verd · σ_x).

Wenn n kleiner als 1 / 2 ist, dann erfüllt x_verd das Chauvenetsche Kriterium nicht und wird verworfen. Auch dieses Kriterium ist wie alle anderen Aussagen der Fehlerrechnung nur eine Wahrscheinlichkeitsangabe und damit in ihrer Wertung einer subjektiven Beurteilung unterworfen.

Mittelwert als Bestwert

Es soll nun noch begründet werden, daß der Mittelwert einer Meßreihe tatsächlich als Bestwert für die gesuchte Größe interpretiert werden kann.

Die wahren Werte X und σ (aus einer unendlich langen Meßreihe ermittelt!) sind nicht bekannt. Um aus endlich vielen Daten einen Bestwert für diese Größen zu erhalten, wird das Prinzip der größten Wahrscheinlichkeit angewandt.

Wären die Parameter X und σ bekannt, dann könnten die Wahrscheinlichkeiten für die tatsächlich gemessenen Werte x_i berechnet werden. So ist z.B. die Wahrscheinlichkeit, den Wert x₁ zu messen, auf Grund der Normalverteilung proportional zum Ausdruck

.

Die Wahrscheinlichkeit, alle x_i der Meßreihe zu erhalten, ist das Produkt der Einzelwahrscheinlichkeiten:

In dieser Beziehung sind X und σ unbekannt. Als Bestwerte ermitteln wir diejenigen Werte dieser Größen, für welche die beobachteten x₁, x₂, 1/4, x_N am wahrscheinlichsten sind. P (als Funktion von X) ist maximal, wenn der Exponent minimal ist. Differenziert man diesen und setzt die Ableitung gleich null, dann erhält man

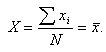
Der so definierte Bestwert X ist gleich dem Mittelwert der Meßreihe

. Nach dem gleichen Verfahren ergibt sich, daß der Bestwert für die Breite σ gleich der Standardabweichung der N beobachteten Werte x_i ist.

Mit anderen Worten: Für eine Normalverteilung, die am Mittelwert

zentriert ist und die Breite σ besitzt, ist die Wahrscheinlichkeit am größten, die real gemessene Ergebnisverteilung zu erhalten.
Der gewichtete Mittelwert

Oft ergibt sich die Aufgabe, mehrere unabhängige Messungen derselben physikalischen Größe x_1,x_2,1/4x_N zu einem Bestwert x_Best zu kombinieren, wobei die Messungen mit unterschiedlicher Genauigkeit σ₁, σ_2, 1/4, σ_N durchgeführt wurden. Auch hier hilft uns das Prinzip der größten Wahrscheinlichkeit weiter.

Der Bestwert für den unbekannten Wert X ist derjenige Wert, für den die tatsächlichen Beobachtungen x_A und x_B am wahrscheinlichsten sind. Im Exponenten der e-Funktion erscheint diesmal ein Term der Form

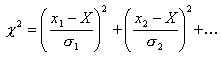
Wird differenziert und nach X aufgelöst, erhält man den folgenden gewichteten Mittelwert als Bestwert

,

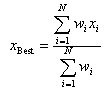
wobei die als Gewichte definierten Größen

benutzt wurden: Kleine Standardabweichung bedeutet großes Gewicht bei der Mittelung.

Der Chi-Quadrat-Test

Um zu testen, ob die Ergebnisse einer Meßreihe der zu erwartenden Grenzverteilung folgen, kann man den sogenannten Chi-Quadrat-Test oder χ²-Test durchführen.

Wir wollen annehmen, daß eine Größe x mehrmals gemessen wird, und es soll geprüft werden, ob die Werte einer bestimmten Verteilung f(x) folgen. Dazu teilen wir die Meßwerte in n Klassen ein (k = 1, ..., n) und ermitteln jeweils die Anzahl B_k der Beobachtungen, die in Klasse k fallen. Diese Zahlen vergleichen wir mit der auf Grund der als bekannt angenommenen Verteilung errechneten Anzahl von erwarteten Meßwerten E_k. Die damit gebildete Größe

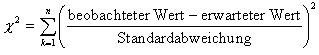
ist ein quantitatives Maß dafür, ob die beobachteten Meßwerte mit der angenommenen Verteilung beschrieben werden können.

Bei χ² = 0 wäre die Übereinstimmung vollkommen. Im allgemeinen sollten die einzelnen Terme der Summe etwa 1 sein, da im Mittel die Abweichung des Meßwertes vom Idealwert in der Größenordnung der Standardabweichung liegen sollte. Wenn die angenommene Verteilung die Messungen richtig beschreibt, sollte χ² ≅ n oder kleiner sein, da die Summe n Terme umfaßt. Ist dagegen χ ² viel größer als n, dann liegt die Vermutung nahe, daß die Meßwerte nicht der erwarteten Verteilung folgen.

4. Fehlerfortpflanzung

Funktionen mehrerer Variabler

Im allgemeinen Fall beruht die Bestimmung einer unbekannten Größe q auf der Messung mehrerer Variabler x, y, usw. Unter der Annahme, daß die Fehler der einzelnen Variablen unabhängig und normalverteilt sind, erhält man die Unsicherheit für q (Fehlerfortpflanzung) aus der Beziehung

.

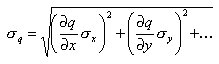
Kovarianz in der Fehlerfortpflanzung

Um festzustellen, ob die Fehler zweier Meßgrößen x und y tatsächlich unabhängig sind, bildet man die Kovarianz. Darunter versteht man einen Ausdruck der Form

.

Bei einer Abhängigkeit (z.B. zu großes x ergibt stets ein zu großes y) haben die Klammern stets das gleiche Vorzeichen, und die Varianz ist groß. Bei unabhängigen Meßwerten sollte man erwarten, daß sich die Kovarianz nach vielen Messung dem Wert null nähert.

Lineare Regression (Methode der kleinsten Quadrate)

Mit dieser Methode wird die Gerade y = A + Bx (d.h. die Konstanten A und B) bestimmt, die am besten den Zusammenhang zwischen zwei Variablen x und y wiedergibt, von denen angenommen wird, daß zwischen ihnen ein linearer Zusammenhang besteht (Methode der kleinsten Quadrate, lineare Regression).

Auch hier geht man wieder von der Wahrscheinlichkeit aus, die beobachteten Wertepaare (x, y) zu erhalten, und berechnet die Größen A und B, für die die Wahrscheinlichkeiten maximal sind.

Unter der Annahme, daß nur die y-Werte unsicher sind und diese Werte um den wahren Wert von y mit dem Breitenparameter σ_y normalverteilt sind, sind die Bestwerte für A und B gegeben durch

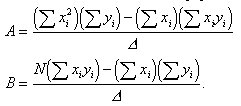
Die Abkürzung Δ bedeutet

.

Diese Beziehungen liefern die Bestwerte für A und B auf der Grundlage der gemessenen Punkte (x_i, y_i), ..., (x_N, y_N).

Wenn nach der Unsicherheit dieser Größen gefragt wird, muß erst etwas über die Unsicherheit der Meßwerte von y_i gesagt werden. Die y_i sind nicht Meßwerte derselben Größe, sondern sie sind mit den (als fehlerfrei angenommenen) x_i-Werten durch die Geradengleichung A + Bx_i verknüpft. Also sind die Abweichungen

normalverteilt und alle mit derselben Breite σ_y beim Wert 0 zentriert. Auch hier kann das Prinzip der größten Wahrscheinlichkeit angewendet werden. Es liefert als besten Schätzwert für σ_y das Resultat

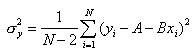
Es darf hier nicht durch die Anzahl der Wertepaare N dividiert werden, sondern durch die Anzahl der Freiheitsgrade. Da die Wertepaare bereits benutzt wurden, um die Konstanten A und B zu berechnen, sind nur noch N – 2 dieser Wertepaare voneinander unabhängig und dürfen für die Berechnung verwendet werden. Für die Unsicherheiten von A und B ergeben sich damit die Beziehungen:

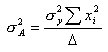
und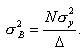

Nach der Methode der kleinsten Quadrate lassen sich Meßwertepaare auch an andere Beziehungen (z.B. Polynome, Exponentialfunktion usw.) anpassen.

Linearer Korrelationskoeffizient

Von der linearen Regression zu unterscheiden ist eine Fragestellung, bei der untersucht werden soll, ob zwischen zwei Meßgrößen ein z.B. linearer Zusammenhang (Korrelation) besteht. So könnte man z.B. daran interessiert sein, herauszufinden, ob Studenten, die in den Übungen hohe Punktzahlen, d.h. gute Ergebnisse erreichen, auch in der Abschlußprüfung gut abschneiden.

Dazu muß geprüft werden, wie gut eine Menge von Meßwertepaaren (x_i, y_i), ..., (x_N, y_N) einer linearen Beziehung gehorcht. Dazu muß der lineare Korrelationskoeffizient gebildet werden. Dieser ist definiert zu

.R kann zwischen +1 und -1 liegen. Positive Werte wären das erwartete Ergebnis, negative Werte dagegen würden bedeuten, daß gute Übungsergebnisse zu schlechten Abschlußprüfungen führen. Für diese Werte liegen die Punkte dicht bei einer Geraden. Für r = 0 besteht keine Korrelation zwischen den x- und y-Werten.

Literatur:

John R. Taylor: Fehleranalyse, VCH Verlagsgesellschaft, Weinheim 1988;
G.L. Squires: Meßergebnisse und ihre Auswertung, de Gruyter, Berlin, 1971.

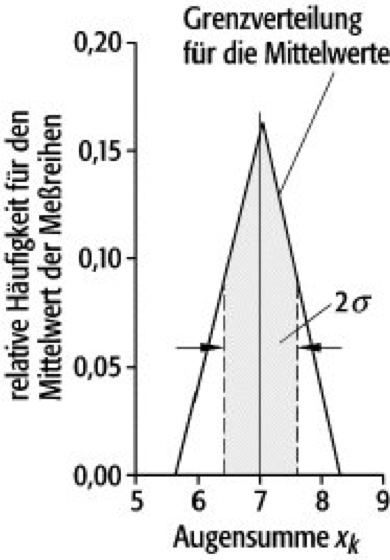
Fehlerrechnung 1: Die obere Teilabbildung zeigt in Form eines Stabdiagramms die relative Häufigkeit, mit der beim 20maligen Werfen von zwei Würfeln eine bestimmte Augensumme erzielt wurde. Die für dieses Experiment leicht zu berechnenden Wahrscheinlichkeiten (= Ergebnis bei unendlich vielen Würfen = Grenzverteilung) sind ebenfalls eingetragen. Unten sieht man die Grenzverteilung für die Mittelwerte, die aus jeder Meßreihe errechnet werden können. Sie ist, wie erwartet, bedeutend schmaler: Die Mittelwerte streuen weniger als die Einzelmessungen (Abszissenwerte beachten!).

Fehlerrechnung 2: So ändert sich die Verteilung der Meßwerte in einem realen physikalischen Meßprozeß, wenn man die Anzahl der Messungen erhöht. Die Verteilung wird glatter, ist symmetrisch und hat die Form einer Glockenkurve. Dies ist die gesuchte Grenzverteilung für das Experiment.

Fehlerrechnung 3: Drei Beispiele für Experimente, die mit Hilfe der Binomialverteilung mathematisch korrekt beschrieben werden können. Auch hier wird mit steigendem Mittelwert für die Verteilung eine symmetrische Glockenkurve beobachtet.

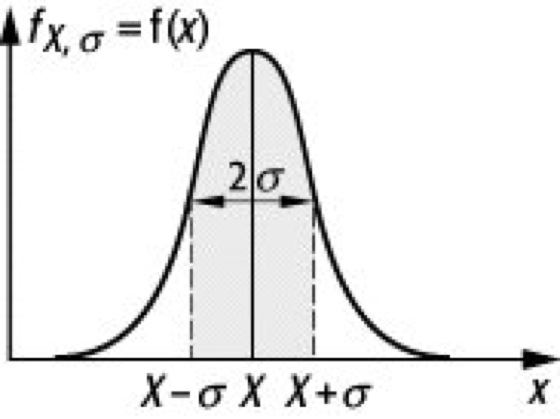
Fehlerrechnung 4: Es kann mathematisch exakt gezeigt werden, daß sowohl die Binomial- als auch die Poisson-Verteilung für große Mittelwerte in die sogenannte Gauß- oder Normalverteilung übergeht. Sie ist charakterisiert durch den Wert X und die Breite 2σ. Diese beiden Größen entsprechen den Begriffen Bestwert und Unsicherheit der Messung.

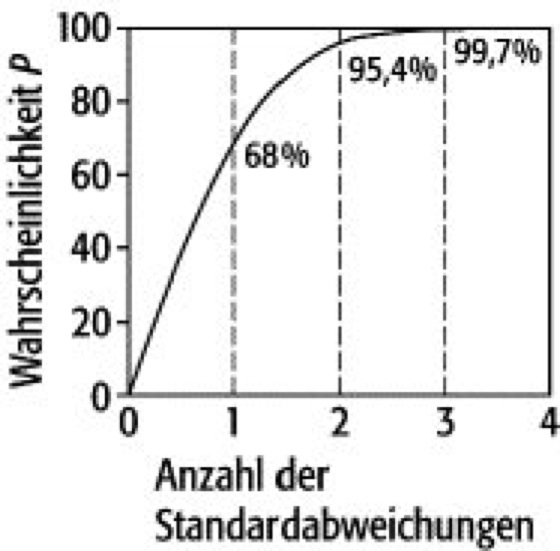
Fehlerrechnung 5: Wahrscheinlichkeit, mit der der Mittelwert einer neuen Meßreihe innerhalb der Fehlergrenzen liegt, wenn als Fehlergrenze mehr als eine Standardabweichung angegeben wird. Man erkennt, daß eine Verdreifachung des Fehlerbereichs bereits eine fast hundertprozentige Sicherheit bedeutet, mit einem neuen Ergebnis innerhalb dieser Grenzen zu liegen.