Psychologie: Das Geheimnis der Rorschach-Formen
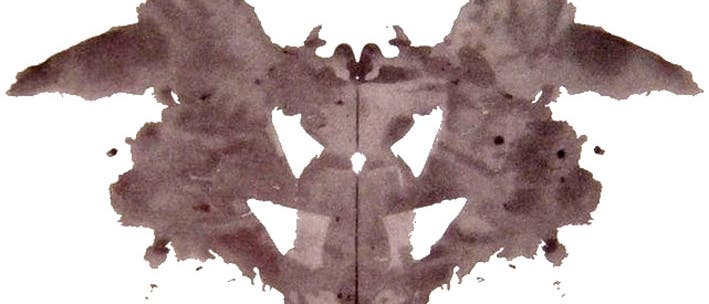
Ein Team amerikanisch-australischer Forscher glaubt, das Geheimnis hinter den berühmten Rorschach-Bildern gelüftet zu haben. Mit einem Satz bestehend aus zehn dieser Farbklekse versuchte der Schweizer Psychoanalytiker Hermann Rorschach im Jahr 1921, die seelische Gesundheit seiner Patienten zu ergründen. Ein auf den Faltbildern basierender Test entwickelte sich im 20. Jahrhundert zu einem weltbekannten Diagnoseverfahren, dessen Aussagekraft aus heutiger Sicht allerdings umstritten ist.
Menschen fühlen sich von den Tintenbildern an etliche verschiedene Objekte erinnert. Bei einigen der Formen sind bis zu 300 verschiedene Deutungen bekannt. Nun meint eine Gruppe aus Physikern und Psychologen um Richard P. Taylor von der University of Oregon in Eugene den Grund dafür gefunden zu haben, weshalb manche Klekse ein größeres Assoziationspotenzial bergen als andere: Offenbar ist die Deutung der Formen immer dann besonders ergiebig, wenn ihr Rand einen vergleichsweise geringen Grad an Komplexität aufweist.
Die Struktur der Tintenklekse lässt sich mit so genannten Fraktalen beschreiben. Darunter verstehen Mathematiker unregelmäßige Formen, die sich wiederholen, wenn man den Rand eines Objekts vergrößert. Sie kommen auch in der Natur vor, zum Beispiel bei Schneeflocken, Wolken und Blumenkohlköpfen. Bereits 1990 stellten Wissenschaftler die Vermutung auf, dass Wolken und andere Naturformen vor allem dann die Fantasie von Betrachtern anregen, wenn diese nur schwache fraktale Merkmale aufweisen.
Das gelte auch für Rorschach-Bilder, schreibt nun das Team um Taylor. Die Forscher entwickelten eine Kennzahl, die Werte zwischen 1,0 und 2,0 annehmen kann und die als Maß für die fraktale Komplexität am Rand der zehn historischen Rorschach-Figuren diente. Liegt die Zahl bei 1,0, ist der Rand einer Form glatt wie eine Linie. Beträgt sie annähernd 2,0, ist die Umrandung einer Figur von Fraktalen zerklüftet.
Anschließend verglichen die Forscher diese Kennzahlen mit Aufzeichnungen aus den 1930er und 1950er Jahren, in denen festgehalten wurde, wie viele unterschiedliche Objekte die befragten Patienten mit jeder der zehn Rorschach-Figuren assoziierten. Dabei stießen sie auf eine deutliche Korrelation: Farbklekse mit niedriger Kennzahl hatten bei Rorschach-Tests die meisten verschiedenen Deutungen hervorgerufen. Und je näher die Zahl dem Wert 2,0 kam, desto weniger Assoziationen hatten die Testabsolventen.
Dieser Trend zeigte sich ebenfalls bei einem Test in der Gegenwart: Die Wissenschaftler ließen einen Computeralgorithmus Rorschach-Formen mit verschiedenen fraktalen Komplexitäten erstellen und zeigten diese anschließend 23 amerikanischen Psychologiestudenten. Auch diese erkannten umso mehr verschiedene Objekte in einer Rorschach-Form, je glatter deren Oberfläche war.

Schreiben Sie uns!
Beitrag schreiben