Lexikon der Physik: Standardmodell der Kosmologie
Standardmodell der Kosmologie, das aus der Anwendung der Allgemeinen Relativitätstheorie auf die Kosmologie sowie aus astronomischen und teilchenphysikalischen Messungen gebildete Modell, welches die Entstehung und Entwicklung des Weltalls beschreibt. Seine Grundlage bildet die Vorstellung eines isotropen und homogenen Universums (kosmologisches Prinzip). Man mag sie als erste Näherung für das heutige Universum auffassen, und für die Frühphase des Universums trifft sie sogar exakt zu. Aus dem kosmologischen Prinzip folgt aber nun, daß es Koordinaten gibt, in denen die Metrik die Form
annimmt. Dabei ist ![]()
der sog. Weltradius oder Skalenfaktor; er ist ein Maß für die Ausdehnung des Universums. ![]()
, ![]()
und ![]()
sind räumliche Koordinaten, ![]()
ist die zeitliche Koordinate und ![]()
ist ein Parameter, welcher die Werte 0, -1 und +1 annehmen kann. Man erhält also drei verschiedene Lösungstypen. Diese Metrik wird auch als Friedmann-Robertson-Walker-Metrik bezeichnet.
Unabhängig vom Wert des Parameters ![]()
ist die durch die Friedmann-Robertson-Walker-Metrik beschriebene Raumzeit gekrümmt (das folgt bereits aus der Tatsache, daß das Universum nicht leer, sonder materieerfüllt ist). Die dreidimensionalen Unterräume ![]()
können hingegen flach ( ![]()
), ähnlich einer Kugelfläche positiv gekrümmt ( ![]()
) oder ähnlich einer Sattelfläche negativ gekrümmt ( ![]()
) sein. Berechnet man das Volumen ![]()
dieser Unterräume, so ergibt sich, daß dieses für ![]()
und ![]()
unendlich ist, während es für ![]()
endlich und durch ![]()
gegeben ist. Für ![]()
liegt also ein geschlossenes Universum vor.
Die Annahme eines statischen Universums widerlegte E. Hubble durch die Entdeckung der Rotverschiebung und damit eines expandierenden Universums; für relativ nahe Galaxien ist die Rotverschiebung proportional zur ihrer Entfernung (Hubble-Fluß). Die Hubble-Konstante![]()
gibt die momentane (t = t0) Expansion des Universums an.
Die zeitliche Entwicklung des Weltradius erhält man, wenn man die Robertson-Walker-Lösung in die Einstein-Gleichungen einsetzt und annimmt, daß der Materiegehalt des Universums durch eine perfekte Flüssigkeit beschrieben werden kann, wobei wegen des kosmologischen Prinzips Dichte und Druck nur von der Zeit, nicht aber vom Ort abhängen können, ![]()
. Als Zustandsgleichung betrachtet man zumeist die beiden Grenzfälle ![]()
und ![]()
. Die erste der beiden Gleichungen beschreibt inkohärente Materie; sie setzt nichtrelativistische Teilchen voraus und ist eine brauchbare Näherung für unser heutiges Universum. Die zweite Gleichung gilt exakt für elektromagnetische Strahlung und näherungsweise für relativistische Teilchen. Sie ist für das frühe Universum angemessen. Für eine gemeinsame Diskussion beider Fälle setzt man ![]()
, wobei der erste Summand die materiedominierte Materiedichte und der zweite Summand die strahlungsdominierte Materiedichte ist. Dann folgt aus den Einsteinschen Feldgleichungen:
wobei
ist. ![]()
ist hierin eine Abkürzung für ![]()
, ![]()
eine Abkürzung für ![]()
. Beides sind Konstanten (folgt aus den Feldgleichungen). Da ![]()
und ![]()
beide positiv sind, verhalten sich die Terme ![]()
und ![]()
im effektiven Potential ![]()
ähnlich, und es ergibt sich die in Abb. 1 gezeigte qualitative Skizze für den Weltradius ![]()
.
Man sieht, daß sich für ![]()
und ![]()
ein offenes Universum ergibt, welches ewig expandiert, während sich für ![]()
ein geschlossenes Universum ergibt, welches nach Erreichen einer maximalen Ausdehnung wieder kontrahiert (und dann vermutlich neu ›explodiert‹, so daß eine Sequenz von Zyklen vorliegt). Welche der drei möglichen Lösungen vorliegt, hängt von der heutigen Materiedichte ![]()
ab. Für ![]()
wird ![]()
negativ, für ![]()
positiv und für ![]()
gleich Null, wobei ![]()
die kritische Materiedichte![]()
ist. Um zu entscheiden, ob das Universum geschlossen ist oder nicht, muß man also die Hubble-Konstante und die heutige Materiedichte durch astronomische Beobachtungen bestimmen. Ersteres geschieht durch Ermittlung der Relation zwischen Rotverschiebung und Entfernung von Galaxien, letzteres durch Galaxienzählungen. Führt man derartige Messungen durch, so erhält man für ![]()
einen Wert, der größenordnungsmäßig etwa 1 / 10 des kritischen Wertes beträgt. ![]()
scheint also negativ und damit unser Universum offen zu sein. Aber es könnte neben der sichtbaren auch noch dunkle Materie geben, die einen erheblichen Anteil an der Gesamtmaterie im Universum besitzen und ![]()
in die Nähe der kritischen Dichte oder gar darüber hinaus bringen könnte (für eine genauere Diskussion siehe Kosmologie).
Wenn man davon ausgeht, daß die Strahlungsära nur einen sehr kleinen Anteil am Gesamtalter ![]()
ausmacht und ![]()
einfachheitshalber gleich Null wählt, so ergibt sich für das theoretische Alter des Universums
wenn man für die Hubble-Konstante den Wert 50 km / s / Mpc zugrundelegt. Das ist verträglich mit astronomischen Beobachtungen, welche für das Alter der Milchstraße eine untere Schranke von 1010 Jahren angeben.
Da das Standardmodell der Kosmologie zu ![]()
für ![]()
führt, muß es in der Vergangenheit einen singulären Zustand gegeben haben, der auch als Urknall (Big Bang) bezeichnet wird. Welche Phasen durchlief nun das Universum nach dem Urknall? Je kleiner der Weltradius ![]()
war, umso höher war die Temperatur. Da hier die Frühphase des Universums betrachtet wird, ist die Materie strahlungsdominiert. Verwendet man also ![]()
und drückt sie durch das Stefan-Boltzmann-Gesetz aus, so erhält man den gesuchten Zusammenhang: ![]()
Die (Strahlungs-)Temperatur ist also umgekehrt proportional zum Weltradius. Es ergeben sich folgende rückwärts in der Zeit angeordnete und durch die Höhe der Temperatur charakterisierte Phasen:
Phase 1: Für T< 3000 K ist die Materie weitgehend nicht-ionisiert (sobald T unter TR ≈ 3000 K sinkt (das entspricht einem Weltalter von etwa 400 000 Jahren), findet die Rekombination statt) und somit von der Strahlung entkoppelt. Dadurch liegen zwei Temperaturen im Universum vor: Die Strahlungstemperatur, die weiterhin umgekehrt proportional zum Weltradius ist, sowie die Materietemperatur Tm. Man kann zeigen, daß letztere umgekehrt proportional zum Quadrat des Weltradius ist, mit zunehmender Expansion also stärker abnimmt als die Strahlungstemperatur.
Phase 2: Für T > 3000 K ist die Materie hinreichend ionisiert, so daß sich ein Gleichgewicht mit der Strahlung einstellt. Je weiter man in der Zeit zurück geht, desto mehr stellt sich ein Zustand ein, in welchem ein vollständig ionisiertes Plasma im Gleichgewicht mit dem Photonengas vorliegt.
Phase 3: Für kBT ≈ 10 ... 100 keV (t ≈ 100 ... 104 s) finden Kernreaktionen statt. Es kommt zur Bildung von Atomkernen leichter Elemente.
Phase 4: Für kBT ≈ 1 MeV (t ≈ 2 s) findet e+e--Paarbildung statt. Steigt die Temperatur weiter, so setzt Teilchen-Antiteilchen-Produktion auch für andere Teilchensorten ein.
Phase 5: Für ![]()
kommt man zunächst in den Bereich, wo die sog. Grand Unified Theories (GUT) Anwendung finden. Diese sind allerdings experimentell noch nicht gut verifiziert. Geht man noch näher an den Urknall heran, so kommt man in den Bereich des Planck-Regimes, in dem Quanteneffekte der Gravitation wichtig werden und eine noch zu findende Quantengravitation ihre Anwendung finden könnte. Diese könnte helfen, die in der klassischen Allgemeinen Relativitätstheorie unvermeidliche Singularität ![]()
zu beheben.
Die abgekoppelte Strahlung ist noch heute als kosmischeHintergrundstrahlung beobachtbar. Sie ist außerordentlich isotrop, was bedeutet, daß zum Zeitpunkt der Rekombination das Universum extrem homogen und isotrop gewesen sein muß – eine nachträgliche Bestätigung des kosmologischen Prinzips.
Die weitere Entwicklung des Universums:
In der Phase 3 fanden Kernreaktionen statt, die zur Bildung leichterer Elemente führten. Später, als sich Sterne bildeten, entstanden auch in ihnen durch Kernfusionen weitere Elemente, sowohl leichtere als auch schwerere.
Die Isotropie der Hintergrundstrahlung zeigt, daß bis zur Rekombination das Universum praktisch homogen gewesen ist. Die Strukturen können also erst später entstanden sein. Man nimmt an, daß diese aus anfänglich infinitesimalen Dichtefluktuationen entstanden sind. Diese mögen sich spontan als statistische Schwankungen gebildet haben. Vielleicht wurde ihre Genese aber auch durch physikalische Prozesse bewirkt. Weiter ist zu untersuchen, ob einmal vorhandene Dichtefluktuationen instabil oder stabil sind, d.h. anwachsen und sich schließlich zu Strukturen ausdifferenzieren oder wieder verschwinden bzw. sich als Schallwellen fortpflanzen. Ist die Gravitationskraft mächtig genug, sie zu verstärken, oder führt die Expansion des Universums dazu, daß sie wieder abgebaut werden? Und welche Rolle spielt der Druck? Ein eventuelles Anwachsen muß nach dem oben Gesagten dann nach der Rekombination stattgefunden haben. (Weitere Details zu Fragen der Entwicklung des Universums: Kosmologie).

Standardmodell der Kosmologie 1: Zeitliche Entwicklung des Weltradius. Für ![]()
und ![]()
expandiert das Universum ewig; für ![]()
hingegen ergibt sich ein pulsierendes Weltmodell.
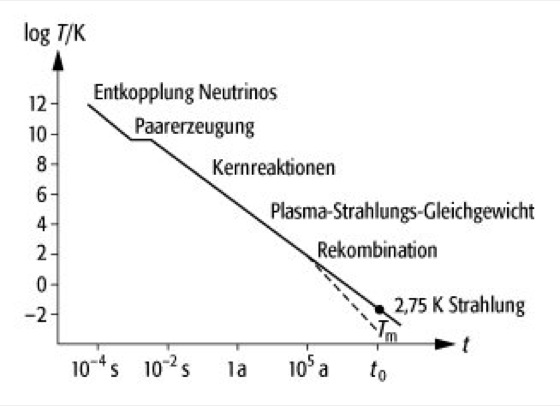
Standardmodell der Kosmologie 2: Die verschiedenen Phasen des Universums. In dieser doppelt-logarithmischen Darstellung sind die einzelnen Prozesse, die während der Expansion und mit zunehmender Abkühlung stattfanden, dargestellt. Das Plateau bei T = 1010 K entsteht dadurch, daß bei der Paarerzeugung neue Freiheitsgrade entstehen, welche Energie absorbieren. Bei T ≈ 104 K entkoppeln Strahlung und Materie, das Universum wird ›durchsichtig‹. Von nun an gibt es zwei Temperaturen im Universum: Die Strahlungstemperatur, welche heute (Weltalter = t0) 2,75 K beträgt, und die durchschnittliche Temperatur der Materie Tm, welche geringer ist, da sie umgekehrt proportional zum Weltradius ist.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.