Der Mathematische Monatskalender: Leonhard Euler (1707–1783): Der produktivste Mathematiker aller Zeiten
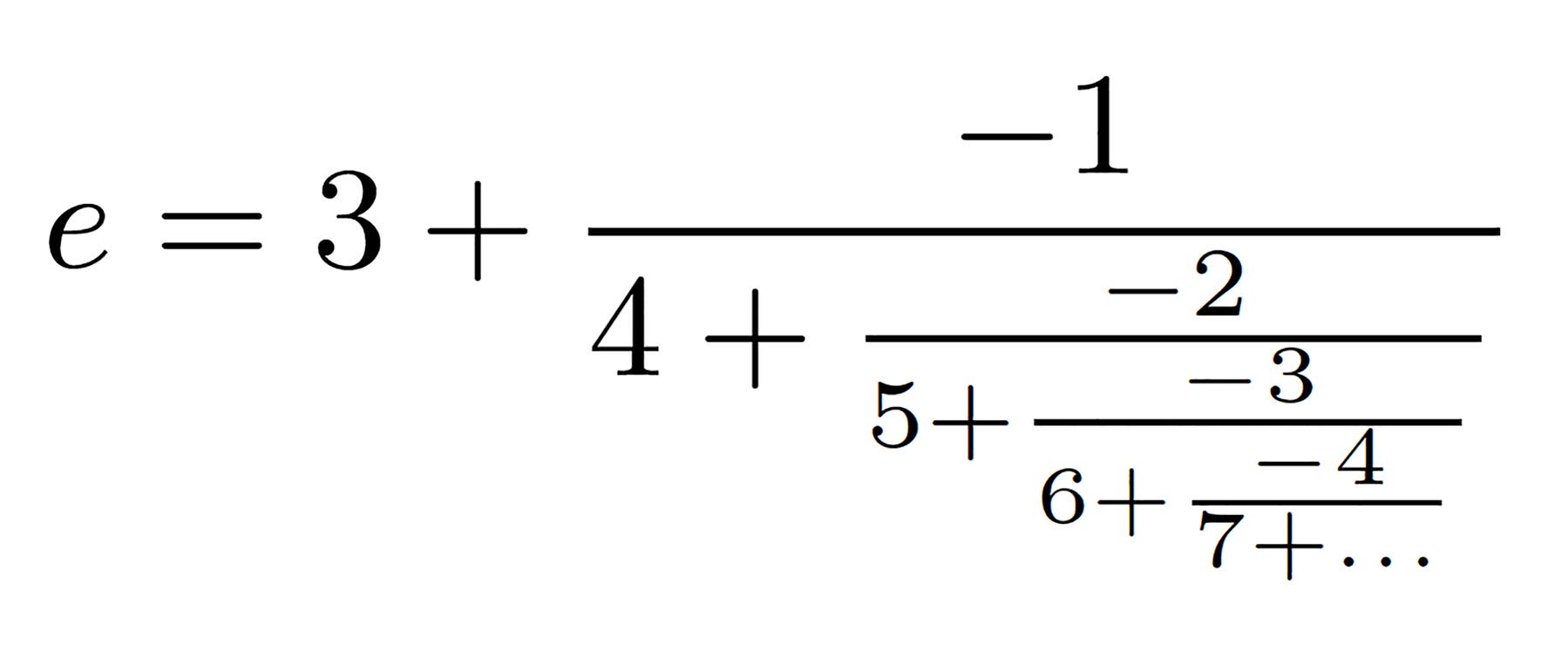
Leonhard Euler war zweifelsohne der produktivste Mathematiker aller Zeiten; er verfasste Bücher und umfangreiche Arbeiten zu vielen Teilbereichen der reinen und angewandten Mathematik, der Physik, zur Astronomie, Geodäsie, Kartographie, Musik und zum Schiffsbau - in lateinischer, französischer und deutscher Sprache.
Er schrieb nicht nur viel, sondern brachte bei allen Themen, mit denen er sich beschäftigte, mit unglaublicher Kreativität neuartige Ideen ein und eröffnete durch seine Beiträge sogar neue Teilbereiche der Mathematik. Auf der aktuellen Schweizer Briefmarke ist neben dem Dürerschen Polyeder und der Polyederformel ein Portrait Eulers aus dem Jahr 1753 abgedruckt, auf dem erkennbar ist, dass er schon früh mit einem Augenleiden zu kämpfen hatte.
Euler wird in Basel als Sohn eines Pfarrers geboren; auch seine Mutter stammt aus einer Pfarrersfamilie. Da die Schule, die er besucht, den Jungen nicht angemessen fördern kann, unterrichtet ihn sein Vater selbst. Mit 14 Jahren besucht Euler philosophische Vorlesungen an der Universität und schließt das Studium mit einem Vergleich der Ideen von Descartes und Newton ab; mit 16 Jahren nimmt er, dem Wunsch seines Vaters entsprechend, ein Theologiestudium auf, wechselt dann aber zur Mathematik, nachdem Johann Bernoulli, ein Freund des Vaters, diesen davon überzeugt hat, dass Leonhard eine außergewöhnliche mathematische Begabung besitzt.
Mit 19 Jahren gewinnt er den zweiten Preis in einem Wettbewerb der Französischen Akademie der Wissenschaften mit einem Beitrag zur Frage, wie man Maste auf Segelschiffen optimal positioniert - man kann davon ausgehen, dass Euler bis dahin noch keine Ozeanschiffe gesehen hatte! Diesen angesehenen, jährlich ausgeschriebenen wissenschaftlichen Wettbewerb gewinnt er später insgesamt zwölfmal.
Vergeblich bemüht sich Euler um eine frei gewordene Physikprofessur in Basel, folgt dann 1727 Daniel und Jakob Bernoulli nach St.Petersburg an die drei Jahre zuvor von Peter dem Großen gegründete Russische Akademie der Wissenschaften. Hier soll er an der medizinischen Fakultät Vorlesungen über Anatomie und Physiologie halten, übernimmt jedoch bald (1730) eine Professur für Physik, 1733 für Mathematik (als Nachfolger von Daniel Bernoulli). 1734 heiratet er Katharina Gsell, Tochter eines aus der Schweiz stammenden Malers der Petersburger Akademie; in der glücklichen Ehe werden 13 Kinder geboren, von denen allerdings nur fünf die Kindheit überleben.
Innenpolitische Probleme in Russland veranlassen ihn 1741, von St. Petersburg als Direktor der mathematischen Klasse der Preußischen Akademie der Wissenschaften nach Berlin zu wechseln. Erster Präsident der Akademie wird Pierre Louis Moreau de Maupertuis (1698–1759), den er in seiner Arbeit intensiv unterstützt.
In den 25 Jahren in Berlin verfasst er nicht nur 380 wissenschaftliche Arbeiten, sondern kümmert sich auch um das Observatorium ebenso wie um die Botanischen Gärten und die Wasserversorgung der Gärten des Schlosses Sanssouci, der Sommerresidenz König Friedrichs des Großen in Potsdam. Mit seinen »Lettres à une princesse d’Allemagne sur quelques sujets de Physique et Philosophie« (Briefe an eine deutsche Prinzessin über verschiedene Gegenstände aus der Physik und Philosophie) schreibt er Texte für die Allgemeinheit, ähnlich auch seine »Vollständige Anleitung zur Algebra« (1770), deren Texte er einem Schneider zur Kontrolle der Verständlichkeit vorlegt. Durch die von ihm entwickelten Methoden zur Lösung von Differentialgleichungen (Gleichungen, in denen die Funktion und deren Ableitungen auftreten) gibt er der Physik neue Impulse.
Über 25 Jahre hinweg hält er Kontakte nach St. Petersburg aufrecht, korrespondiert intensiv mit seinem Freund Christian Goldbach (1690–1764), dem er viele, aber nicht alle Fragen beantworten kann: »Jede gerade Zahl größer als zwei kann als Summe zweier Primzahlen geschrieben werden.« (1742, Goldbach-Vermutung – bis heute nicht bewiesen)
1766 kehrt er wieder nach St. Petersburg zurück; in Berlin übernimmt Joseph-Louis Lagrange (1736-1813) seine Stelle. Trotz seiner bald eintretenden vollständigen Erblindung verfasst er dort noch über 400 weitere Werke, die er seinem Sohn und seinem Schwiegersohn diktiert. Als er 1783 stirbt, hat er insgesamt 866 Schriften verfasst (einsehbar unter http://math.dartmouth.edu/~euler/ ). Pierre Simon Laplace (1749-1827) kommentiert diese Werkfülle mit den Worten: »Lest Euler, lest Euler, er ist unser aller Meister.«
Mit seinen Lehrbüchern zur Analysis des Unendlichen (Introductio in analysin infinitorum), zur Differentialrechnung (Institutiones calculi differentialis) und Integralrechnung (Institutiones caluli integralis) trägt Euler wesentlich zur Systematisierung der Analysis bei. Zahlreiche Begriffe und Schreibweisen der Mathematik werden von ihm eingeführt, wie z. B. der Begriff der Funktion, die heute übliche Bezeichnung der trigonometrischen Funktionen, die Schreibweise \(f(x)\), das Summenzeichen \(\sum\) und »i« für die imaginäre Einheit der Komplexen Zahlen.
Von Euler stammt auch die Bezeichnung »e« für die Basis des natürlichen Logarithmus. Die Zahl wird heute als Eulersche Zahl bezeichnet, obwohl sie lange vor Euler von John Napier (1550-1617) entdeckt worden war.
1734 verblüfft Euler die Fachwelt mit einer sensationellen Entdeckung: Dass die harmonische Reihe \( \left( 1+ \frac{1}{2} + \frac{1}{3}+...+ \frac{1}{n}\right) _{n\in \mathbb{N}}\) divergiert, war bereits auf verschiedene Arten bewiesen worden; man vermutete, dass die entsprechende unendliche Reihe der reziproken Quadratzahlen konvergierte; Johann Bernoulli konnte für die Reihe \(\left( 1+ \frac{1}{2^2} + \frac{1}{3^2}+...+ \frac{1}{n^2}\right) _{n\in \mathbb{N}}\) sogar eine konvergente Majorante angeben, die den Grenzwert zwei hat; er scheiterte jedoch bei der Bestimmung eines Grenzwerts ebenso wie vor ihm Leibniz, Stirling, de Moivre und andere.
Euler geht mit den Potenzreihenentwicklungen von Funktionen virtuos um: Die Sinusfunktion lässt sich als Potenzreihe schreiben: \(\sin(x)= x – \frac {x^3}{3!} + \frac{x^5}{5!}-\frac {x^7}{7!}+...;\) hieraus erhält er die Darstellung \( f(x)=\frac{sin(x)}{x} = 1 – \frac{x^2}{3!}\) \(+ \frac{x^4}{5!} – \frac {x^6}{7!}+..\)
Diese Funktion hat an der Stelle \(x=0)\) den Wert 1 und die Nullstellen liegen bei \(±\pi\), \(± 2\pi\), \(± 3\pi\)...der Funktionsterm lässt sich also als unendliches Produkt von Linearfaktoren schreiben. Multipliziert man nun das unendliche Produkt von Linearfaktoren aus und vergleicht die auftretenden Koeffizienten von \( x^2\), dann folgt: \(\frac{1}{3!} = \frac{1}{6} = \frac{1}{\pi^2} + \frac{1}{4 \pi^2} + \frac{1}{9\pi^2} +...\), also \( 1+ \frac{1}{4} +\frac{1}{9} +\frac{1}{16}+ ..=\frac{\pi^2}{6} = 1,6449340668..\)
Betrachtet man nur die geraden Potenzen dieser unendlichen Summe, so erkennt man: \(1+ \frac{1}{4} +\frac{1}{16} +\frac{1}{36} +\frac{1}{64}+..=\) \( \frac{1}{4} \cdot \) \( (1+ \frac{1}{4} +\frac{1}{9} +\frac{1}{16}+..) \) \(= \frac{\pi^2}{24} 0 0,4112335167\)
Für die ungeraden Potenzen ergibt sich:
\(1+ \frac{1}{9} + \frac{1}{25}+\frac{1}{49}+\) \(..= \frac{\pi^2}{6} – \) \( \frac{ \pi^2}{24} \frac {\pi^2}{8} = 1,233700550\)
Außerdem erhält man:
\( f( \frac{\pi}{2}) = \frac{1}{\pi /2}) = (1-\frac{1}{4}) (1-\frac{1}{16}) (1-\frac{1}{26})\) \( \cdot..=\frac{3}{4} \cdot \frac{15}{16} \cdot \frac{35}{36}\) \( \cdot.. = \frac{3\cdot3 \cdot5 \cdot5 \cdot 7\cdot7 \cdot..}{2\cdot 2\cdot4 \cdot4 \cdot6 \cdot6\cdot..}\)
ein Ergebnis, das John Wallis (1616-1703) im Jahr 1650 auf völlig andere Weise hergeleitet hatte. (Übrigens: Im 17. Jahrhundert war es noch üblich, mit unendlichen Folgen und deren Grenzwerten intuitiv zu rechnen, ohne exakte Konvergenzbeweise zu führen.)
Mit dem gleichen Ansatz des Koeffizientenvergleichs leitet Euler her, dass die Summe der reziproken vierten Potenzen der natürlichen Zahlen gegen \(\frac{\pi^4}{90}\) konvergiert, die der 6. Potenzen gegen \(\frac{\pi^6}{90}\) usw. Er setzt seine Herleitungen bis zur 26. Potenz fort ... (Bis heute ist übrigens noch keine Methode gefunden worden, die Grenzwerte für ungerade reziproke Potenzen exakt zu bestimmen.)
Euler verallgemeinert das Problem der unendlichen Summen von reziproken Potenzen, indem er für beliebige Exponenten die Zeta-Funktion einführt: \(\zeta(s) = 1+ \frac{1}{2^s} + \frac{1}{3^s} + \frac{1}{4^s} + ...\) und eine erstaunliche Produktdarstellung hierfür herleitet: \(\zeta(s) = \frac{1}{1-\frac{1}{2^s}} \cdot \frac{1}{1-\frac{1}{3^s}} \cdot \frac{1}{1-\frac{1}{5^s}} \cdot ...,\) in deren Term nur Primzahlpotenzen auftreten.
Er entdeckt, dass die Folge der Summe der Stammbrüche (Harmonische Reihe) zwar divergiert, dies jedoch besonders langsam geschieht, und dass man diese Reihe mit den Werten der natürlichen Logarithmusfunktion vergleichen kann. Die Folge \(c_n = 1+ \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + ..\) ist konvergent gegen eine Zahl \(\gamma = 0,577215664....\)
Euler berechnet 1781 diesen Grenzwert auf 16 Stellen genau; Lorenzo Mascheroni (1750–1800) auf 32 Stellen (so genannte Euler-Mascheroni-Konstante).
Zeitgleich zu Jean d'Alembert (1717–1783) entwickelt er das formale Rechnen mit komplexen Zahlen und untersucht Funktionen mit komplexen Variablen; komplexe Zahlen haben jedoch für ihn keine reale Bedeutung.
1743 entdeckt er bei der Betrachtung der Potenzreihen für komplexe Argumente den einfachen Zusammenhang zwischen trigonometrischen Funktionen und Exponentialfunktion (Eulersche Formel):
\[ \cos(z) + i \cdot \sin(z) = \left( 1- \frac{z^2}{2!} + \frac{z^4}{4!} \mp ...\right) + i \cdot \left( \frac{z}{1!} – \frac{z^3}{3!} + \frac{z^5}{5!} \mp ... \right) \] \[ 1 + \frac{iz}{1!} + \frac{(iz)^2}{2!} + \frac{(iz)^3}{3!} + ... = e^{iz} \]
Für \(z=\pi\) erhält man die bemerkenswerte Beziehung: \(e^{i\pi} + 1 =0\), für \(z=\pi/2\): \(i= e^{\frac{i\pi}{2}} \), woraus unter anderem \(i^i = (e^{\frac{i\pi}{2}})^i = e^{-\frac{\pi}{2}}\) folgt.
Da \(\int_0^\infty x^0 e^{-x}\ dx =\) \(\int_0^\infty x^1 e^{-x}\ dx =1,\) \( \int_0^\infty x^2 e^{-x}\ dx =2,\) \(\int_0^\infty x^3 e^{-x}\ dx =6, ...\) gilt, hat Euler die Idee, mithilfe von \(\Gamma (z) = \int_0^\infty x^{z-1} e^{-x}\ dx\) die Fakultäten zu interpolieren und die Definition auf beliebige \(z \in \mathbb{R} \) zu erweitern; allgemein gilt nämlich: \(\Gamma(z+1) = z \cdot \Gamma(z) \) und \(\Gamma(1)=1\), also für \(n \in \mathbb{N} \): \(\Gamma(n+1)=n!\) (so genannte Gammafunktion).
In der Zahlentheorie liefert Euler gleich drei verschiedene Beweise für den so genannten Kleinen Fermatschen Satz, der 1634 von Pierre de Fermat (1601–1665) formuliert, aber nicht bewiesen wurde: » Ist \(p\) eine Primzahl und \(a\) eine ganze Zahl, die nicht durch \(p\) teilbar ist, dann ist \(p\) ein Teiler von \(a^{p-1} – 1.\)«
Die Vermutung Fermats, dass alle Zahlen der Form \(2^{2^n} + 1\) Primzahlen sind, widerlegt er durch Faktorisierung von \(2^{32}+1 = 4294967297 = 641 \cdot 6700417,\) wobei er bei der Suche nach geeigneten Faktoren den Kleinen Fermatschen Satz und einen Satz über die eindeutige Darstellbarkeit von Zahlen des Typs \(4k+1\) verwendete: »Alle Primahlen, die bei der Division durch 4 den Rest 1 lassen, lassen sich eindeutig (das heißt nur auf eine Weise) als Summe zweier Quadratzahlen schreiben (und umgekehrt).« Auch dieser Satz war von Fermat gefunden worden, erst Euler gelingt der Beweis. Die Fermatsche Vermutung, dass die Gleichung \(x^n+y^n=z^n\) für \(n > 2\) keine Lösungen in der Menge der ganzen Zahlen hat, beweist Euler für den Fall \(n = 3.\)
Im Zusammenhang mit seinem dritten Beweis des Kleinen Fermatschen Satzes definiert er 1763 die Funktion \(\varphi(n)\), die ihm zu Ehren als Eulersche Funktion bezeichnet wird. Diese ordnet jeder natürlichen Zahl die Anzahl der zu \(n\) teilerfremden natürlichen Zahlen \(k\) mit \(k \leq n\) zu; zum Beispiel gilt \(\varphi(a \cdot b) = \varphi(a) \cdot \varphi(b), \) falls \(a\) und \(b\) zueinander teilerfremd sind. Bemerkenswert ist, dass sich diese Funktion in Produktform mithilfe der reziproken Primteiler von \(n\) schreiben lässt, das Produkt aber stets ganzzahlig ist:
\[ \varphi(n) = n \cdot \left( 1- \frac{1}{p_1} \right) \cdot \left( 1- \frac{1}{p_2} \right) \cdot \left( 1- \frac{1}{p_3} \right) \cdot ... \cdot \left( 1- \frac{1}{p_r} \right) \]
Beispiel: 10 ist teilerfremd zu 1, 3, 7, 9 und es gilt: \( \varphi(10) = 10 \cdot \left( 1- \frac{1}{2} \right) \cdot \left( 1- \frac{1}{5} \right) \) \(= 10 \cdot \frac{1}{2}\cdot{4}{5} = 4\)
Griechische und arabische Mathematiker waren fasziniert von den sogenannten befreundeten Zahlen 220 und 284, für die gilt, dass die Summe der echten Teiler jeweils die Partnerzahl ergibt: 220 = 1 + 2 + 4 + 71 + 142 und 284 = 1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 +55 + 110
Erst um 1300 entdeckt der arabische Mathematiker Ibn al Banna (1256–1321), dass auch die Zahlen 17 296 und 18 416 diese bemerkswerte Eigenschaft besitzen; Descartes findet 1638 noch ein weiteres Paar: 9 363 584 und 9 437 056. Zwischen 1747 und 1750 entdeckt Euler weitere 58 Zahlenpaare mit dieser Eigenschaft, weil es ihm gelingt, deren Bildungsprinzip zu durchschauen und eine Berechnungsvorschrift anzugeben (es gibt – wie man heute weiß – noch weitere befreundete Zahlen, die man auf diese Weise nicht berechnen kann).
Euler leitet eine Methode her, wie man die Anzahl der möglichen Zerlegungen einer natürlichen Zahl in lauter verschiedene Summanden berechnen kann, und beweist, dass diese Anzahl genauso groß ist wie die Anzahl der Zerlegungen einer natürlichen Zahl in lauter (nicht notwendig verschiedene) ungerade Summanden. Auch diesen Beweis führt er wieder unter Verwendung von unendlichen Summen und Produkten. Beispiel: Die Zahl 7 lässt sich auf jeweils vier Arten zerlegen: 7 = 1 + 6 = 2 + 5 = 3 + 4 = 1 + 2 + 4 und 7 = 5 + 1 + 1 = 3 + 3 + 1 = 3 + 1 + 1 + 1 + 1 = 1 + 1 + 1 + 1 + 1 + 1+1
Euler beschäftigt sich auch intensiv mit geometrischen Problemen; er entdeckt beispielsweise, dass in jedem beliebigen Dreieck der Schnittpunkt S der Seitenhalbierenden (Schwerpunkt des Dreiecks), der Schnittpunkt H der Höhen und der Schnittpunkt M der Mittelsenkrechten (Mittelpunkt des Umkreises) auf einer Geraden liegen (so genannte Eulersche Gerade), wobei die Strecke MH durch den Punkt S im Verhältnis 1 zu 2 geteilt wird.
Und um den Mittelpunkt der Strecke MH kann man einen Kreis zeichnen, der durch die Fußpunkte aller Höhen und Mittelsenkrechten verläuft (Eulerscher Kreis).
Um 1750 findet Euler heraus, dass bei beliebigen konvexen Polyedern für die Anzahl der Ecken e, Kanten k und Flächen f ein einfacher Zusammenhang gilt: e + f – k = 2 (Eulerscher Polyedersatz).
1736 beantwortet Euler die Anfrage des Bürgermeisters von Danzig: Ist es möglich, einen Rundgang durch Königsberg so durchzuführen, dass man dabei jede der 7 Brücken genau einmal überquert? (Königsberger Brückenproblem) In seiner 13-seitigen Lösung legt er dar, warum dies nicht möglich ist, und formuliert ein allgemeingültiges Kriterium, wobei er eine wirklich mathematische Substanz seiner Untersuchung anzweifelt: »Du siehst also, ..., dass diese Lösung ihrem Charakter gemäß kaum Beziehungen zur Mathematik hat, und ich verstehe nicht, warum sie vom Mathematiker eher erwartet werden solle als von irgend einem anderen Menschen, denn diese Lösung stützt sich allein auf die Vernunft und es ist nicht nötig, zu ihrer Auffindung irgendwelche der Mathematik eigenen Prinzipien heranzuziehen.«
Mit diesem Beitrag eröffnet Euler ein neues Gebiet der Mathematik, die Graphentheorie. Heute spricht man allgemein von einem Eulerschen Graphen, wenn bei einem geschlossenen Streckenzug jede Kante (Strecke) genau einmal durchlaufen werden kann. Euler gibt hierzu ein einfaches Kriterium an: Ein Graph ist genau dann ein Eulerscher Graph, wenn an jedem Knoten die Anzahl der Wege geradzahlig ist.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.