Am seidenen Faden

Mathematische Knobelei: Am seidenen Faden

Wer hat eigentlich die Mathematik erfunden? Die Griechen? Die Ägypter? Die Mesopotamier? Alles falsch, behaupten Biomathematiker der University of Middlesix in Ohio, der Natur selbst gebührt die Anerkennung. Als Beweis führen sie ihre Untersuchungen einer erst kürzlich entdeckten Radnetzspinne an, die im April eines jeden Jahres anfängt, in der Prärie ihre Fallen aufzustellen.

Auszug aus Knobelex' Tierleben, Band 42 - Kleinzeugs:

"Pünktlich zum 1. April krabbeln die gestreiften Triangelspinnen (Triangulosa aprilis) aus der Familie der Araneidae aus ihren Erdlöchern hervor und beginnen mit dem Bau ihrer streng geometrischen Fangnetze.

Zunächst errichten sie einen dreieckigen Rahmen mit den Eckpunkten A, B und C, wobei die Spitze A exakt zum Masseschwerpunkt der Erde weist. Anders als die meisten anderen Radnetzspinnen fügen sie anschließend keine Radialfäden zur etwa mittig gelegenen Nabe hinzu. Stattdessen ziehen Triangelspinnen schnurgerade so genannte Triangelfäden von den Ecken B und C auf die jeweils gegenüberliegende Seite.

Erstaunlicherweise gibt die Anzahl n der in je einer Ecke anfangenden Triangelfäden das Alter des Tieres in Jahren an. Offensichtlich verfügen die Spinnen bereits über eine einfache numerische Verschaltung ihres Nervensystems, die ihnen das Zählen erlaubt.

Der Biomathematiker Konrad N. Allkopp vermutet sogar eine noch weitergehende mathematische Begabung. Seinen Beobachtungen zufolge kontrollieren die Spinnen die Gesamtzahl^[1] der Dreiecke in ihrem Netz. Da diese von der Anzahl der Triangelfäden abhängt, müssen die Triangulosae über einen komplexen Neuralalgorithmus verfügen, der ihnen die Berechnung der Dreieckszahl als Funktion von n ermöglicht und eine Abweichung der tatsächlichen Dreieckszahl von diesem Wert bemerkt.

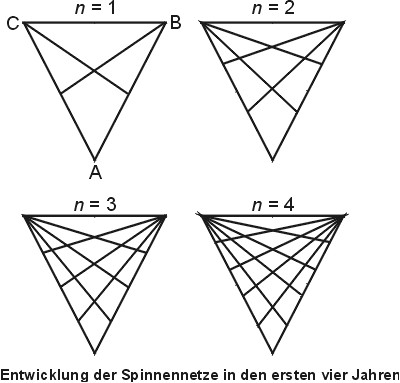
Während diese Aufgabe bei jüngeren Tieren noch durch simples Nachzählen zu bewältigen wäre, müssen ältere Spinnen, deren Lebensdauer nach den bisherigen Forschungsergebnissen durchaus zwanzig oder mehr Jahre erreichen kann, die Sollzahl durch eine Gleichung bestimmen, so Allkopp. Der Wissenschaftler sucht jetzt nach Mitarbeitern, die eine entsprechende Funktion für die Gesamtzahl der Dreiecke aufstellen können. Interessenten melden sich bitte zur Schutzimpfung gegen den überaus schmerzhaften und giftigen Biss der Triangelspinnen in der Abteilung für experimentelle Medizin der University of Middlesix in Ohio."

^[1]Gemeint ist die Zahl aller Dreiecke - auch solcher, die schon als Teil eines größeren Dreiecks gezählt wurden.

Nennen wir die Fäden, die von B ausgehen, B-Fäden, und die, die von C ausgehen, C-Fäden. Der Rahmenfaden, den die Spinne als allererstes von C beziehungsweise B nach A spinnt, zählt dabei mit! (Der Faden BC zählt nicht mit.) Demnach hat das Netz einer n Jahre alten Spinne (n+1) B-Fäden und (n+1) C-Fäden. Jeder B-Faden trifft sich mit jedem C-Faden genau einmal, das macht (n+1)² Schnittpunkte, die Punkte, in denen ein Faden an einem Rahmenfaden (AB oder AC) endet, mitgezählt. Der Punkt A ist in dieser Zählung enthalten, die Punkte B und C nicht.

Es gibt nun drei verschiedene Sorten Dreiecke: – aus einem dieser Schnittpunkte und den Punkten B und C: Das sind (n+1)² Stück. - aus zwei Schnittpunkten, die auf demselben B-Faden liegen, und dem Punkt C. Das sind (n+1) Möglichkeiten, den B-Faden auszuwählen, mal n(n+1)/2 Möglichkeiten, auf diesem Faden zwei Schnittpunkte auszuwählen, macht zusammen n(n+1)²/2 Stück. - aus zwei Schnittpunkten, die auf demselben C-Faden liegen, und dem Punkt B. Das sind noch einmal genauso viele, nämlich n(n+1)²/2 Stück.

Haben wir irgendwelche Dreiecke doppelt gezählt? Nein, denn ein Dreieck kann nicht zwei der drei Sorten angehören: Entweder enthält es den Punkt B, oder C, oder beide.

Haben wir irgendwelche Dreiecke vergessen? Nein, denn eine Figur aus den verfügbaren Linien, die nicht wenigstens B oder C enthält, kann kein Dreieck sein. (Beweis durch scharfes Hinschauen.)

Also können wir die Anzahlen zusammenzählen:
(n+1)² + 2 n(n+1)²/2 = (n+1)(n+1)² = (n+1)³. Also enthält das Netz einer n-jährigen Spinne (n+1)³ Dreiecke.

Das mathematische Problem stammt von Univ.-Prof. Dr. Gerd Baron und Dr. Richard F. Mischak. Weitere Aufgaben finden Sie auf den Seiten des Wettbewerbs Jagd auf Zahlen und Figuren. Die erzählerische "Verpackung" gestaltete Dr. Olaf Fritsche.