(2/3)) = 109,4712 o.
Kelvin vermutete 1887, dass ein Schaum aus Oktaederstümpfen mit leicht gebogenen Kanten stabil sei und größte Zellen bei kleinsten Wandflächen habe. Das wurde 1994 widerlegt.
|
Zu den Stereozeichnungen Schauen Sie entweder überkreuz oder - falls Sie verkleinerte Drucke anfertigen - nahezu parallel mit beiden Augen auf die jeweils zwei Teilbilder, so dass Sie das Bild dreifach sehen. Das mittlere ist dann echt stereoskopisch. Wegen der Durchsichtigkeit der Objekte und der gewählten Fern-Perspektive ist die Zuordnung gleichgültig. Zur Entkoppplung von Akkommodation und Ausrichtung der Augenachsen sind etwas Geduld und Übung nötig und lohnend.
Oberflächenenergie Grenzflächen binden Energie, deren Menge proportional zum Flächeninhalt und zu einer Konstante des jeweiligen Material-Paares ist, hier insbesondere seifenbedecktes Wasser gegen Luft.
Seifenhaut nennt man eine dünne mit Seife oder einem anderen Detergens bedeckte Wasserschicht: Lamelle. Besteht zwischen beiden Seiten eine Luftdruckdifferenz, so ist die mittlere Krümmung proportional zu dieser.
Zur mittleren Krümmung: Man errichtet in einem Punkt einer Fläche ein Lot, also eine Gerade rechtwinklig zur Tangenzialebene, und betrachtet in allen verschiedenen Ebenen, in dem dieses Lot liegt, die Krümmungsradien der Fläche mitsamt einem Vorzeichen, das die Seite des Krümmungsmittelpunkts anzeigt. Die Extremwerte der Kehrwerte dieser Radien sind die Hauptkrümmungen k1 und k2. Deren Produkt ist die - hier nicht interessierende - Gauß-Krümmung. Ihr Mittelwert verschwindet nicht nur für Ebene, sondern auch für gewisse Flächen, die überall sattelartig gewölbt sind.
Ohne solche Druckdifferenz hat die Fläche zwischen festen Umrandungen im stabilen Gleichgewicht ein relatives Minimum des Flächeninhalts: eine Minimalfläche, nicht unbedingt eine Ebene, aber eine Fläche, deren mittlere Krümmung an jeder Stelle null ist und die dabei sattelförmig gekrümmt sein kann.
Treffen mehrere Lamellen an einer Kante zusammen, so sind es im stabilen Gleichgewicht nur drei, und die Winkel zwischen den Flächen sind je 120o, und genau vier Lamellenkanten können sich an gemeinsamen Ecken von sechs Lamellen treffen und dabei vier Zellen trennen, die Winkel sind die gleichen wie in der Mitte eines regulären Tetraeders zwischen den Geraden zu dessen Ecken (Tetraederwinkel , jeweils 2 arcsin((2/3)) = 109,4712 o.
|
Joseph Plateau www.maths.tcd.ie/~simoncox/Foamarchive/gaindexalp.html
So kann man Drahtringe oder Drahtgerüste bestimmter Polyeder in Seifenwasser tunken und herausziehen. Er hat auch einen gemeinsamen Vorfahren des Kinos und des Daumenkinos, das Phenakistiskop erfunden. Als späte Folge von Sonnenbeobachtungen erblindete er.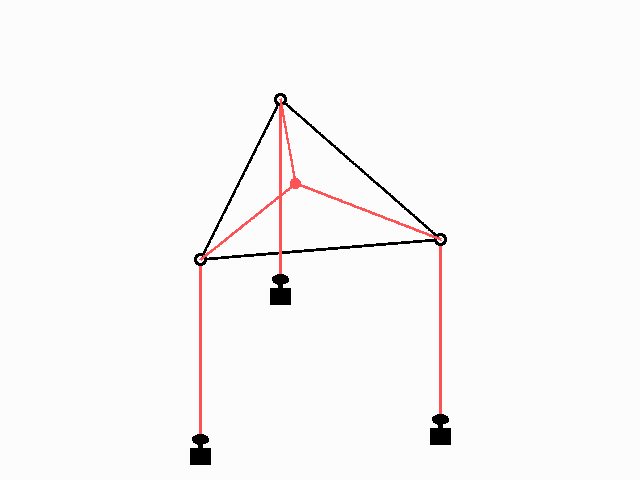
Die Fäden mit den gleichen Gewichten finden den 1. Fermat-Torricelli-Punkt des Dreiecks aus den drei Löchern in der Platte, wenn ihr Haftwiderstand durch Rütteln unwirksam gemacht wird.
Mechanisch kann man das sehr schön demonstrieren mit drei Fäden, die mit an einer Seite zusammengeknotet sind und mit den anderen Enden durch drei Löcher in einer ebenen Platte stecken und dahinter mit drei gleichen Wägestücken belastet sind. Diese Platte muss nicht waagerecht sein, sondern darf auch (fast) senkrecht sein. Rütteln macht den Haftwiderstand in den Löchern unwirksam, und während der gemeinsame Schwerpunkt der Gewichte im homogenen Schwerefeld die tiefste Position einnimmt, also mit der maximalen Summe der unteren Fadenabschnitte, landet der Knoten im gesuchten Punkt. Dort ziehen die drei Fäden im Gleichgewicht, wegen ihrer gleichen Spannungen bilden die Kraftvektoren ein gleichseitiges Dreieck, ihre Richtungen sind also paarweise um 120o verschieden.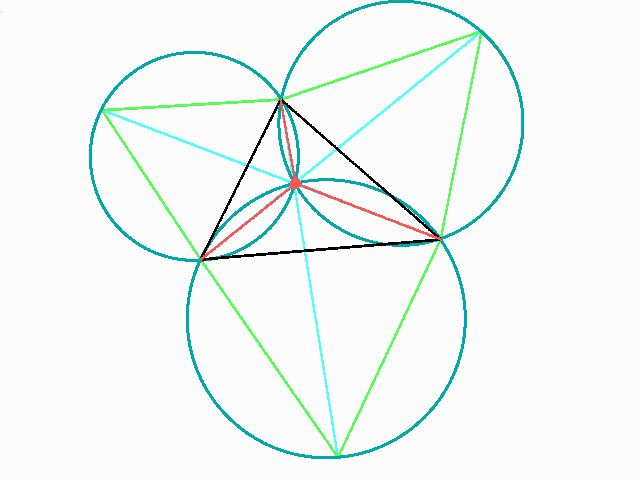
Zeichnerisch finden man ihn mit gleichseitigen Dreiecken und dem Umfangswinkelsatz oder auch mit den hier hellblauen Geraden.
Im gesuchten Punkt schneiden sich wegen des Umfangswinkelsatzes die Umkreise von gleichseitigen Dreiecken, die man an die Seiten des gegebenen Dreiecks außen anfügt. In dieser Form gilt das nur für Dreiecke, in denen kein Winkel stumpfer als 120o ist. Dass diese Teilung des Vollwinkels um die Lamellenkanten in drei gleiche Winkel auch stabil ist, sieht man so ein: Wandert die Kante zufällig (infinitesimal und virtuell) aus ihm in der Ebene einer Lamelle "nach hinten", so wird diese Lamelle etwas kleiner, aber die anderen beiden werden jeweils um halb so viel größer. Sind die Winkel aber ungleich, so ist die Summe der Flächenänderungen negativ, wenn sie sich zur Gleichheit der drei Winkel hin ändern, und größer im umgekehrten Fall. Was interessiert nun das Seifenwasser die Größe der Fläche? Kann ein System Entropie erzeugen, so tut es das, und im Rahmen der Mechanik bedeutet das einfach, Energie über Reibungsprozesse in die weite Welt zu verteilen: Sie kommt dann nicht "von selbst" wieder. Landen wir dabei in einem Zustand, dessen (potenzielle) Energie kleiner als in jedem ereichbaren benachbarten Zustand ist, so sind wir am Ende einer Sackgasse, die zugleich eine Einbahnstraße ist. Dann haben wir ein "stabiles Gleichgewicht", ein bekanntes Beispiel ist ein ruhendes und nicht ausgelenktes Pendel. Im regulären Tetraeder finden die Lamellen sehr schnell die Form, in der sie es vom Mittelpunkt aus in vier flache Tetraeder aufteilen, nämlich mit je 1/4 der Höhe des regulären. Die Außenflächen bleiben leer, so dass keine Druckdifferenz entsteht. Die vier Kanten zwischen den sechs Lamellen treffen sich im Mittelpunkt mit vier gleichen Winkeln, die man Tetraederwinkel nennt und aus der Chemie insbesondere des Kohlenstoffs kennt: Von der Mitte des C-Atoms im Methan bilden die Mitten der H-Atome die Ecken eines regulären Tetraeders und damit vier der acht Ecken eines Würfels. Hat dieser die Kantenlänge k, so hat das gleichschenklige Dreieck HCH die Seitenlänge k sqrt(2) und zweimal (k/2) sqrt(3). 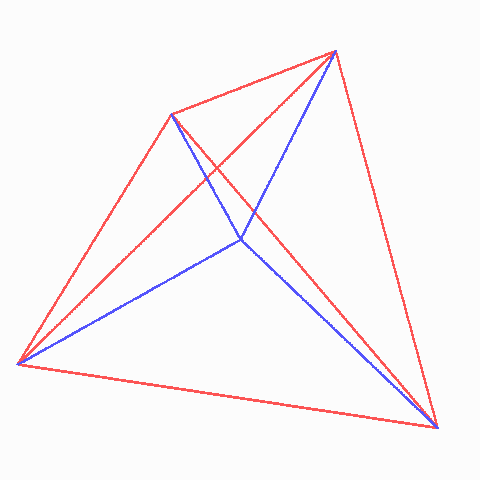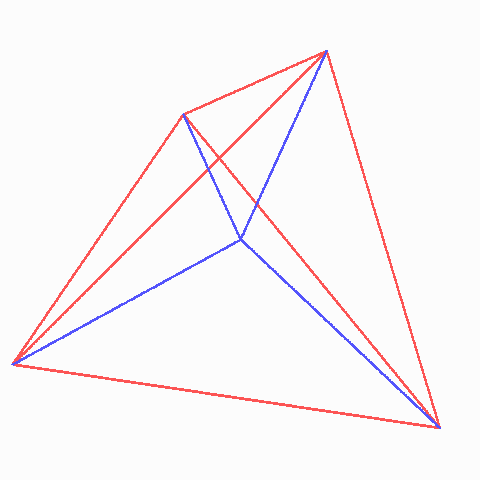Mit einer der Arcusfunktionen findet man dann den Tetraederwinkel (HCH) = 2 arcsin((2/3)) = 109,47122o.
Die sechs Seifenwasser-Lamellen teilen das reguläre rote Draht-Tetraeder in vier gleiche Tetraeder von je 1/4 der Höhe
Wenn man aus Versehen oder absichtlich durch nochmaliges Eintunken eine Luftblase einschließt, so wird diese von vier Kugelstücken begrenzt, die sich und die ebenen Lamellen in Kreisbögen treffen.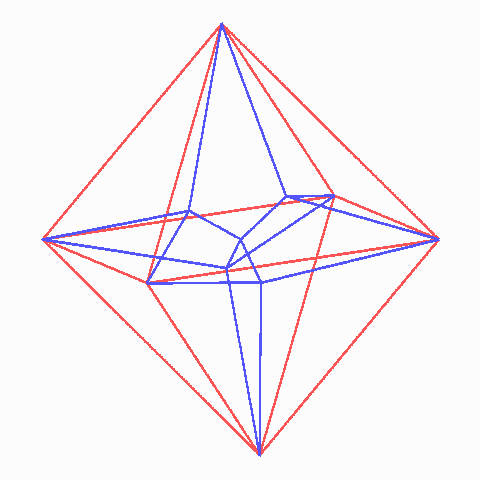
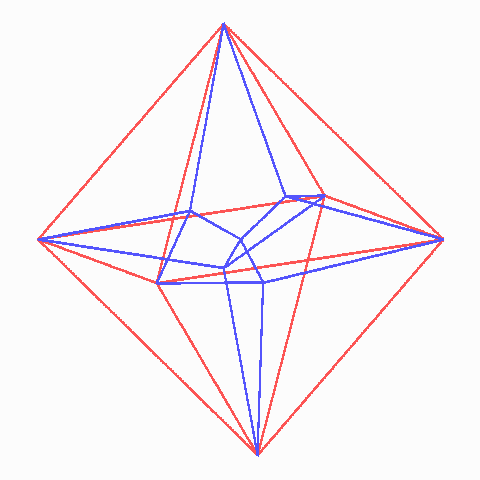
Reguläres Oktaeder (rot) mit 18 Lamellen
Die Lamellenfigur bricht die Symmetrie des regulären Oktaeders und bewahrt nur die des regulären Tetraeders. Dabei teilen sich die acht Flächen in zwei Mengen. Jedes Seite des regulären Oktaeders bildet mit der Mitte ihrer Gegenseite ein reguläres Tetraeder. Dessen Mittelpunkt ist die Mitte zwischen ihrer eigenen Mitte und der des Oktaeders. Von diesen acht Punkten verwenden "wir" nur vier, die die Ecken eines kleinen Tetraeders bilden, dessen Mittelpunkt mit der des ganzen Oktaeders übereinstimmt. So haben wir innen fünf ausgezeichnete Punkte. Die Lamellen bilden nun 12 ebene gleichseitige Dreiecke zwischen ihnen und den Oktaederecken und sechs ebene Drachenvierecke zwischen ihnen und den Ecken des Oktaeders. Alle Winkel zwischen zwei Lamellen sind 120o, und alle Winkel zwischen Lamellenkanten an den fünf Punkten haben den Wert des Tetraederwinkels. Das ganze Oktaeder wird von den Lamellen in vier flache Tetraeder und vier ebenfalls untereinander deckungsgleiche Polyeder aufgeteilt, die sehr hübsche Zelte abgäben, wenn man sie hinreichend groß baute.
Es gibt im regulären Oktaeder auch eine Figur mit einem Sechseck in der Mitte, das aber nicht eben ist, sondern leicht im Sinne eines Affensattels gewölbt ist.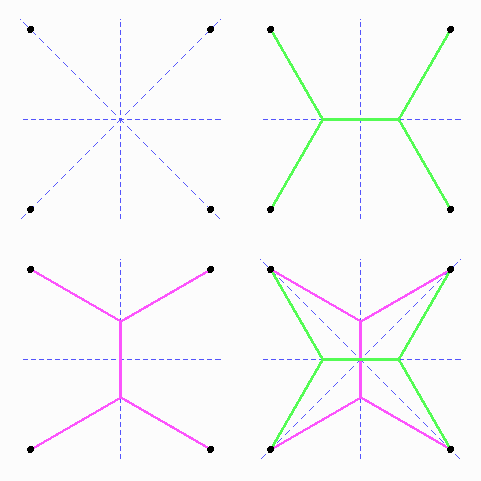
Links oben die vier Ecken und ihre vier Symmetrie-Geraden, außerdem besteht Punktsymmetrie für Vierteldrehungen. Die beiden Lösungen rechts oben und links unten haben nur Halbdrehungssymmetrie und nur zwei Symmetriegeraden. Erst die Überlagerungen beider Lösungen rechts unten zeigt die volle (Quadrat-) Symmetrie der Aufgabenstellung.
Ein Kreuz aus den beiden Diagonalen ist schon einmal nicht schlecht, aber das Netz wird noch kürzer, wenn wir statt eines Kreuzungspunktes in der Mitte unter Brechung der Symmetrie zwei Verzweigungen einbauen, an denen es jeweils dreimal 120o gibt, die Figur sieht dann wie ein Mittelding zwischen einem H und einem X aus. Zusammen mit der anderen Lösung hat die Figur wieder die volle Symmetrie des Quadrats, also vier Spiegelgeraden statt nur zweier und Vierteldrehungen um den Mittelpunkt statt der Halbdrehung. In zwei Dimensionen sind Zweigpunkte mit drei Strecken und gleichen Winkeln stabil, solche mit vier Strecken (wie z.B. Kreuzungen) dagegen instabil. Nun kehren wir zum Würfel zurück. In seiner Mitte treffen sich sechs Pyramiden statt nur vier in der Tetraedermitte, und es sind zwölf Lamellen statt nur sechs. Das schreit nach Umbau zugunsten von mehr Spitzen mit Tetraedermitten-Struktur, ohne zuviel Rücksicht auf die Symmetrie. Analog zum ebenen Quadrat bauen wir Verzweigungsopunkte ein, und zwar die Ecken eines Quadrates, das zusammen mit zwei gegenüberliegenen Würfelseiten, vier Dreiecken und acht Trapezen den Würfel in zwei Pyramidenstümpfe und vier Dachfiguren mit den Quadrateseiten als Firststrecken aufteilt. Bei passender Größe des Quadrats können seine Seiten dabei die Winkel von je 120o bekommen. Das sieht so gut aus, dass viele Autoren das schon für die ganze Wahrheit halten (ich leider früher auch!). Dummerweise bekommen aber nun gerade durch den Einbau des Quadartes die Lamellenkanten, die von innen zu den Würfelecken laufen, ungleiche Winkel zwischen den Lamellen. Außerdem sind die rechten Winkel des Quadrats natürlich keine Tetraederwinkel, was sie aber sein sollten. Das Seifenwasser im Würfel weiß sich aber zu helfen: Die Kanten des Quadrats krümmen sich nach außen und vergrößern dabei die Winkel zwischen sich. Die anderen Kanten krümmen sich ebenfalls, und die zwölf Lamellen, die zu den Würfelkanten reichen, wölben sich zu nicht-ebenen Flächen mit trotzdem verschwindender mittlerer Krümmung an jeder Stelle. Für ein so einfaches Gerüst wie einen Würfel ist das ganz schön raffiniert, ganz anders als die bestechend schlichte Eleganz der 18 ebenen Lamellen im Oktaeder.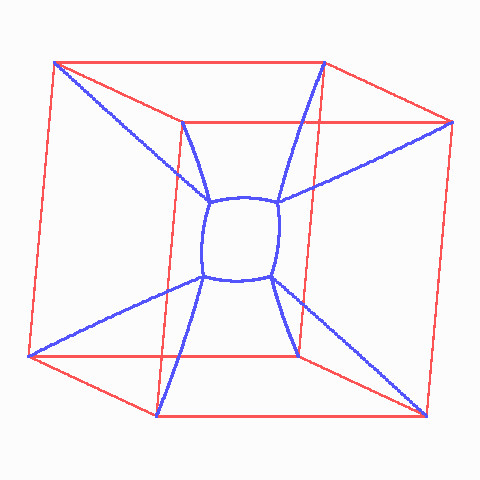
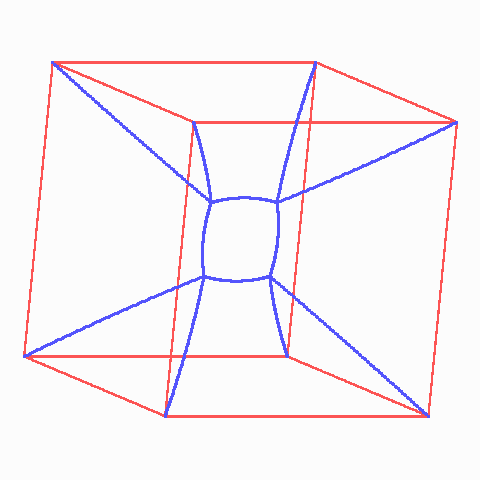
Lamellen im Drahtwürfel. Die Symmetrie wird durch das Bogenquadrat in der Mitte gebrochen. Der Würfel wird von den 13 Lamellen annähernd in vier Dächer und zwei Pyramidenstümpfe zerlegt.
/4 = 78,4 % gegen 74 %). Wenn man viel Volumen V mit wenig Oberfläche O verpacken will, so ist der dimensionsfreie Faktor 36 V2/O3 = "isoperimetrischer Quotient", kurz IPQ, ein gutes Maß, er ist für die Kugel = 1 (nämlich mit dem Faktor 36 passend gemacht) und für den Würfel /6 = 52,36 %.
Nun geht es bei dem Würfel nicht mehr darum, Lamellen hineinzuziehen, sondern den unbegrenzten Raum mit gleichen Exemparen zu füllen, deren Wände dabei die Lamellen bilden.
Im Gegensatz zum regulären Tetraeder und zum regulären Oktaeder ist der Würfel tatsächlich ein Raumfüller. An den Ecken treffen sich aber immerhin je acht Zellen, zwölf Lamellen und 6 Kanten, also in jeder Hinsicht entschieden zu viele, das Würfelgitter ist also als Schaum nicht stabil, und man könnte überlegen, die Würfel abzustumpfen und in die Ecken Oktaeder zu setzen.
Wir wollen aber die Forderung stellen, dass alle Zellen von gleicher Sorte und Größe sein sollen.
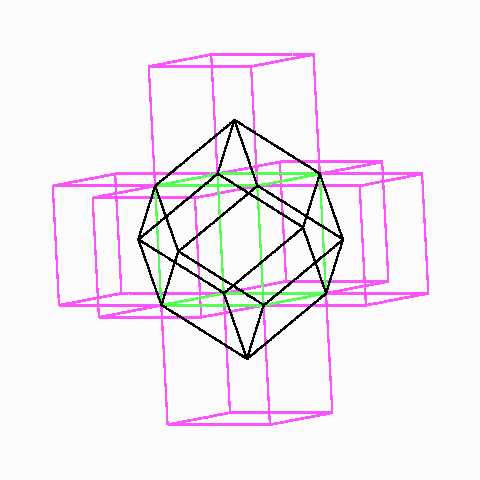
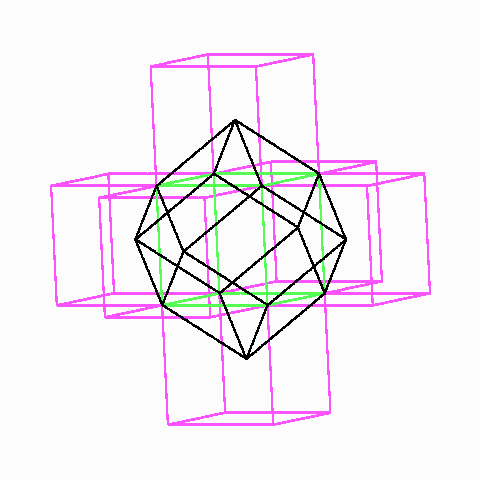
Das catalansche Rhombendodekaeder mit sieben Würfeln, von denen einer ganz und sechs zu je einem Sechstel in ihm liegen. Es ist die Wigner-Seitz-Zelle des fcc-Gitters.
Reguläre und halbreguläre konvexe PolyederEin Polyeder ist konvex, wenn alle Strecken zwischen zwei seiner Punkt ganz zu ihm gehören (wenn er also insbesondere keine Talfalten oder Hohlräume hat). Eckenäquivalenz bedeutet, dass man bei einer Drehung, die eine Ecke in gleicher Orientierung an die Stelle einer beliebigen anderen bringt, das ganze Polyeder mit seiner bisherigen Gestalt zur Deckung bringt. Eckenäquivalente Polyeder mit einheitlicher Kantenlänge haben je eine Kugel durch alle Ecken (Umkugel) und eine, die alle Kanten berührt (Kantenkugel). Ganz analog ist Flächenäquivalenz definiert, sie zieht die Existenz einer Inkugel, die alle Flächen berührt, und ebenfalls einer Kantenkugel nach sich, sowie die Eignung als "fairer Würfel". Die fünf platonischen Polyeder sind zugleich konvex, ecken- und flächenäquivalent. Zusammen mit gewissen vier nicht-konvexen Sternpolyedern (die von Kepler und Poinsot gefunden wurden) nennt man sie regulär. Es gibt abzählbar unendlich viele eckenäquivalente Prismen aus zwei regulären n-Ecken und n Quadraten und ebenso viele ebensolche Antiprismen aus zwei regulären n-Ecken und 2n gleichseitigen Dreiecken. Außer diesen Prismen, Antiprismen und konvexen regulären Polyedern gibt es 13 weitere eckenäquivalente konvexe Polyeder, sie sind nach Archimedes benannt. Zu jedem eckenäquivalenten gibt es ein flächenäquivalentes Polyeder (Dualität), man kann die zueinander dualen so skalieren und orientieren, dass sie eine einzige Kugel als gemeinsame Kantenkugel haben dass die Kantenberührpunkte des einen mit denen des anderen zusammenfallen. Zu den Prismen sind entsprechende Doppelpyramiden, zu den Antiprismen passende Drachenvielflache dual (oft Trapezoeder, besser Deltoeder genannt, im Unterschied zu den Deltaedern, die nur gleichseitige Dreiecke als Flächen haben und von denen es genau acht konvexe gibt). Die platonischen sind paarweise zueinander dual, das Tetraeder im strengen Sinn ("kanonisch dual") zu seinem eigenen (Punkt-) Spiegelbild. Die 13 zu den archimedischen dualen werden nach Catalan benannt. Die genannten halbregulären und regulären konvexen Polyeder kann man nach Cundy und Rollett durch Ecken- bzw. Flächenformeln kennzeichnen: 4.6.6 bedeutet, dass sich an jeder äquivalenten Ecke ein Viereck und zwei Sechsecke treffen, bei dem dazu dualen Tetrakishexaeder bedeuten die gleichen Zahlen, dass jedes der gleichen Polygone eine vier- und zwei sechszählige Ecken hat. |
(2) als langer. Es hat die Oberfläche 12 k2 (1/2) und das Volumen 2 k3. Der IPQ
des catalanschen Rhombendodekaeders ist also 0,7405. Diese Zahl ist genau gleich dem Raumfüllungsfaktor für die fcc-Packung (fcc = flächenzentriert-kubisch) von Kugeln, deren Wigner-Seitz-Zelle das genannte Rhombendodekaeder ist, aber diese Übereinstimmung lässt sich nicht auf andere Polyeder verallgemeinern.
Wenn es nämlich so wäre, würden wir für den archimedischen Oktaederstumpf, der ja die WSZ des bcc-Gitters mit nur 68 % ist, einen schlechteren Wert erwarten.
Die fcc-Packung aus catalanschen Rhombendodekaedern hat überall 120o zwischen den Wänden, besser könnte es nicht sein, aber es treffen sich je zwölf von ihnen in gemeinsamen Ecken, nämlich genau wie in den Mitten des Drahtwürfels, wenn das zentrale Quadrat nicht auftreten würde. Das catalansche Rhombendodekaeder ist zwar rechnerisch ziemlich gut, aber nicht stabil.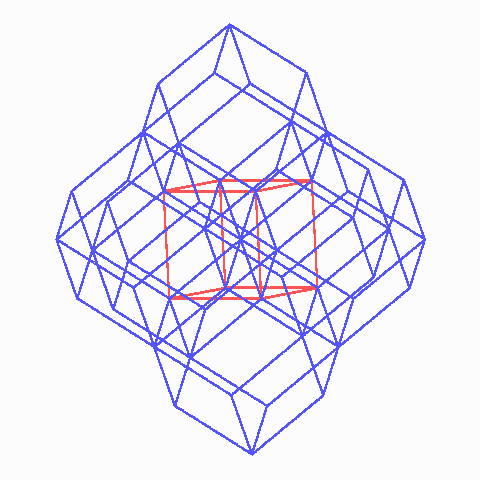
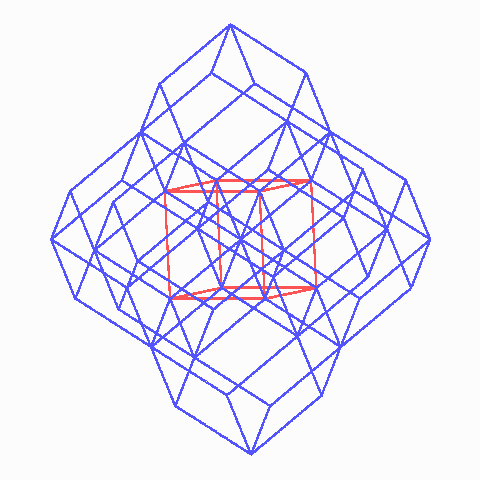
Im fcc-Gitter treffen sich die spitzen Ecken der Rhombendodekaeder zu sechst, wobei zwölf Rauten in gemeinsamen Ecken koinzidieren.
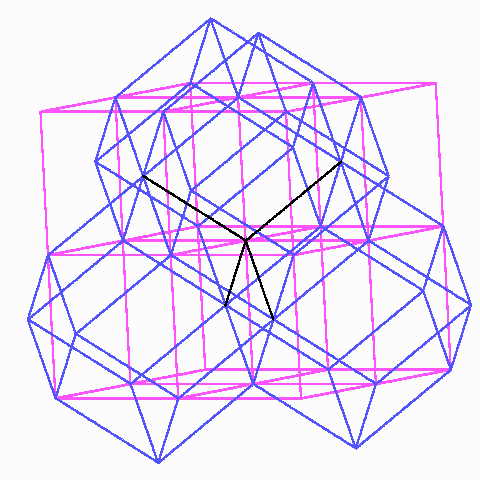
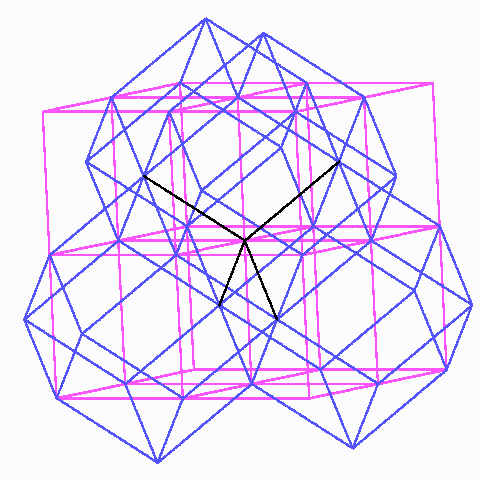
Die stumpfen Ecken treffen sich dagegen wie die Viertel eines regulären Tetraeders, nämlich zu viert mit sechs Rauten.
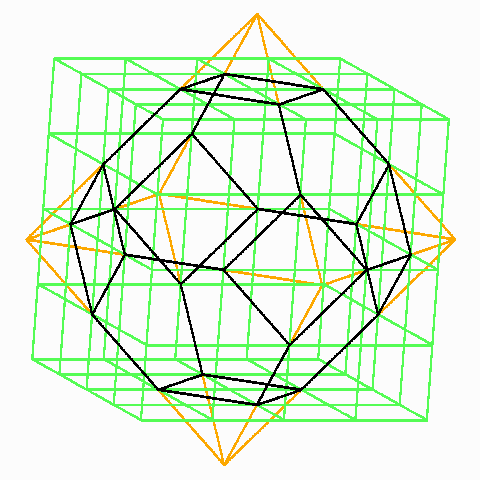
Der archimedische Oktaederstumpf als Schnitt aus Würfel und regulärem Oktaeder
Dieses auf den ersten Blick recht gewöhnliche Polyeder wartet mit einer Fülle von Besonderheiten auf, die zum Teil mit seiner Eigenschaft als Raumteiler und als Wigner-Seitz-Zelle des bcc-Gitters (bcc = raumzentriert-kubisch) zusammenhängen. Das ist auch der Grund, warum er hier beim Schaum interessant ist. Wir schneiden einen Würfel der Kantenlänge 4 a mit einem regulären Oktaeder der Diagonalenlänge 6 a in der im Bild gezeigten Orientierung. Der Schnitt ist ein archimedisches Polyeder und hat die Eckenformel 4.6.6, d.h. an jeder der 24 zueinander äquivalenten Ecken treffen sich ein Quadrat und zwei regelmäßige Sechsecke. Seine Kanten haben die Länge k(2), also 1/3 von der des Oktaeders.
Ecken-Äquivalenz bedeutet nicht nur Kongruenz der Umgebungen aller Ecken, sondern darüber hinaus, dass man das Polyeder so drehen kann, dass eine Ecke den Platz einer beliebigen anderen einnimmt und das ganze Polyeder dabei mit seiner alten Figur zur Deckung kommt.
Zusatzbemerkung hierzu: Darin liegt der Unterschied zwischen dem Miller-Polyeder und dem archimedischen Kleinen Rhombikuboktaeder 3.4.4.4
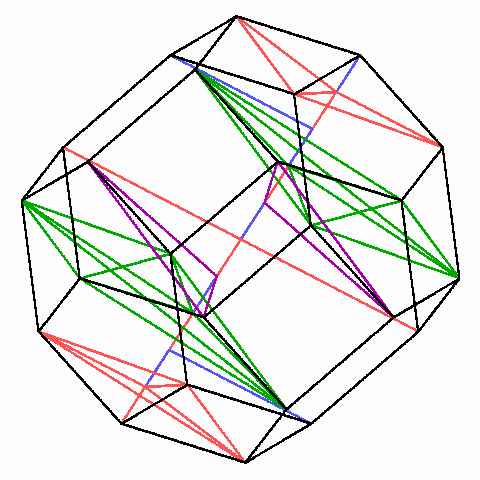
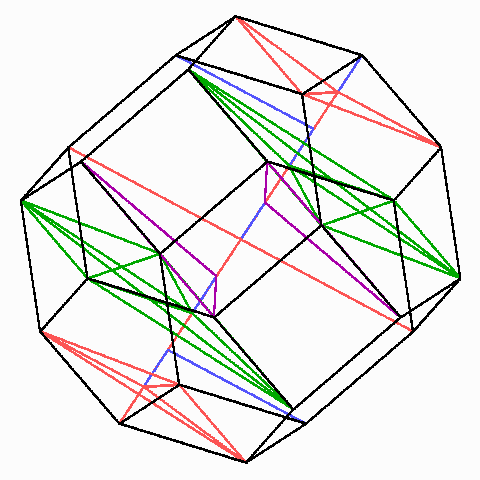
Alle Diagonalen im Oktaederstumpf haben die Längen a(2 n) = k(n) mit allen n von 2 bis 10. Das kann man im Stereobild leicht mit dem pythagoreischen Satz nachvollziehen, wobei wegen der Äquivalenz der Ecken die 23 Diagonalen von einer Ecke aus genügen.
Aus diesen Längen ergeben sich der Durchmesser der Umkugel k(10) und der der Kantenberührkugel 3 k. Stapelt man die Stümpfe raumfüllend, so gibt es ein bcc-Gitter mit k(8) als Gitterkonstante. Die größte Kugel, die hineinpasst, indem sie die Sechsecke berührt, hat den Durchmesser k(6). In den Würfel passen 1 + 8/8 = 2 solche Kugeln. Daraus ergibt sich der bcc-Kugelfüllungsfaktor 0,68.
(3/4), das macht für den isoperimetrischen Quotienten 0,75336, also etwas besser als bei dem zuvor betrachteten Rhombendodekaeder.
Elf gleichabständige Ebenen durch alle Ecken des archimedischen Oktaederstumpfs
Aus der Existenz der Umkugel und der erwähnten Abstufung der Diagonalenlängen folgt mit Thales und Pythagoras, dass es zwölf Scharen von je 11 zueinander parallelen und gleich-abständigen Ebenen gibt, in denen jeweils alle 24 Ecken liegen, nämlich zu jeder der zwölf Diagonalen durch den Mittelpunkt eine Schar.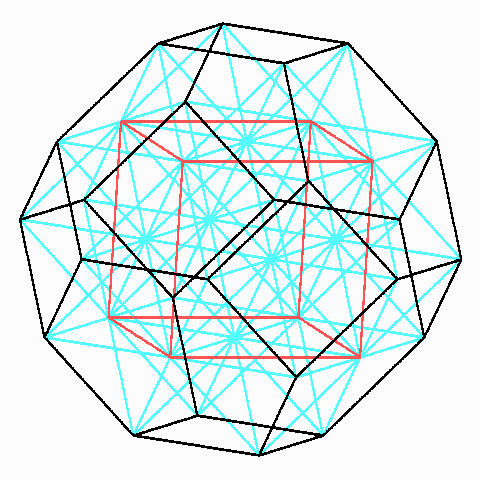
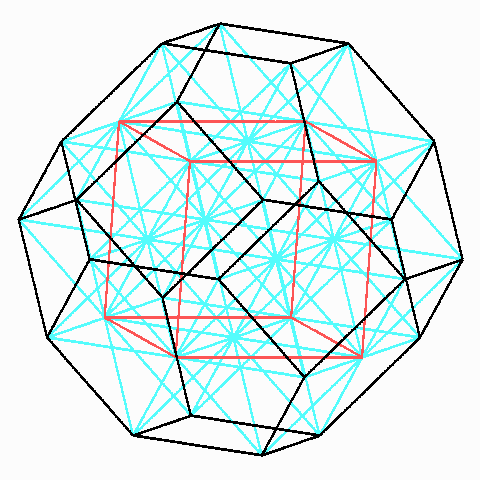
fcc-Gitter aus Ecken und Sechseckmitten des archimedischen Oktaederstumpfes
Seine Ecken und die Mitten der Sechsecke bilden ein fcc-Gitter, das die Grundlage für viele Puzzle-Spiele liefert, darunter auch Kugelpuzzles und Spiele mit (gleich-langen) Stabmagneten und Kugeln. So kann man ihn aus 1 + 6/2 regulären Oktaedern und acht halben archimedischen Kuboktaedern zusammensetzen: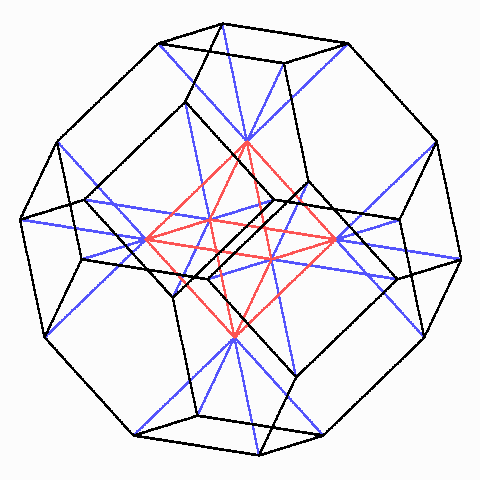
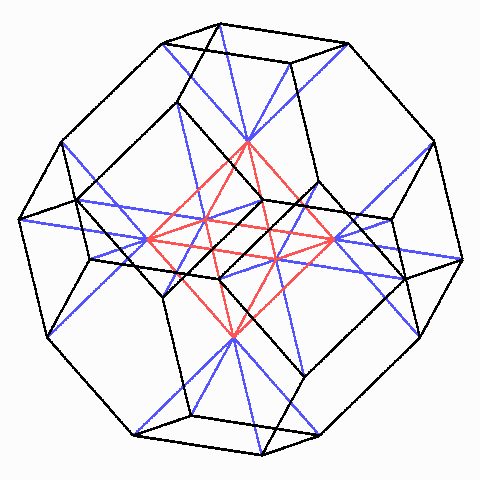
Zerlegung des archimedischen Oktaederstumpfes in acht halbe reguläre Oktaeder und acht halbe archimedische Kuboktaeder
Daraus folgt auch, dass solche Oktaeder und ebenso viele Kuboktaeder (oder statt dessen auch Würfelstümpfe) gemeinsam den Raum füllen können, nicht aber eine dieser Sorten einzeln. Durch Weglassen einzelner Kuboktaederhälften ("Kuppeln") kann man auch nach Bonnie Madison Stewart sehr reizvolle toroidale Polyeder mit Tunneln herstellen.
1. Baron Kelvin of Largs www.maths.tcd.ie/~simoncox/Foamarchive/gaindexalp.html
Nun verlassen wir das überaus reichhaltige Innenleben des Oktaederstumpfes und kehren wieder zu seiner Verwendung als Seifenhaut-Zelle und ins Jahr 1887 zurück zu Kelvin, der noch immer Sir William ist. Seine Nichte traf den 63-Jährigen eines Tages bei einem Besuch mit Seifenblasen spielend an. Er hatte auch ein matratzenähnliches Gitter aus Drähten gebaut, das die Uni Glasgow als "Kelvin's bedspring" in Ehren hält.
www.maths.tcd.ie/~simoncox/Foamarchive/gaindexalp.html
Kelvin nannte den Oktaederstumpf "tetrakaidecahedron", also Vierzehn-Flächner, aber er wusste von Plateaus Versuch mit dem Drahtwürfel, dass es mit minimaler Fläche nicht getan sein muss, wenn man bei Geraden und Ebenen bleibt. Was tut nun der Schaum aus Oktaederstumpf-Zellen? Diese Zellen treffen sich zu viert in den Ecken, wenn auch nicht genau mit den optimalsn Winkeln. An den Kanten treffen sie sich zu dritt, aber die Winkel zwischen zwei Sechsecken sind um etwa 10 Grad zu klein, und die zwischen einem Quadrat und einem Sechseck um etwa 5 Grad zu groß.Das kann man so ausrechnen: Man betrachtet rechtwinklige Dreiecke mit dem rechten Winkel in der Mitte eines Quadrats oder aber eines Sechsecks und der Mitte eines Kante sowie der Mitte des ganzen archimedischen Oktaederstumpfes als weiteren Ecken, und lässt darauf eine der Arcus-Funktionen los. Der Winkel zwischen den Sechsecken ist genau gleich dem Tetraederwinkel, obwohl der ja im regulären Tetraeder nicht zwischen Flächen, sondern zwischen Geraden vorkommt.
Zusammen gibt es zu dritt genau 360o, aber wenn die Seiten der Quadrate sich in deren Ebenen nach außen ausbeulen, ganz ähnlich wie beim Quadrat im Drahtwürfel, werden die Lamellen insgesamt etwas kleiner. Die 36 Kanten eines einzelnen archimedischen Oktaederstumpfs zerfallen zwar trotz gleicher Längen in zwei Klassen: zwölf zwischen je zwei Sechsecken stammen sozusagen noch von dem Oktaeder, bevor es abgestumpft wurde, und die anderen 24 entstehen erst beim Abstumpfen zwischen je einem Quadrat und einem Sechseck. Im (bcc-) Gitter, das mit diesen Oktaederstümpfen vollgestapelt ist, gibt es dagegen nur noch eine Sorte von Kanten, jede liegt zwischen zwei Sechsecken und einem Quadrat und hat daher einen zu kleinen und zwei zu große Winkel zwischen den Ebenen, und rund um die Kante herum addieren sich die ungleichen Winkel zu 360o.
In einer Würfelzelle des bcc-Gitters sitzt ein archimedischer Oktaederstumpf in der Mitte ("body centered"), je 1/8 an jeder Ecke.
Die Sechsecke liegen in Spiegelebenen zwischen nächsten Nachbar-Atomen, die Quadrate in solchen zwischen zweitnächsten Nachbarn. Die Spiegelebenen zwischen den nächsten Nachbarn bilden Oktaeder, die sich gegenseitig durchdringen, die zwischen zweitnächsten bilden die gezeichneten Würfel, die per saldo je zwei Atome enthalten, nämlich 1 ganzes und 8 Achtel.
Mit den Tetraederwinkel-Kreuzen aus einem Chemiebaukasten und Schlauchstücken ergeben sich die Verbiegungen fast von selbst
www.maths.tcd.ie/~simoncox/Foamarchive/gaindexalp.html
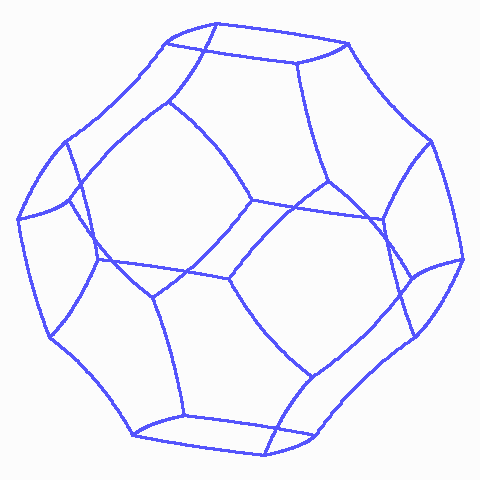
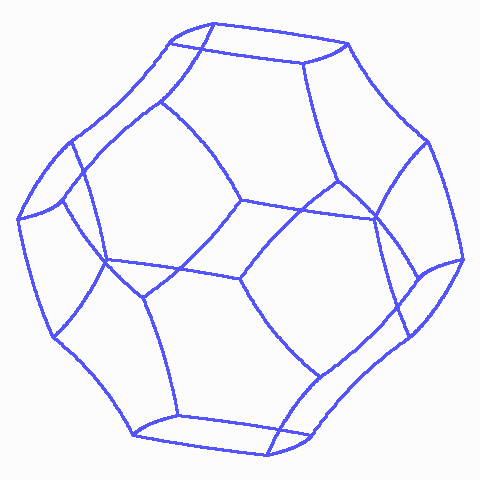
Am einzelnen Oktaederstumpf gibt es zweierlei Kanten, zum einen die Seiten von Quadraten: Sie sind in deren Ebenen von deren Mittelpunkten weg nach außen verbogen. Die Kanten zwischen zwei Sechsecken sind dagegen zur Mitte des Polyeders verbogen.
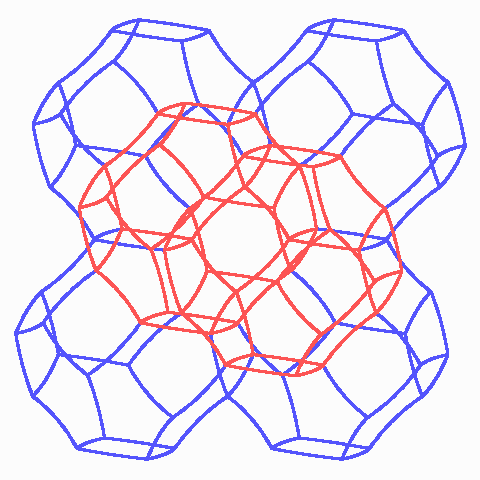
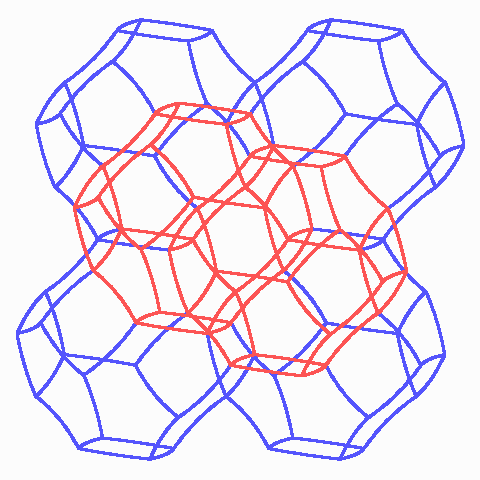
Sechs Kelvin-Zellen. Jede Kante liegt an einem Bogenquadrat und zwei unebenen Sechsecken, es gibt also im ganzen Gitter nur eine Sorte von Kanten.
Der IPQ wird dabei zu 0,757, also besser als alles, was wir bisher bei Raumfüllern bekommen haben (die Kugel gehört nicht dazu und wird nur zur Normierung des IPQ benutzt), und es gibt auch keinen offensichtlichen Grund zur Instabilität. Kelvin war davon überzeugt, dass idealer Schaum aus diesen Beinahe-Polyedern aufgebaut sein muss. Berühmte Vermutungen in der Mathematik werden oft nach beachtlich langer Zeit bewiesen (Fermat, Vier-Farben, fast auch Kepler), gelegentlich aber auch widerlegt. Mit Kelvins Vermutung geschah das Letztere bereits nach 107 Jahren, wenn man einmal davon absieht, dass die Existenz von Flugzeugen und der Erfolg des Radios auch gewissermaßen Widerlegungen von Vermutungen Kelvins sind, die allerdings wesentlich früher eingetreten sind.
Denis Weaire und Robert Phelan
www.maths.tcd.ie/~simoncox/Foamarchive/gaindexalp.html
www.maths.tcd.ie/~simoncox/Foamarchive/gaindexalp.html
(21) und eine längere mit 6 Einheiten hat, wobei die zu dieser parallelele Diagonale die Würfelkante mit der Länge 8 ist. Dieses Dodekaeder hat also immerhin allesamt (zwölf) deckungsgleiche Fünfecke und zweierlei Kantenlängen, nämlich die sechs langen als Dachfirste und die 24 kürzeren von den acht Würfelecken aus zu dritt. Von der Symmetrie des Würfels sind immerhin die vier dreizähligen Drehachsen (durch die Raumdiagonalen) und drei der neun Spiegelebenen, nämlich die zu den Quadraten parallelen, bewahrt. Man kann es auf zwei Arten so in einen Würfel stellen, dass die Dachfirste parallel zu dessen Kanten sind. Diese beiden Arten unterscheiden sich um eine Vierteldrehung um eine der Halbdrehungsachsen, die mitten durch zwei Firste gehen.
Dieses Pentagon-Dodekaeder unterscheidet sich vom regulären (platonischen) dadurch, dass die Fünfecke bei letzterem regelmäßig sind und bei Längen und Koordinaten mehrfach den goldenen Schnitt aufweisen. Auch bei ihm treten Würfel zwischen den Ecken auf, aber nicht nur bei einem Satz von acht Ecken, sondern von jeder Ecke aus auf zwei Weisen.
Zu diesen etwas unregelmäßigen Dodekaedern gesellt sich nun die dreifache Menge von 14-Flächnern (vornehm, aber ebenso wenig ins Detail gehend: Tetrakaidekaeder) mit je zwei Sechsecken und zwölf Fünfecken. Die beiden Sechsecke sind ungleichseitig, aber in parallel zu einander liegenden Ebenen, wenn auch um einen rechten Winkel gegeneinander verdreht.
Von den zwölf Fünfecken sind vier identisch mit solchen der genannten Dodekaeder, die anderen acht sind ebenfalls untereinander deckungsgleich und in sich klappsymmetrisch.
Außer den beiden verschiedenen Kantenlängen des Dodekaeders treten somit noch zwei weitere an ihm auf.
Wir haben also bei beiden Sorten von Polyedern insgesamt vier verschiedene Kantenlängen, aber nur drei Sorten von deckungsgleichen Flächen, nämlich das Sechseck und zwei klappsymmetrische Fünfecke.
Das Tetrakaidekaeder hat zwei Spiegelebenen, und zwar durch die Mittelpunkte der Sechsecke.
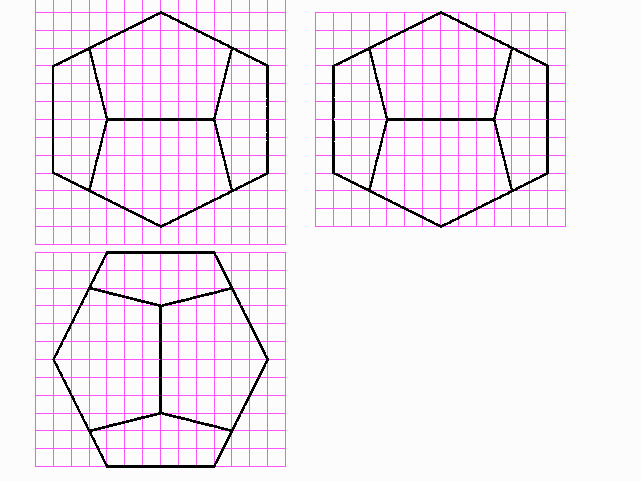
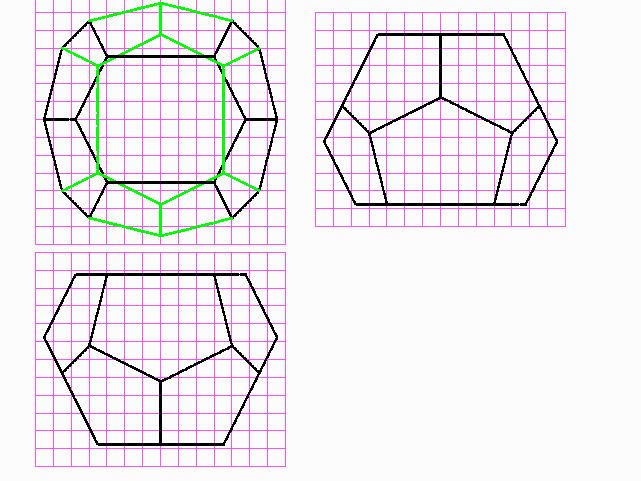
Dreitafelbilder der beiden Phelan-Weaire-Polyeder
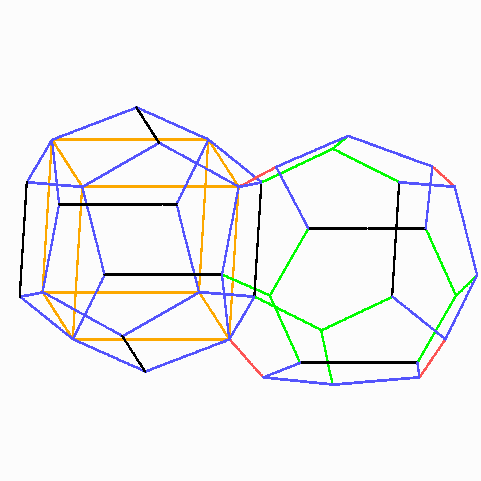
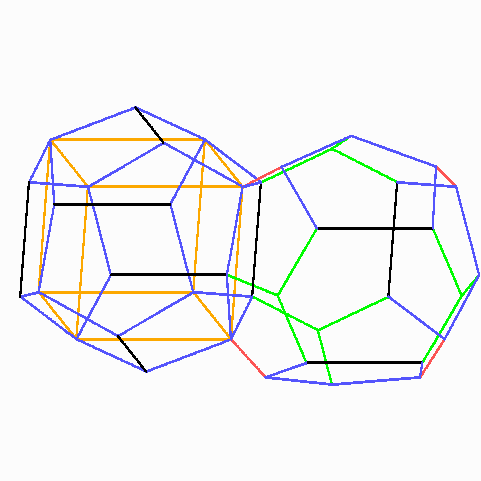
Die beiden verschiedenen Polyeder des Phelan-Weaire-Schaums. Gleiche Farben bedeuten gleiche Kantenlängen. In das Dodekaeder ist orange ein Würfel eingezeichnet, um dessen Symmetrie zu verdeutlichen.
Wenn man sich auf ein kubisches Gitter bezieht, so gibt es für das Dodekaeder zwei und für das Tetrakaidekaeder sechs bevorzugte Orientierungen. Im kubischen Translationsgitter des Phelan-Weaire-Schaums kommen diese acht je genau einmal vor, und zwar die Dodekaeder an den Ecken und in den Mitten eines Würfels, und die anderen als Spiegelbildpaare zu je zweit mit ihre paarweisen Mittelpunkten in den Flächenmitten. Das Ganze ist also gar nicht so unregelmäßig wie es auf den ersten Blick scheint. Ob dieser Schaum nun theoretisch optimal ist, weiß man nicht. Man weiß auch nicht, ob wenigstens unter den gleichzelligen Schäumen der von Kelvin (und unter den verbiegunsfreien der Oktaederstumpf) der beste ist. Wie die Geschichte zeigt, muss man da sehr vorsichtig sein.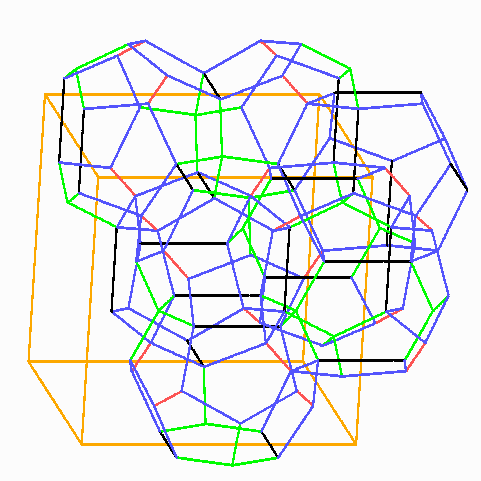
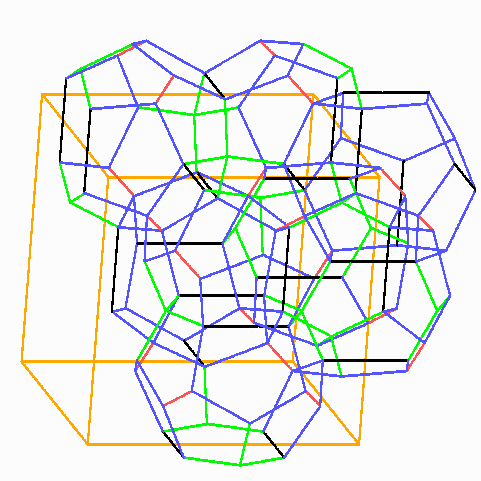
In jeder Würfelzelle (orange) sitzen zwei deckungsgleiche Dodekaeder mit den langen Kanten parallel zu denen des Würfels, und zwar in beiden verschiedenen Orientierungen, eins in der Mitte und eins zu je einem Achtel in den Würfelecken.
Die sechs Tetrakaidekaeder bilden zu zweit Spiegelpaare auf den Flächen dieses Würfels mit den paarweisen Mittelpunkten in deren Mitten, in insgesamt sechs Orientierungen, nämlich drei für die Paare. Zur besseren Übersicht sind hier erst einmal die beiden Typen der Polyeder getrennt gezeichnet: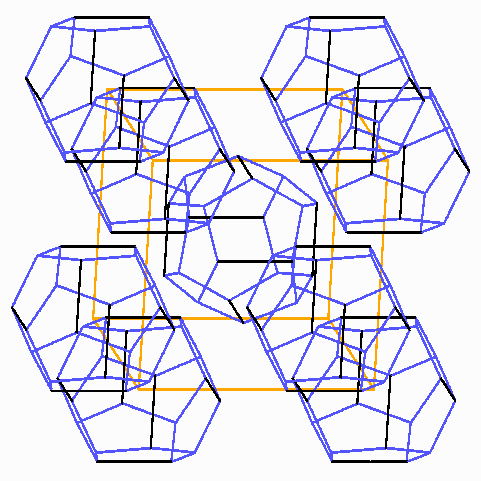
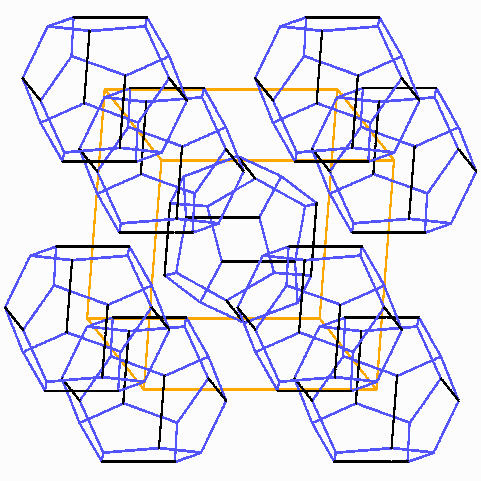
Die Dodekaeder bilden ein bcc-Gitter: eins in der Mitte und 8/8 an den Ecken gehören zu dem Würfel.
Dabei lässt sich nicht vermeiden, dass auch das zentrale Dodekaeder geschlossen zu sehen ist, obwohl es in diesem Bild gar nicht gemeint ist: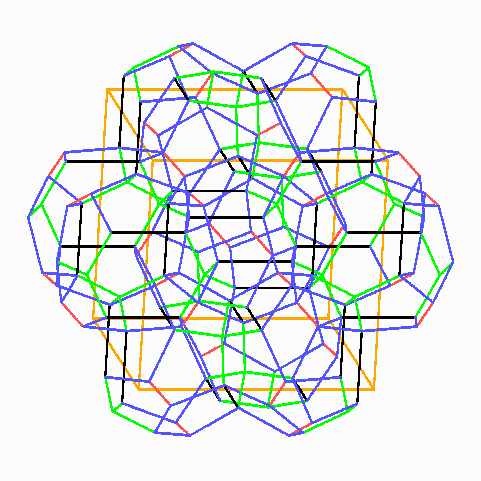
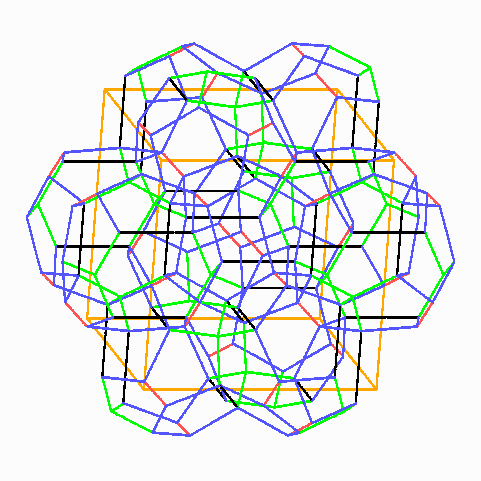
Diese 12 Tetrakaidekaeder gehören jeweils zur Hälfte zu dem Würfel, sie begrenzen das Dodekaeder in der Mitte vollständig.
Alles zusammen sieht dann so aus: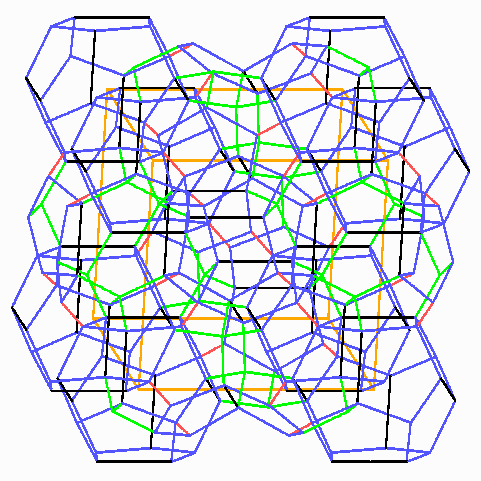
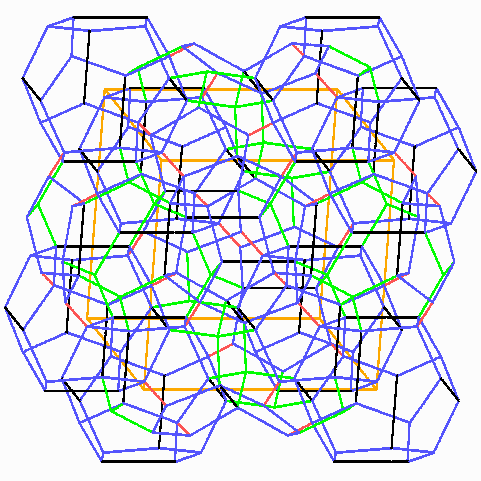
21 Zellen, deren Mitten in oder an einem Translationswürfel liegen: die Zellen auf den Ecken gehören nur zu je 1/8 zu dem Würfel, die zwölf auf den Flächen je zur Hälfte. Ohne die vorangegangenen Bilder könnte man hier glatt die Übersicht verlieren!>
Die Verbindung aus den acht Zellen ist ein raumfüllendes Polyeder, da der Raum mit deckungsgleichen Kopien von ihm gefüllt werden kann. Im Sinne des Schaums sind das aber trotzdem acht Zellen und nicht eine, weil ja auch die inneren Wände an der Energie beteiligt sind und bei der Optimierung mitspielen. Und so hat sich Chris Smith die Entdeckung vorgestellt, frei nach Archimedes und vermutlich ohne Kenntnisse über die Herren Dr. Klöbner und Müller-Lüdenscheid, die uns durch Loriot bekannt sind:
www.math.tcd.ie/~wiebke/DRAWING/FOAMS/foams.htm