Die Covid-19-Pandemie hat die Virologie zum Dauerthema in den Medien gemacht – aber auch die Mathematik. Das exponentielle Wachstum der Infektionsfälle nämlich ist, was die Situation so Besorgnis erregend macht: Die Anzahl der Infizierten verdoppelt sich immer nach dem gleichen Zeitraum.

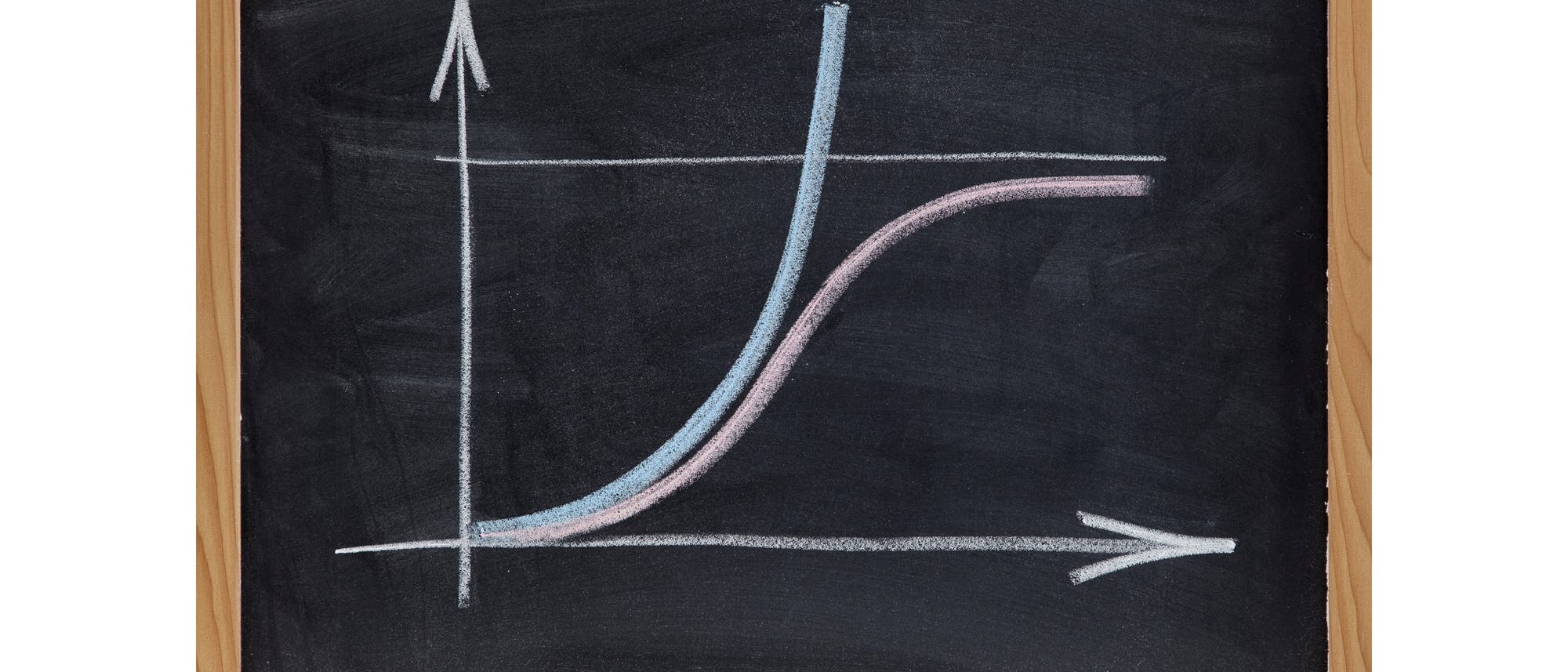
Das sieht anfangs noch harmlos aus, führt aber erschreckend schnell zu ebenso erschreckend großen Zahlen. Deswegen trifft man Maßnahmen, um die Ausbreitung einzuschränken. Dadurch will man das exponentielle Wachstum bremsen und die ständig schnell ansteigende Kurve der Infektionsfälle in eine Form »biegen«, die durch eine andere Gleichung beschrieben wird:

Die Formel beschreibt eine der Möglichkeiten, die so genannte »Logistische Gleichung« zu definieren. Sie wurde vom belgischen Mathematiker Pierre-François Verhulst entwickelt, der sich 1838 mit Modellen zum Bevölkerungswachstum beschäftigte. Zuvor hatte der britische Ökonom Thomas Malthus sein berühmtes »Bevölkerungsgesetz« aufgestellt, laut dem die Zahl der Menschen exponentiell wachse, was früher oder später zu einer Katastrophe führen müsse. Verhulst ergänzte jedoch das Modell von Malthus. Er fügte mathematische Terme hinzu, die diverse wachstumshemmende Faktoren beschreiben können.

Im Fall eines Virus wie Covid-19 ist das Wachstum anfangs tatsächlich exponentiell. Es ist aber auch klar, dass es nicht ewig weitergehen kann. Irgendwann fehlen dem Virus die Ressourcen, das heißt: Menschen, die infiziert werden können. Dann steigen die Fallzahlen nur noch linear an, noch später kommt das Wachstum komplett zum Stillstand. Genau das beschreibt die logistische Gleichung. Bezeichnet x die Zeit, dann endet zum Zeitpunkt x₀ das exponentielle Wachstum. L gibt den Maximalwert an, der von der Kurve erreicht werden kann (die Zahl e in der Formel ist die Eulersche Zahl, und k ein Wachstumsfaktor, der angibt, wie steil die Kurve ansteigt).

Darauf zu warten, bis das Virus sich in der Bevölkerung so weit ausgebreitet hat, dass es keine neuen Menschen für eine Infektion mehr findet, wäre allerdings für uns der unangenehmste Ausgang der Pandemie. Deswegen haben auch so viele Länder auf den ersten Blick sehr harte Maßnahmen getroffen, um die Kontakte zwischen Menschen einzuschränken. Ziel ist es, den Wendepunkt x₀ so früh wie möglich zu erreichen, bevor die Zahl der infizierten Menschen das Gesundheitssystem zum kollabieren bringt.

Gerade in einer Situation wie der aktuellen Pandemie ist die Mathematik von besonderem Wert. Sie sagt uns einerseits, womit wir zu rechnen haben, und andererseits, welche Maßnahmen getroffen werden sollten. Sie liefert uns aber auch einen notwendigen emotionsfreien Blick auf die Lage. Wir Menschen sind nicht gut darin, das exponentielle Wachstum intuitiv zu verstehen. Das anfängliche langsame Ansteigen der Fälle kann uns in trügerischer Sicherheit wiegen und uns glauben machen, wir müssten (noch) nichts unternehmen.

Aber wenn erst einmal eine große Anzahl an Menschen infiziert ist, ist es eigentlich schon zu spät. Je früher man entsprechende Maßnahmen trifft, desto eher kann man etwas erreichen. Die Mathematik ist klar. Wir sollten ausnahmsweise wirklich auf sie hören und uns nicht auf unser Bauchgefühl verlassen.