Die fabelhafte Welt der Mathematik: Vergesst den Pi-Tag, feiert lieber den Feigenbaum-Tag

Von der Kreiszahl π, der eulerschen Zahl e oder dem goldenen Schnitt φ haben die meisten Menschen schon gehört. Der Kreiszahl wurde inzwischen sogar ein – zumindest inoffizieller – Feiertag gewidmet: Der 14. März gilt weltweit als »Tag der Mathematik«, da das Datum in US-amerikanischer Schreibweise 3/14 lautet – und damit den ersten Ziffern der berühmten Zahl Pi entspricht. Stattdessen könnte man auch in unserer Datumsnotation die Zahl 14/3 ≈ 4,67… zelebrieren: die Feigenbaum-Konstante!
Die Konstante hat nichts mit Botanik zu tun, falls Sie das befürchten. Sollten Sie noch nie etwas von der Feigenbaum-Konstante δ = 4,669201609102990671853203820466… gehört haben, sind Sie damit nicht allein. Selbst einigen Mathematikerinnen und Mathematikern ist sie höchstwahrscheinlich noch nie begegnet. Dabei ist sie durchaus bedeutsam: Es handelt sich um eine universelle Größe, die im Bereich der dynamischen Systeme immer wieder auftaucht – ganz ähnlich wie Pi in der Geometrie immer wieder anzutreffen ist. Warum sollte man also nicht den Feigenbaum-Tag feiern?
Anders als π wirft δ noch viele Fragen auf: Zum Beispiel ist bis heute unklar, ob sie irrational ist oder irgendwann ein periodisches Verhalten annimmt. Fachleute vermuten sogar, die Feigenbaum-Konstante könnte wie die Kreiszahl transzendent sein. Solche Zahlen sind besonders spannend: Sie gelten als »wirklich zufällige Werte«, weil sie sich nicht als Lösung eines noch so komplizierten Polynoms darstellen lassen. Aber woher kommt die mysteriöse Feigenbaum-Konstante und warum wissen wir so wenig über sie?
Lehren aus der Kaninchenzucht
Alles fing mit Kaninchen an. Im Jahr 1976 veröffentlichte der Physiker Robert May eine Arbeit mit dem einprägsamen Titel »Simple mathematical models with very complicated dynamics«. Darin untersuchte er die zeitliche Entwicklung von Populationen, etwa von Kaninchen: Die Tiere vermehren sich, ihre Zahl steigt, doch gleichzeitig müssen sie um Futter wetteifern und haben Fressfeinde, was die Anzahl der Kaninchen wiederum begrenzt.
May suchte nach einer möglichst einfachen Gleichung, die genau diese Dynamik modellieren könnte. Solche Aufgaben fallen in den Bereich der »Theorie dynamischer Systeme«, die sich mit biologischem Wachstum, Planetenbahnen, Wirtschaftsmodellen oder dem Wetter befassen. Dabei spielen Funktionen f(x), wie sie in der Analysis vorkommen, eine wichtige Rolle. Aber anders als in der Schule untersucht man nicht, wie sich f für verschiedene Zahlenwerte von x verändert. Stattdessen setzt man einen Startwert x0 in die Funktion ein, berechnet das Ergebnis f(x0) = x1 und setzt dieses wieder in die Funktion ein: f(x1) = x2. Das wiederholt man möglichst häufig, um das Verhalten von f zu untersuchen. Konvergieren die Ergebnisse irgendwann gegen einen festen Wert? Schwanken sie periodisch zwischen mehreren Zahlen hin und her? Oder explodieren die Resultate in Richtung unendlich? Selbst einfachste Gleichungen f können je nach Startpunkt x0 ein extrem komplexes Verhalten an den Tag legen, wie der Titel von Mays Arbeit nahelegt.
Doch zurück zu den Kaninchen: Mit welcher Funktion f kann man ihre Population modellieren? Als Startpunkt wählt man die aktuelle Anzahl der Kaninchen k0. Angenommen, innerhalb eines bestimmten Zeitintervalls, zum Beispiel einem Jahr, werden weitere k0 Kaninchenbabys geboren. Die Population wächst also mit einer Rate von r = 2. Damit würde sich die Anzahl der Tiere mit jedem Jahr verdoppeln, bis unser Planet nur noch von Kaninchen bevölkert ist. In Gleichungen ausgedrückt: Nach n Jahren gibt es kn = 2 · kn−1 Kaninchen, also doppelt so viele wie im Vorjahr.
Dabei haben wir allerdings nicht berücksichtigt, dass einige der Tiere sterben – an Altersschwäche, weil sie gefressen werden oder aus welchen Gründen auch immer. Das kann man berücksichtigen, indem man die Wachstumsrate mit einem begrenzenden Faktor der Form (K − kn−1) multipliziert, wobei K die maximale Anzahl an Kaninchen darstellt, die die Population überhaupt erreichen kann. Das Wachstum der Kaninchen folgt demnach der Gleichung: kn = r · kn−1 · (K − kn−1). Aus mathematischer Sicht beschreibt diese Funktion kn(kn−1) eine nach unten geöffnete Parabel. Das heißt: Für kleine Werte von kn−1 wächst die Population im kommenden Jahr an, während sie für große kn−1 schrumpft. Das können wir in der Natur ebenfalls beobachten: Wenn es zu viele Tiere einer Art gibt, sinkt die Population, zum Beispiel weil es nicht genug Futter gibt, anschließend kann sie wieder wachsen.
Die von May beschriebene Formel wird inzwischen als logistische Gleichung bezeichnet. Sie lässt sich vereinfachen, indem man nicht die Gesamtzahl k der Kaninchen untersucht, sondern ihren prozentualen Anteil x = k⁄K in Abhängigkeit vom Maximum K. Damit vereinfacht sich die logistische Gleichung zu: xn = r · xn−1 · (1 − xk−1). Nun kann man für verschiedene Wachstumsraten r untersuchen, wie sich eine Population zeitlich entwickelt, indem man mit einem bestimmten Startwert x0 beginnt und die Ergebnisse wieder und wieder in die Gleichung einsetzt:
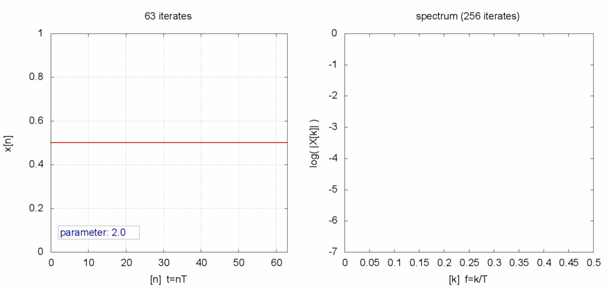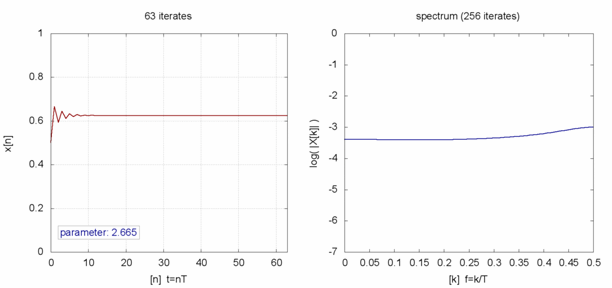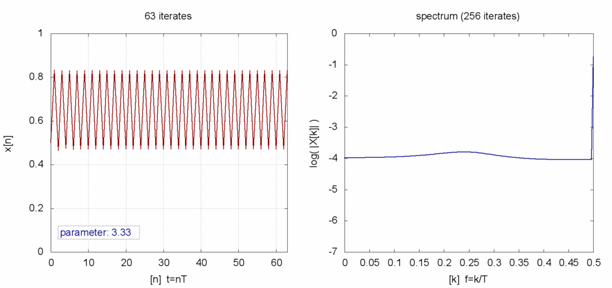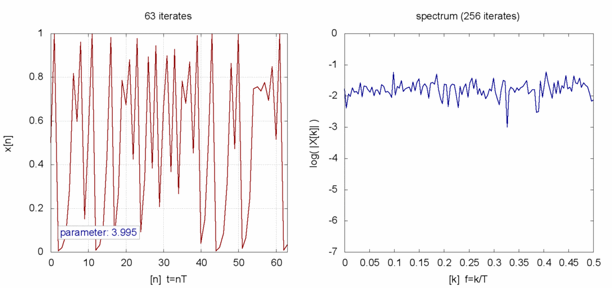
Wie sich herausstellt, hängt das Verhalten der Populationen auf lange Sicht nicht vom Startwert ab – vor allem nicht, wenn man weit in die Zukunft extrapoliert. Die Langzeitergebnisse werden bloß von der Wachstumsrate r beeinflusst. Wenn r zwischen null und eins liegt (also weniger Tiere nachkommen, als bereits vorhanden sind), dann wird die Population nach einer gewissen Zeit zwangsläufig aussterben.
Für r zwischen eins und drei strebt die Anzahl der Tiere nach kurzem Einpendeln gegen einen festen Wert. Auch das spiegelt unsere Erfahrung wider: Viele Populationen haben über Jahre hinweg einen relativ festen Bestand. Wenn man die Wachstumsrate weiter vergrößert, geschieht bei r = 3 erstmals etwas Eigenartiges. Anstatt sich über die vergangene Zeit hinweg einem Zahlenwert zu nähern, springt die Anzahl der Tiere von einem Zeitschritt zum nächsten zwischen zwei festen Punkten hin und her. In einem Jahr könnten 70 Prozent der maximalen Population leben, im nächsten nur 30 Prozent, um dann wieder auf 70 zu steigen. Man spricht von einem dynamischen System mit einer Periodizität von zwei. Auch das kann man im Tierreich beobachten: Manche Populationen haben Zyklen, je nach Jahr oder Jahreszeit sind mal mehr oder mal weniger Tiere anzutreffen.
Wenn die Wachstumsrate weiter anwächst, wird es sogar noch verrückter: Für r zwischen 3,44949 und 3,54409 gibt es vier verschiedene Werte, zwischen denen die Population schwankt, das System hat also eine Periodizität von vier. Mit steigendem r entstehen – in immer kürzeren Intervallen – Bereiche mit Periodizitäten von 8, 16, 32, 64 und so weiter. Die Stelle, an der sich die Periodizität verdoppelt, wird Bifurkation genannt.
Da die Abstände zwischen den Bifurkationen immer kleiner werden, kann man bis r = 3,56995… jede Periodizität in Form einer Zweierpotenz finden – der Größe der Periodizität sind dabei keine Grenzen gesetzt. Darüber hinaus (also für r > 3,56995…) herrscht Chaos. Das bedeutet, dass sich die zeitliche Entwicklung einer Population mit einer solchen Wachstumsrate kaum noch vorhersagen lässt. Zwar kann man für einen festen Wert von r noch immer die Periodizität und die entsprechende Anzahl von Tieren berechnen. Wenn sich r aber nur minimal ändert (was in der Natur durchaus üblich ist), sieht die zeitliche Entwicklung der Population völlig anders aus.
Chaos im Kaninchenbau
Genau das ist die Definition von Chaos. Anders als es der alltägliche Sprachgebrauch nahelegt, bedeutet Chaos im mathematischen Sinn nicht, dass es überhaupt keine Regeln mehr gibt. Rein theoretisch lässt sich ein chaotisches System sogar exakt beschreiben und vorhersagen. Das Problem ist bloß, dass durch winzige Änderungen der Parameter (in diesem Fall die Wachstumsrate r) der Ausgang ein völlig anderer ist. Das macht chaotische Systeme so unberechenbar: Denn man wird nie in der Lage sein, alle relevanten Größen eines komplexen Systems wie etwa des Wetters beliebig exakt zu bestimmen.
Interessanterweise gibt es im chaotischen Bereich von r immer wieder »Inseln der Stabilität«, in denen die Periodizität für längere Intervalle gleich bleibt. Das ist etwa bei r ≈ 3,82843 der Fall. Dort hüpft die Populationszahl zwischen drei Werten hin und her. Kurz darauf folgt ein Bereich, in dem die Zahl zwischen sechs Werten oszilliert, dann ein Intervall mit einer Periodizität von zwölf und so weiter. Auch hier findet man wieder unendlich viele Bifurkationen auf einem kurzen Abschnitt. Tatsächlich kann man im gesamten Bereich von r zwischen null und vier alle möglichen Periodizitäten finden. May hat mit dem Titel seiner 1976 erschienenen Arbeit also voll ins Schwarze getroffen: Wer hätte ahnen sollen, dass eine so einfache Funktion wie r · xn−1 · (1 − xk−1) ein derart komplexes Verhalten an den Tag legt?
Während sich May der logistischen Funktion widmete, arbeitete der Physiker Mitchell J. Feigenbaum ebenfalls an einem chaotischen System, jedoch einem ganz bestimmten: der Turbulenz von Flüssigkeiten. Die so genannten Navier-Stokes-Gleichungen, die das Verhalten von Fluiden beschreiben, sind schon seit dem 19. Jahrhundert bekannt. Dennoch ist man bis heute noch weit davon entfernt, sie lösen zu können – es ist noch nicht einmal bekannt, ob sie immer eine Lösung besitzen. Um sich dem Problem zu nähern, vereinfachte Feigenbaum zunächst die Gleichungen. Er ignorierte ihre räumliche Abhängigkeit, so dass die Formeln bloß noch von der Zeit abhingen. Außerdem betrachtete er die Entwicklung der Gleichungen nur für endliche Zeitschritte. Somit sah auch er sich mit einem dynamischen System konfrontiert, bei dem er den Ausgabewert immer wieder in die ursprüngliche Funktion einsetzen musste – ganz ähnlich wie May.
Viele Systeme verhalten sich auf ähnliche Weise – warum?
Im Juli 1975 besuchte Feigenbaum eine Konferenz zu dynamischen Systemen, an der auch der renommierte Mathematiker Stephen Smale teilnahm. Dieser erzählte Feigenbaum, dass einige Fachleute vermuteten, hinter der Grenze des chaotischen Verhaltens der logistischen Funktion bei r = 3,56995… könnte etwas Tiefgründiges stecken: Vielleicht ließe sich der Zahlenwert 3,56995… durch mathematische Konstanten wie π oder √2 ausdrücken – und vielleicht tauche diese Größe in anderen dynamischen Systemen ebenfalls auf. Feigenbaum war sofort Feuer und Flamme. Zurück in seinem Büro in Los Alamos, stürzte er sich auf seinen Taschenrechner (ein HP-65, der erste programmierbare Taschenrechner) und berechnete die Werte von r, an denen es zu Bifurkationen kommt.
Schnell bemerkte er, dass der Zahlenwert r = 3,56995… an sich nichts Besonderes ist. Doch Feigenbaum fiel eine andere Besonderheit der logistischen Funktion auf. Die Intervalllängen der Periodizitäten werden zwar immer kürzer, aber sie folgen einer gewissen Regel: Das Verhältnis aufeinander folgender Intervalllängen L scheint immer in etwa gleich zu sein. Der Bereich 1 < r < 3 beschreibt zum Beispiel Systeme mit der Periodizität 1, daher ist L1 = 2. Zwischen r = 3 und 3,44949 schwankt die Population hingegen zwischen zwei Werten hin und her (L2 = 0,44949), zwischen r = 3,44949 und 3,54409 hat die Population eine Periodizität von vier (L3 = 0,0946) und so weiter. Nun kann man die Verhältnisse von aufeinander folgenden Intervalllängen L berechnen.
| Intervall | Verhältnis |
|---|---|
| L1/L2 | 4,4495… |
| L2/L3 | 4,7515… |
| L3/L4 | 4,6562… |
| L4/L5 | 4,6683… |
| L5/L6 | 4,6686… |
Mit geeigneten Computerprogrammen lässt sich der Grenzwert der inzwischen als Feigenbaum-Konstante δ bekannten Größe berechnen: δ = 4,669201609102990671853203820466…
Die Feigenbaum-Konstante stößt auf wenig Interesse
Doch Feigenbaum machte noch eine viel erstaunlichere Entdeckung: Die Feigenbaum-Konstante taucht nicht nur im Zusammenhang mit der logistischen Funktion auf, sondern auch mit anderen Funktionen, die ein einziges quadratisches Maximum haben, etwa: xn = r · sin(xn−1). Wenn man die Dynamik solcher Gleichungen für unterschiedliche Parameter r untersucht, findet man die Feigenbaum-Konstante. Denn auch in diesen Systemen verdoppelt sich die Periodizität mit steigender Wachstumsrate. Und wenn man das Verhältnis der jeweiligen Intervalllängen zwischen den Bifurkationen berechnet, kommt wieder die mysteriöse Konstante heraus. Feigenbaum vermutete, dass es sich um eine universelle Größe handelt, die zur Theorie der dynamischen Systeme gehört, so wie Pi zur Geometrie.
Mit dieser Erkenntnis zog der damals 30-Jährige durchs Land und hielt Vorträge. Doch die Begeisterung blieb zunächst aus: Physiker wussten nicht ganz, was sie mit diesem Ergebnis anfangen sollten – hatte es überhaupt eine Relevanz für reale Systeme? Und Mathematiker zeigten sich skeptisch, da Feigenbaum nicht beweisen konnte, dass δ wirklich universell war und nicht nur zufällig in seinen untersuchten Systemen auftauchte. Und so kam es, dass die ersten Versuche, seinen Fund zu veröffentlichen, scheiterten: Zwei mathematische Fachzeitschriften lehnten Feigenbaums Manuskript ab. Im Jahr 1978 schließlich willigte ein physikalisches Fachjournal ein, die erstaunliche Arbeit zu publizieren. Doch erst als ein Forschungsteam um den Experimentalphysiker Albert Libchaber ein Jahr später tatsächlich die Verdopplung der Periodizität in flüssigem Helium beobachten konnte, würdigte die Fachwelt Feigenbaums Erkenntnisse.
Inzwischen gibt es zahlreiche experimentelle Nachweise seiner Arbeit in unterschiedlichsten Bereichen: von Fluiddynamik über optische Systeme bis hin zur Medizin. Unter anderem kann man die dynamischen Modelle nutzen, um Herzrhythmusstörungen zu behandeln, die durch chaotische Erregungsmuster im Herzmuskel entstehen können. Trotz all dieser Erfolge war aber noch immer unklar, wie allgemeingültig Feigenbaums Entdeckung wirklich war. Ohne einen mathematischen Beweis kann man nur Spezialfälle abklappern. Doch glücklicherweise ließ ein solcher nicht allzu lange auf sich warten. 1982 konnte der Mathematiker Oscar Lanford III einen computergestützten Beweis vorlegen, indem er einige Abschätzungen durch aufwändige maschinelle Berechnungen bestätigte. 17 Jahre später gelang es Mikhail Lyubich, einen Beweis ohne Hilfe eines Computers vorzulegen.
Damit ist bewiesen, dass die Feigenbaum-Konstante für die Theorie dynamischer Systeme dieselbe Rolle spielt wie die Kreiszahl Pi für die Geometrie. Es gibt also keinen Grund, am »Tag der Mathematik« nicht auch der Feigenbaum-Konstante zu huldigen – zumal sie besser zu unserer Datumsnotation passt.
Was ist euer Lieblingsmathetheorem? Schreibt es gerne in die Kommentare – und vielleicht ist es schon bald das Thema dieser Kolumne!
Schreiben Sie uns!
3 Beiträge anzeigen