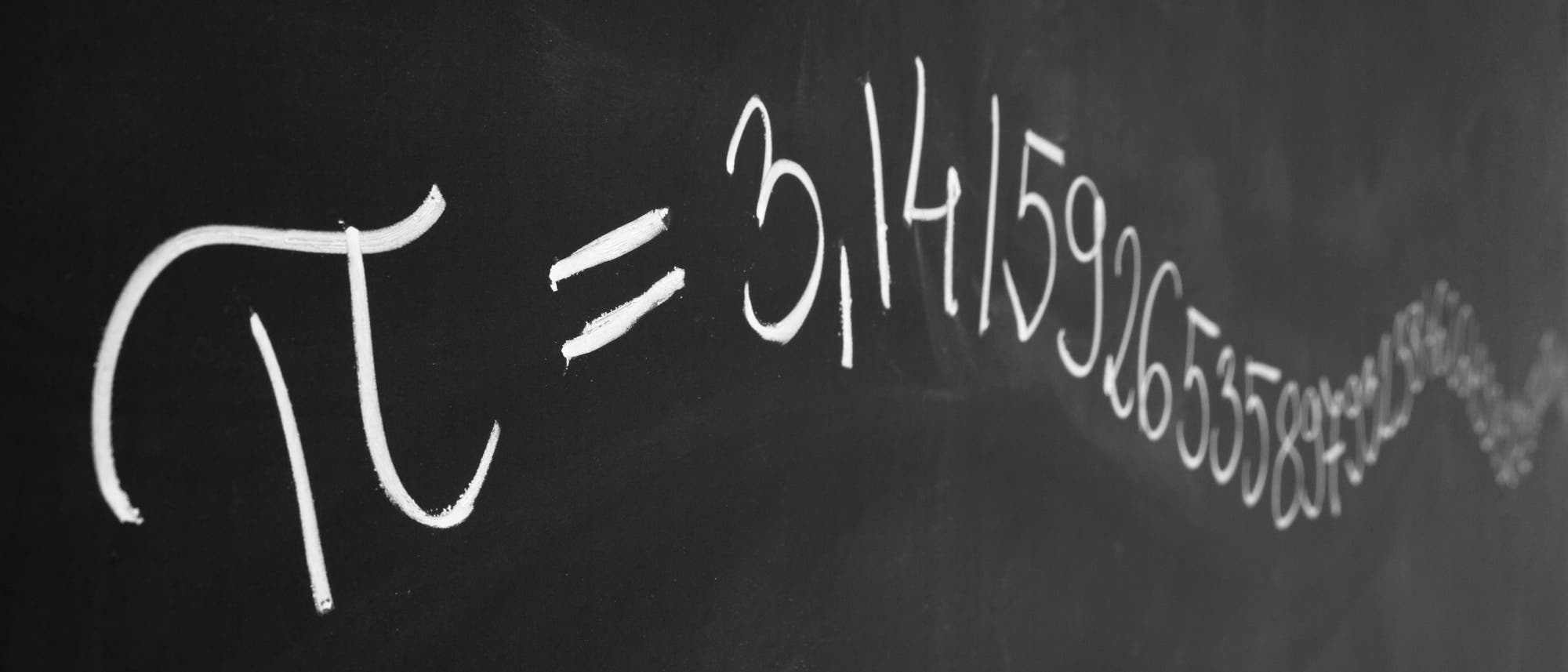
Die natürlichen Zahlen heißen nicht umsonst so; es sind die Zahlen, die wir schon in der Grundschule lernen: 1, 2, 3, 4 und so weiter. Man wird beim Zählen nie an ein Ende kommen. Etwas später lernen wir dann auch andere Zahlen kennen: die ganzen Zahlen, die die natürlichen Zahlen ins Negative erweitern, die Bruchzahlen – die mathematisch korrekt die rationalen Zahlen heißen – und die irrationalen Zahlen, die sich nicht als Bruch darstellen lassen.

Die reellen Zahlen sind die Menge aller rationalen und irrationalen Zahlen. Eine der faszinierenden Erkenntnisse in der Mathematik ist die Feststellung, dass es davon »mehr als unendlich« viele gibt. Etwas korrekter ausgedrückt: Versucht man, jeder reellen Zahl eine natürliche Zahl zuzuordnen, sie also abzuzählen, dann wird man damit scheitern, selbst wenn man berücksichtigt, dass man bis unendlich zählen kann. Es gibt »überabzählbar« viele reelle Zahlen und unterschiedlich »mächtige« Unendlichkeiten.

Das entzieht sich unserer anschaulichen Vorstellung; noch viel überraschender ist aber diese Formel:

Sie beschreibt eine Zahl, die der russische Mathematiker Alexander Jakowlewitsch Chintschin 1935 gefunden hat. Die Formel ist nicht einfach, und man braucht ein paar Informationen, um sie richtig würdigen zu können. Die Sache fängt damit an, dass man eine beliebige reelle Zahl in Form eines Kettenbruchs darstellt – und zwar nach einem ganz spezifischen Rezept.

Die Zahl π etwa hat unendliche viele Stellen hinter dem Komma und beginnt mit 3,1415926… Der ganzzahlige Anteil – vor dem Komma – ist logischerweise 3, und der nicht ganzzahlige Anteil ist ebenso logischerweise π – 3 und muss kleiner als 1 sein. Bilden wir von diesen 0,1415926 den Kehrwert, erhalten wir eine neue Zahl (in diesem Fall 7,0625…). Deren ganzzahligen Anteil können wir ebenfalls abtrennen; so erhalten wir einen weiteren Rest, mit dem wir ebenso verfahren und so weiter. Setzt man all das zusammen, kann man π auch als Abfolge von Brüchen darstellen: π = 3 + (1 / (7 + 1 / (...))).

Die Kettenbruchkonstante

Kettenbrüche verwendet man schon seit Jahrhunderten, etwa, um gute Näherungen für irrationale Zahlen zu finden. Würden wir das Beispiel mit der Zahl π jetzt abbrechen, würden wir eine Näherung von π ~ 3 + (1 / (7 + 1)) = 25/8 = 3,125 erhalten.

Chintschins seltsame Formel beschreibt nun eine höchst überraschende Eigenschaft der Kettenbruchentwicklung reeller Zahlen: Berechnet man das geometrische Mittel all der ganzzahligen Anteile, die im Kettenbruch einer reellen Zahl auftauchen, multipliziert man sie also und bildet aus dem Produkt die n-te Wurzel, wobei n die Anzahl der verwendeten Zahlen ist, dann erhält man im Grenzfall einer unendlich langen Kettenbruchentwicklung als Ergebnis die in der Formel angegebene Zahl K₀.

Das ist höchst erstaunlich! Denn die Formel ist völlig unabhängig von der verwendeten reellen Zahl. Es handelt sich um eine Konstante: K₀ = 2,6854520010… Chintschins Entdeckung gilt nicht für alle reellen Zahlen; die rationalen Zahlen, die naturgemäß eine endliche Kettenbruchentwicklung aufweisen, sind eine offensichtliche Ausnahme. Chintschin konnte jedoch zeigen, dass sein Ergebnis fast überall gilt, wobei »fast überall« hier ein mathematisch exakter Ausdruck ist, der – vereinfacht gesagt – so viel bedeutet wie: Der Bereich, in dem die Aussage nicht gültig ist, spielt keine relevante Rolle im Vergleich zu dem Bereich, wo sie gilt. Wenn Chintschins Konstante für rationale Zahlen nicht anwendbar ist, dann bleiben immer noch überabzählbar viele andere reelle Zahlen, bei denen es funktioniert.

Angesichts der unvorstellbar unendlichen Menge der reellen Zahlen scheint es sehr seltsam, dass man sie alle auf eine Art darstellen kann, die über eine Zahl wie Chintschins Konstante zusammenhängen. Eine Zahl, von der wir noch nicht einmal wissen, ob es eine rationale Zahl ist oder nicht. Aber es ist so, und ob wir das verstehen oder nicht, ist der Mathematik egal.