Was glauben Sie, wie die Folge 1, 2, 4, 8, 16, … weitergeht? Auch ohne viel Ahnung von Mathematik zu haben, würden die meisten wohl auf 32 tippen – schließlich haben sich alle zuvor aufgelisteten Werte verdoppelt. Allerdings nimmt die Folge, die sich der Zahlentheoretiker Leo Moser (1921–1970) im Jahr 1949 ausgedacht hat, eine überraschende Wendung: Auf die 16 folgt die 31. Tatsächlich lauten die ersten Glieder der in der Online-Enzyklopädie der Zahlenfolgen als »A000127« bezeichneten Sequenz: 1, 2, 4, 8, 16, 31, 57, 99, 163, 256, 386, … Auch wenn sie also ganz unschuldig mit Zweierpotenzen beginnt, weicht sie ab dem sechsten Glied plötzlich davon ab. Moser nutzte dieses Beispiel, um davor zu warnen, vorschnelle Schlüsse aus vermeintlichen Mustern abzuleiten.

Nun gut, irgendeine wirre Zahlenfolge kann sich jeder ausdenken. Allerdings hat die Moser-Folge, auch Mosersches Kreisflächenproblem genannt, nicht umsonst einen Eintrag in der berühmten Zahlenfolgen-Enzyklopädie OEIS: Die Zahlen folgen tatsächlich einem Muster – allerdings einem etwas komplizierteren, als dem von bloßen Zweierpotenzen. Sie lässt sich an einem anschaulichen Beispiel exemplarisch herleiten: dem Zerteilen einer Pizza.

Angenommen, zwei Personen wollen eine Pizza in viele kleine Stücke schneiden. Die eine Person markiert dafür Punkte am Teigrand, die andere macht dann einen Schnitt zwischen allen eingezeichneten Punkten. Dafür fährt sie mit einem Pizzaschneider von je einem Punkt aus zu jedem anderen am Rand. Die Frage, die Moser sich stellte, war: Wie viele Pizzastücke können dabei maximal entstehen?

Seltsame Pizza-Muster

Bei nur einem Punkt kann man die Pizza nach den genannten Regeln nicht teilen, es gibt also nur ein Stück. Bei zwei Punkten lässt sich die Fläche, wenn man die Punkte verbindet, in zwei schneiden. Bei drei Punkten kann man drei Schnitte vornehmen, wodurch die Fläche gevierteilt wird. Bei vier Punkten sind es sechs Schnitte und es ergeben sich acht Pizzastücke und so weiter. Wie sich herausstellt, verdoppelt sich anfangs die Anzahl der entstehenden Stücke pro hinzukommendem Punkt. Doch sobald man sechs Punkte vorgesetzt bekommt, bricht das Muster zusammen, die Pizza besteht dann aus 31 Stücken. Aber warum?

Um das zu verstehen, braucht man eine Formel, die angibt, wie viele Flächen für n Randpunkte entstehen. Das direkt zu ermitteln, ist gar nicht so leicht. Deshalb starten wir mit einem einfacheren Zusammenhang und zählen zunächst die Schnitte, die sich durch n Punkte ergeben, wenn man sie alle mit einem Pizzaschneider miteinander verbindet. Das heißt, eigentlich suchen wir die Anzahl aller Punktepaare. Wer im Kombinatorik-Unterricht in der Schule aufgepasst hat, weiß, dass es dafür eine griffige Größe gibt, den Binomialkoeffizienten B: B(n,2) = n!/(2!(n−2)!). Das lässt sich am Beispiel mit n = 5 Randpunkten schnell überprüfen, in diesem Fall gibt es B(5,2) = 10 Schnitte.

Ähnlich kann man vorgehen, um herauszufinden, wie oft sich die Schnittkanten kreuzen. Eine einfache Überlegung liefert diese Lösung: Betrachtet man die Pizza mit einem, zwei oder drei Punkten am Rand, kreuzen sich die Schnitte nicht (außer an den Randpunkten natürlich). Ab vier Schnitten gibt es hingegen einen Schnittpunkt in der Mitte, an dem sich zwei der Schnittkanten in die Quere kommen. Pro vier Punkte hat man also einen Schnittpunkt. Damit lässt sich deren Anzahl wieder durch einen Binomialkoeffizienten ausdrücken: B(n,4), bei n am Rand verzeichneten Punkten. Für das Beispiel mit n = 5 Randpunkten ergibt das B(5,4) = 5 Schnittpunkte auf der Pizza.

Doch was, wenn sich mehr als zwei Schnittkanten in einem Punkt kreuzen? Solche Fälle lassen wir außer Acht, denn die Anfangsfrage von Moser lautete, wie viele Pizzastücke sich maximal ergeben. Um die Anzahl der Flächen möglichst groß zu halten, muss man Schnittpunkte von mehr als zwei Kanten vermeiden. Das gelingt, indem man die am Rand markierten Punkte leicht verschiebt.

Damit kennen wir also die Anzahl der Schnitte und der Schnittpunkte. Wenn man die zerteilte Pizza genauer betrachtet, erinnert sie an einen Graphen: Sie besteht aus einem Wirrwarr aus Punkten, die durch Schnitte miteinander verbunden sind. Deshalb kann man den eulerschen Polyedersatz verwenden, den ich in einer vorangangenen Kolumne erklärt habe: Demnach gibt es in jedem Graph, bei dem alle Punkte miteinander verbunden sind, einen Zusammenhang zwischen der Anzahl aller Punkte V, Kanten E und Flächen F: V − E + F = 1.

Von Pizzastücken zur Graphentheorie

Dieser Zusammenhang gilt immer. Wenn wir also wissen, wie viele Punkte und Kanten es in einem Graph gibt, lässt sich daraus die Anzahl der Pizzastücke berechnen. Das einzige Problem: In unserem Beispiel entspricht die Anzahl der Schnitte nicht den Kanten in der Formel, denn jeder unterbrochene Schnitt zählt als eigenständige Kante des Graphen.

Um die Anzahl aller Kanten zu bestimmen, hilft es, sie in verschiedene Kategorien einzuteilen. Zunächst gibt es jene, die zwei Punkte am Rand verbinden, ohne von anderen Schnitten unterbrochen zu werden. Wie man schnell feststellt, sind das die Schnitte, die entlang des Rands verlaufen und jeweils benachbarte Punkte verbinden. Von diesem Kanten-Typ gibt es bei n Randpunkten ebenfalls n Stück. Das kann man am Beispiel von n = 5 schnell sehen.

Dann gibt es die zweite Kategorie von Kanten, die innere Schnittpunkte mit Randpunkten verbinden. Jeder der B(n,2) getätigten Schnitte ist durch jeweils zwei Randpunkte begrenzt. Das heißt, von allen Randpunkten gehen insgesamt 2·B(n,2) Kanten aus. Allerdings sind dabei auch die Kanten vom ersten Typ inbegriffen, also solche, die zwei Randpunkte miteinander verbinden. Diese muss man natürlich von der Rechnung abziehen, um sie am Ende nicht doppelt zu zählen. Damit gibt es also 2·(B(n,2)−n) Kanten vom zweiten Typ, die äußere Randpunkte mit inneren Schnittpunkten verbinden. Für n = 5 Randpunkte ergibt das 2·(10−5) = 10.

Schließlich gibt es noch einen dritten Kantentyp: solche, die innere Schnittpunkte untereinander verbinden. An jedem inneren Schnittpunkt (von denen es B(n,4) gibt) enden vier Kanten. Demnach ist jeder innere Schnittpunkt mit vier Kanten verbunden, was insgesamt 4·B(n,4) Kanten ergibt. Damit hat man die wahre Anzahl aber stark überschätzt: Denn es wurden alle Kanten mitgezählt, die innere Punkte und Randpunkte verbinden. Die muss man abziehen: 4·B(n,4) − 2·(B(n,2)−n). Danach hat man immer noch zu viele Kanten: Wenn zwei innere Schnittpunkte zusammenhängen, hat man deren Verbindung doppelt gezählt. Also muss man ihre Anzahl halbieren: ½ · 4·B(n,4) − 2·(B(n,2)−n) = 2·B(n,4) − (B(n,2)−n). Und wieder kann man das Ergebnis für n = 5 Punkte testen: 2·5 − (10−5) = 5 Kanten, die innere Punkte miteinander verbinden.

Nun muss man nur noch alle drei Kantentypen zusammenzählen, um ihre Gesamtzahl zu erhalten: n + 2·(B(n,2)−n) + 2·B(n,4) − (B(n,2)−n) = 2·B(n,4) + B(n,2). Damit ist man fast bereit, die Anzahl der Pizzastücke zu berechnen. Es fehlt nur eine Kleinigkeit: Da wir die Pizza zu einem Graphen abstrahiert haben, um die eulersche Formel verwenden zu können, stellt der Rand der Pizza auch Kanten dar. Deshalb kommt zu der zuvor berechneten Gesamtzahl noch der Summand n hinzu. Damit hat man das E aus der eulerschen Formel bestimmt: E = 2·B(n,4) + B(n,2) + n. Und auch V kennen wir bereits, die Anzahl der Schnittpunkte plus die n Randpunkte, also: V = B(n,4) + n.

Die Binomialkoeffizienten sorgen für Überraschungen

Aus der eulerschen Formel erhält man folgende Formel für die Anzahl der Pizzastücke: F = 1 − V + E = 1 − B(n,4) − n + 2·B(n,4) + B(n,2) + n = 1 + B(n,4) + B(n,2). Wenn man also eine Pizza vor sich hat, n Punkte markiert und sie durch B(n,2) Schnitte teilt, erhält man 1 + B(n,4) + B(n,2) Pizzastücke. Und wie sich herausstellt, ergibt das für n = 1, 2, …, 5 immer die Zweierpotenz 2ⁿ⁻¹ – und weicht ab n = 6 davon ab. Grund dafür sind die Binomialkoeffizienten, die in der Formel auftauchen.

Vielleicht erinnern Sie sich an den Ursprung der Binomialkoeffizienten, die binomischen Formeln: (a + b)ⁿ. Der binomische Lehrsatz besagt, dass die ausmultiplizierten Terme folgende Form haben: (a + b)ⁿ = B(n,0)·aⁿ + B(n,1)·aⁿ⁻¹b + B(n,2)·aⁿ⁻²b² + … + B(n,n−1)·abⁿ⁻¹ + B(n,n)·bⁿ, wobei B(n,0) = B(n,n) = 1. Wenn man statt abstrakten Variablen a und b für beide den Wert 1 einsetzt, erhält man eine Summe für die Zweierpotenz: 2ⁿ = B(n,0) + B(n,1) + B(n,2) + … + B(n,n−1) + B(n,n) = 1 + B(n,1) + B(n,2) + … + B(n,n−1) + 1. Listet man die Binomialkoeffizienten untereinander für verschiedene Werte von n auf, ergibt sich die folgende extrem symmetrische Struktur:

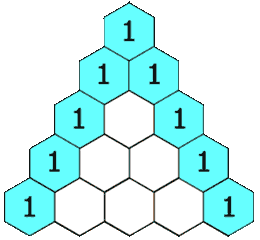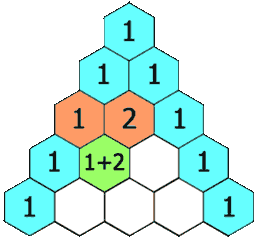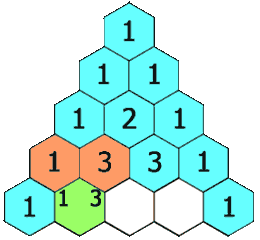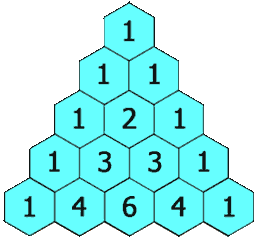
Die Summe aus zwei benachbarten Koeffizienten einer Reihe ergibt immer den Wert in der darunter befindlichen Reihe. Das kann man ausnutzen, um die Formel für die Pizzastücke (1 + B(n,2) + B(n,4)) zu vereinfachen. Geht man in der Tabelle der Binomialkoeffizienten eine Reihe weiter nach oben (also in die n−1-te Reihe), kann man ausnutzen, dass: B(n,2) = B(n−1,1) + B(n−1,2) und B(n,4) = B(n−1,3) + B(n−1,4). Damit erhält man eine neue Formel für die Anzahl der Pizzastücke (die selbstverständlich genau dieselben Ergebnisse liefert): 1 + B(n,2) + B(n,4) = 1 + B(n−1,1) + B(n−1,2) + B(n−1,3) + B(n−1,4). Das Ergebnis entspricht den ersten vier Summanden zum Berechnen der Zweierpotenz 2ⁿ⁻¹. Falls n also kleiner ist als sechs, stimmt die Anzahl der Pizzastücke mit der Summenformel für die Zweierpotenz überein. Sobald man aber einen weiteren Punkt hinzufügt, bricht die Summe frühzeitig ab und das Ergebnis weicht von der Zweierpotenz ab.

Damit wissen Sie nun, wie Sie eine Pizza problemlos in 31 Stücke aufteilen können – auch wenn nicht alle Portionen gleich groß ausfallen werden. Zum Glück sind große Partypizzen meist rechteckig, da kommt es zu weniger Überraschungen.

​​Was ist euer Lieblingsmathetheorem? Schreibt es gerne in die Kommentare – und vielleicht ist es schon bald das Thema dieser Kolumne!