Die fabelhafte Welt der Mathematik: Pi ist überall – Folge 2
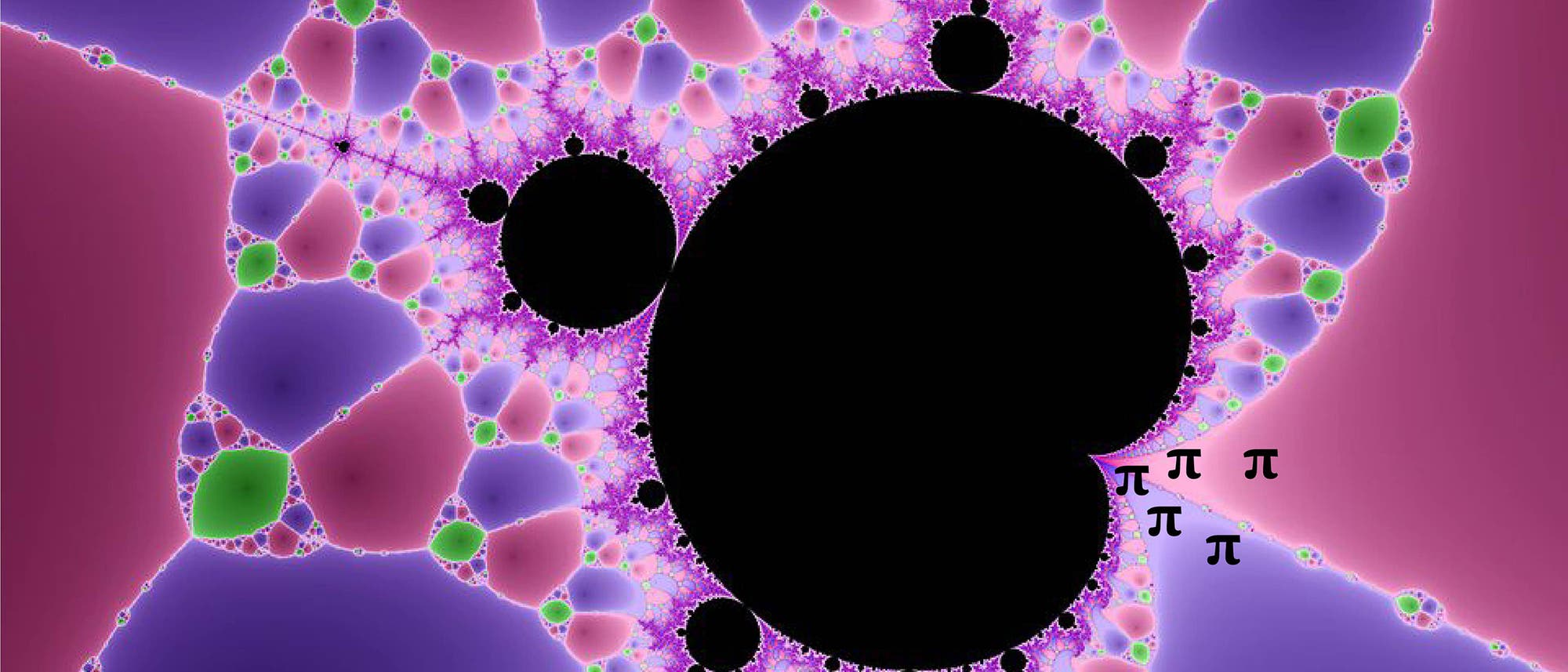
Die Mandelbrotmenge ist das wohl berühmteste Fraktal der Mathematik. Wie passend, dass sich ausgerechnet die bekannteste irrationale Zahl des Fachs darin versteckt! Das zu erkennen, ist allerdings gar nicht so einfach. Die Mathematikerin Holly Krieger von der University of Cambridge bezeichnete die Mandelbrotmenge als die »vielleicht ineffizienteste Art und Weise, Pi zu berechnen«.
Das Apfelmännchen besticht durch seine Ästhetik: Wie bei allen Fraktalen kann man in einen Ausschnitt hineinzoomen, wobei sich unter verbesserter Auflösung die gleichen Muster offenbaren wie zuvor. Die Details nehmen kein Ende, man kann die Teile beliebig weiter vergrößern und findet stets dieselben Strukturen vor. Seit Jahrhunderten faszinieren Fraktale daher nicht nur die Fachwelt, sondern auch Menschen, die mit Mathe eigentlich wenig anfangen können.
Ein unendliches Muster
Doch wie kommt die Mandelbrotmenge überhaupt zu Stande? Formal ist sie über eine rekursive Gleichung definiert. Dabei handelt es sich um eine Funktion, die man für einen gewissen Startwert berechnet und deren Ergebnis man dann wieder in die Formel einsetzt – und dieser Vorgang wird immer wieder wiederholt. Für die Mandelbrotmenge lautet die Gleichung folgendermaßen: zn+1 = zn2 + c, mit dem Startwert z0 = 0. Wenn c also etwa den Wert 2 hat, dann ist z0 = 0 (wie in der Definition vorgegeben), z1 = z20 + 2 = 2, z2 = z21 + 2 = 6 und so weiter. Wie man leicht sieht, entsteht eine Folge, die schnell immer weiter anwächst.
Wählt man hingegen einen kleinen c-Wert wie ¼, sind die Werte der rekursiven Gleichung beschränkt: z0 = 0, z1 = ¼, z2 = 1⁄16 + ¼ = 5⁄16, z3 = 25⁄256 + ¼, … Die Werte zn werden dabei niemals ½ überschreiten. Ebenso kann man negative Zahlen für c einsetzen, wodurch ebenfalls beschränkte Folgen entstehen, das heißt, die Werte steigen niemals ins Unermessliche – unabhängig davon, wie häufig man sie wieder in die Funktion einsetzt. Das führt zur Definition der Mandelbrotmenge: Sie enthält alle Punkte c, die zu beschränkten Folgen führen. Demnach ist c = ¼ sowie c = –¾ in der Menge enthalten, aber c = 2 nicht.
Ausflug in die komplexe Zahlenebene
Die Mandelbrotmenge wäre jedoch ziemlich langweilig, wenn man sich auf die reellen Zahlen beschränken würde, denn dann bestünde sie bloß aus einer Linie. Mathematiker berücksichtigen daher auch imaginäre Zahlen, die Wurzeln aus negativen Zahlen. Wenn man diese quadriert, ergibt sich ein negativer Wert – was bei der Funktionsvorschrift für die Mandelbrotmenge spannende Ergebnisse bietet. Um die Punkte c der Menge abzubilden, nutzt man für gewöhnlich die so genannte komplexe Zahlenebene: Die x-Achse besteht dabei wie gewohnt aus reellen Zahlen, die y-Achse stellt aber imaginäre Werte dar. Dadurch entspricht ein Punkt (2, 5) im Koordinatensystem einer komplexen Zahl z = 2 + 5i, wobei i die Wurzel aus minus eins ist.
In der komplexen Ebene nimmt die Mandelbrotmenge ihre vollständige fraktale Form an. Sie markiert alle komplexen Zahlen c, für welche die rekursive Formel zn+1 = zn2 + c beschränkt bleibt.
Wenn man sich die Figur genau ansieht, kann man erkennen, dass an der Stelle (−¾, 0) ein einzelner Punkt zu sein scheint, der zwei Bereiche der Mandelbrotmenge scharf voneinander trennt. Das wollte der Informatikstudent Dave Boll im Jahr 1991 genauer untersuchen. Dafür betrachtete er winzige Abweichungen von dieser Stelle (etwa den Punkt (–¾, 0,001)) und berechnete, wie viele Wiederholungen n man braucht, bis der Wert von zn zwei übersteigt. (Man wählt häufig die – willkürlich festgelegte – Zahl 2, weil die rekursive Gleichung beim Erreichen dieses Werts ganz sicher nicht mehr beschränkt ist.) Als Boll verschiedene Abweichungen der Größe 0,1; 0,01; 0,001 und so weiter von dem Punkt (–¾, 0) untersuchte, erlebte er eine Überraschung:
| Abweichung | Iteration |
|---|---|
| 1 | 3 |
| 0,1 | 33 |
| 0,01 | 315 |
| 0,001 | 3143 |
| 0,0001 | 31417 |
| 0,00001 | 314160 |
| 0,000001 | 3141593 |
| 0,0000001 | 31415928 |
Je näher der Wert an den interessanten Punkt rückt, desto mehr Nachkommastellen von Pi entfalten sich in n. Damit hatte Boll nicht gerechnet – ebenso wenig wie die Mathematikerinnen und Mathematiker, die er damit konfrontierte. Doch bevor er mit einem Erklärungsversuch aufwartete, sah er sich zunächst einen anderen Punkt der Mandelbrotmenge an: den »Hintern« des Apfelmännchens mit den Koordinaten (¼, 0). Er wollte herausfinden, ob Pi auch dort auftaucht. Als er die gleiche Analyse an der neuen Stelle durchführte, erhielt er folgende Zahlenreihe:
| Abweichung | Iteration |
|---|---|
| 1 | 2 |
| 0,01 | 30 |
| 0,0001 | 312 |
| 0,000001 | 3140 |
| 0,00000001 | 31414 |
| 0,0000000001 | 314157 |
Wo kommt Pi her?
Wieder schien die Folge gegen die Nachkommastellen von Pi zu streben – wenn auch langsamer als zuvor. Wie sich herausstellte, gibt es weitere Punkte in der Mandelbrotmenge, an denen man Pi auf ähnliche Weise konstruieren kann. Um herauszufinden, wo die Kreiszahl herkommt, muss man die Werte der iterativen Gleichung, der das fraktale Muster zu Grunde liegt, untersuchen. Denn in ihnen versteckt sich eine trigonometrische Funktion, die π an diesen völlig unerwarteten Stellen erzeugt.
Wir hatten bereits gesehen, dass die iterative Funktion für c = ¼ (also der Hintern des Apfelmännchens) niemals Werte annimmt, die größer sind als ½. Die Zahlen nähern sich zwar immer weiter ½ an, je häufiger man sie in die Gleichung einsetzt, doch ohne den Wert jemals zu erreichen. Setzt man nun statt ¼ c = 0,26 in die iterative Gleichung ein, erhält man folgende (gerundete) Zahlenfolge: 0,26; 0,328; 0,367; 0,395; 0,416; 0,433; 0,448; 0,46; 0,472; 0,483, 0,493; 0,503; 0,513; 0,523; 0,534; 0,545; 0,557; 0,57; 0,585; 0,602; 0,623; 0,648; 0,68; 0,722; 0,781; 0,87; 1,017; 1,294; 1,934; 3,999; 16,251; … Anfangs wachsen die Werte nur sehr langsam an, bis sie schließlich explosionsartig ansteigen.
Wie sich herausstellt, ist das für alle Werte c so, wenn sie nahe bei ¼ liegen. Je kleiner die Abweichungen vom Hintern des Apfelmännchens sind, desto langsamer wachsen die Werte der Folge an. Man kann beobachten, dass es sehr lange dauert, bis sie ungefähr die Zahl ½ erreichen – danach aber rapide größer werden.
Um also herauszufinden, wie Pi in die ganze Sache verwickelt ist, muss man verstehen, wie viele Wiederholungen n nötig sind, bis zn den Wert ½ annimmt. Das heißt, man sucht die Zahl n, für die zn = ½. Da es kompliziert ist, eine iterative Gleichung auf diese Art zu untersuchen, nimmt man eine gewöhnliche Funktion f(n) zur Hilfe: f(n) = zn – ½. Die Nullstellen n der Funktion entsprechen dann genau den Werten n, die wir suchen.
Perspektivwechsel: Von einer Folge zu Funktionswerten
Im Klartext bedeutet das: Anstatt die Werte zn der iterativen Gleichung als Zahlenfolgen anzusehen, betrachten wir sie nun als Ergebnis einer gewöhnlichen Funktion f(n). Wenn man diese kennt, braucht man nur noch ihre Nullstellen zu berechnen, um hoffentlich auf die Zahl Pi zu stoßen.
Mathematikerinnen und Mathematiker haben das für Punkte in der Nähe des Hinterns des Apfelmännchens gemacht, also für Koordinaten der Form (¼ + ε, 0), wobei ε der Abweichung (0,1; 0,001; 0,0001 und so weiter) entspricht. Wie die Fachleute herausfanden, ist die Funktion, welche die Zahlenfolge erzeugt, näherungsweise: f(n) = √ε · tan(√ε · n). Diese Funktion ist immer dann null, wenn √ε · n die Zahl Pi ergibt. Das heißt, n entspricht – zumindest in guter Näherung – einem Vielfachen von zehn von Pi. Damit entfalten sich nach und nach die unendlich vielen Nachkommastellen der Kreiszahl.
Doch wie Holly Krieger bereits festgestellt hat: Wenn man auf diese Weise Pi möglichst exakt bestimmen möchte, ist man lange beschäftigt. In der Mathematik geht es aber glücklicherweise nicht nur um Effizienz. Manchmal genügt es, dass ein Ergebnis vollkommen unerwartet ist, damit es Berühmtheit erlangt.
Was ist euer Lieblingsmathetheorem? Schreibt es gerne in die Kommentare – und vielleicht ist es schon bald das Thema dieser Kolumne!
Schreiben Sie uns!
3 Beiträge anzeigen