Es handelt sich um eine spezielle mathematische Methode, die in der Allgemeinen Relativitätstheorie (ART) mit Erfolg eingesetzt wird. Diese Technik wurde von Arnowitt, Deser und Misner 1962 entwickelt und ist außerordentlich nützlich für die Numerische Relativitätstheorie.

Motivation zu dieser Methode

Wenn man physikalische, dynamische Prozesse in einer gekrümmten Raumzeit untersuchen möchte, ergibt sich das Problem, dass die Zeit in jedem Punkt der vierdimensionalen Mannigfaltigkeit anders ablaufen kann: hier schneller, da langsamer, sie kann sogar – für einen Außenbeobachter – stillstehen! Dies ist besonders problematisch, wenn man zeitabhängige Prozesse simulieren möchte, weil man nicht weiß, welcher Beobachter (FIDO, FFO, ZAMO) der geeignete ist und eine 'richtige Physik' beschreibt. Generell erlaubt die ART von einem auf den anderen Beobachter zu transformieren. Dies geschieht mittels Lorentz-Transformationen und Poincaré-Transformationen.

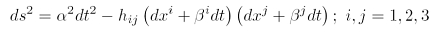
Und so geht's

Im ADM-Formalismus spaltet man nun die von der Relativitätstheorie geschaffene Symmetrie zwischen Raum und Zeit (daher Raumzeit) wieder auf. Deshalb nennt man diese Methode auch den 3+1 Split, weil man in die drei Raumkoordinaten einerseits und die eine Zeitkoordinate andererseits aufspaltet. Dies gelingt dadurch, dass man die vierdimensionale Raumzeit aus dreidimensionalen raumartigen Hyperflächen zusammensetzt, auf denen der Zeitparameter jeweils konstant ist. Der Ablauf der Zeit geschieht nun durch 'Springen' von einer Hyperfläche zur nächsten in dieser Foliation (Blätterung) aus Hyperflächen. Jede Hyperfläche hat ihre eigene Drei-Metrik, h_ij, die man aus der kovarianten, vierdimensionalen (also übergeordneten) Metrik gewinnt: es sind gerade die Elemente der unteren, rechten 3 × 3-Matrix, die in die 4 × 4-Matrix des so dargestellten metrischen Tensors (in einem bestimmten Koordinatensystem) eingebettet sind. Die Gleichung oben zeigt das Linienelement der ART, das die Eigenschaften einer Raumzeit charakterisiert. Hier steht es bereits in 3+1 Form: der linke Term enthält die Zeitdimension, der rechte die drei Raumdimensionen. Jede (nicht pathologische) Raumzeit kann in diese Form gebracht werden, so dass man die Größen α und β identifizieren kann. Aber was sagen uns nun diese Größen?

Wer α sagt, muss auch β sagen

Von einer Hyperfläche zur nächsten vermittelt die Lapse-Funktion (übliche Bezeichnung mit α) die Veränderung des Zeitablaufs. Physikalisch betrachtet ist die Lapse-Funktion gerade das Differential der Eigenzeit über dem der Beobachterzeit, also die Gravitationsrotverschiebung. Die Lapse-Funktion misst gerade diejenige Zeit, die für den lokalen Beobachter – FIDO genannt – vergangen ist, wenn für den unendlich entfernten Außenbeobachter gerade eine Einheit seiner 'universellen' Zeit vergangen ist.
Auf einer Hyperfläche selbst vermittelt der Shift-Vektor (β) eine Verschiebung im 3D-Raum innerhalb einer Hyperfläche. Es handelt sich um eine Verschiebung des räumlichen Koordinatengitters gegenüber dem des FIDOs. Der Begriff Shift-Vektor geht auf den Relativisten John A. Wheeler zurück (1964). Im Frame-Dragging-Effekt der Kerr-Metrik wird diese Verschiebung anschaulich klar. Das 3D-Koordinatengitter in Boyer-Lindquist-Koordinaten wandert im 3+1 Split der Kerr-Geometrie entlang der azimutalen Richtung: der Raum selbst wird um die Rotationsachse des sich drehenden Schwarzen Loches gedreht.

Vorteil: Studie dynamischer Prozesse in der ART

Lapse, Shift und 3-Metrik sind alle zeitunabhängig und legen dann eindeutig eine neue Formulierung der Metrik im 3+1 Split fest! Auf diese Art und Weise hat man sich eine globale Zeit konstruiert, kann zeitabhängige Prozesse allgemein relativistisch beschreiben und numerisch studieren. Entsprechend kann man bei der Untersuchung magnetohydrodynamischer Prozesse einen 3+1 Split des Maxwell-Tensors vornehmen, der dabei in elektrisches und magnetisches Feld zerfällt. Aber auch in der allgemein relativistischen Hydrodynamik muss der 3+1 Split verwendet werden.

Eine Verallgemeinerung des soeben beschriebenen In-Scheiben-Schneidens der Raumzeit, des ADM-Slicings, gelingt in der Loop-Quantengravitation, einer Quantengravitation, die ihre fundamentalen Quanten in Loops bzw. in neuerer Formulierung in Spin-Netzwerken sieht. Ihre Zeitentwicklung bildet den Spinschaum auf der Planck-Skala. Slicing des Spinschaums liefert gerade Momentaufnahmen von Spin-Netzwerken.