Das Äquivalenzprinzip ist das wichtigste Prinzip, auf dem Albert Einsteins Allgemeine Relativitätstheorie (ART) beruht. Andere wichtige Prinzipien der ART sind das Machsche Prinzip, das Kovarianzprinzip, das Korrespondenzprinzip und das Prinzip minimaler gravitativer Kopplung.

Kernaussage dieses Prinzips

In seiner knappen Formulierung besagt das Äquivalenzprinzip:

Schwere Masse und träge Masse sind gleichwertig.

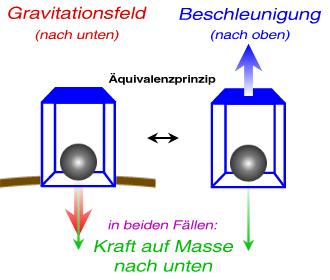Das bedeutet, dass es für einen Beobachter in einem abgeschlossenen Kasten nicht möglich ist zu unterscheiden, ob der Kasten auf der Oberfläche einer Masse in dessen Gravitationsfeld steht oder ob er gleichmäßig durch eine konstant wirkende Kraft ohne Gravitationsfeld im freien Raum beschleunigt wird. Diese beiden Fälle werden in der Abbildung rechts veranschaulicht: Wie man sieht, wirkt die Beschleunigung durch die Gravitation links genau entgegengesetzt zur Beschleunigung rechts; Testmassen innerhalb des Kastens – hier eine Kugel – zeigen dennoch in beiden Fällen das gleiche Verhalten und werden durch die gleiche Kraft (grüner Pfeil) nach unten gezogen.
Eine etwas andere Formulierung des Äquivalenzprinzips ist, dass man durch lokale Experimente nicht entscheiden kann, ob sich ein System im freien Fall in einer gekrümmten Raumzeit befindet oder ob es kräftefrei eine gleichförmig geradlinige Bewegung in flacher Raumzeit ausführt. Beide Systeme führen zu äquivalenten Beobachtungsphänomenen. Diese Eigenschaft heißt lokale Lorentzinvarianz: Man kann in der ART immer ein lokales Lorentzsystem konstruieren.
Bisweilen unterscheidet man die schwere Masse in passive schwere Masse, wenn ein Körper passiv in einem Gravitationsfeld fällt und in aktive schwere Masse, wenn ein Körper aktiv ein Gravitationsfeld erzeugt.

Historische Wegbereiter des Einsteinschen Äquivalenzprinzips

Galilei

Die berühmten Fall-Experimente Galileo Galileis (1564 – 1642) am Schiefen Turm von Pisa belegten, dass verschiedene Körper im freien Fall die gleiche Beschleunigung erfahren, also zum gleichen Zeitpunkt am Boden ankommen, unabhängig von ihrer Masse und Zusammensetzung. Diese Beobachtung Galileis wird als schwaches Äquivalenzprinzip bezeichnet. Gegensätzliche Beobachtungen sind meist die Folge des Luftwiderstandes und können in evakuierten Fallanordnungen eliminiert werden.

Eötvös

Im Jahr 1891 entwarf der ungarische Naturwissenschaftler Loránd Eötvös (1848 – 1919) – der übrigens auch in Heidelberg studierte – das erste Drehwaagen-Experiment. Mit dieser Anordnung konnte er die Gravitationskonstante G mit einer erstaunlichen Genauigkeit ermitteln. Das Messprinzip beruht darauf, dass zwei Massen unterschiedlicher Dichte starr miteinander durch einen Stab bekannter Länge verbunden sind und dieses hantelförmige Gebilde an einem Draht aufgehängt wird. Durch die Wirkung äußerer Gravitationskräfte werden die Massen aufgrund verschiedener Dichten unterschiedlich stark ausgelenkt: der Draht wird durch ein Drehmoment verdrillt (Torsion). Rückstellkräfte im Draht versuchen nun diesem Einfluss entgegenzuwirken, und es entsteht eine Torsionsschwingung. Die Methode ist dynamisch, weil sich die Massen zwischen massiven Wänden bewegen.
Mit diesem experimentellen Aufbau kann der Experimentator entweder bei sehr exakt bekannten Massen die Gravitationskonstante ermitteln, was von Interesse für die Physik ist, oder er kann unter Zugrundelegung der Gravitationskonstante das irdische Gravitationsfeld vermessen, was Eötvös im Dienste der Geologie anwandte.

Hochpräzision in experimenteller Physik

Die Drehwaagen erlaubten schon damals im 19. Jahrhundert, die Äquivalenz von schwerer und träger Masse bis auf eine Genauigkeit von 1:10⁸ genau zu ermitteln. Mittlerweile wurde das Experiment mittels Laser verfeinert (EötWash-Experiment) und die Genauigkeit gehört zu den präzisesten Messungen der Physik: träge und schwere Masse sind bis auf 1:10¹³ genau gleich!

Ein Pendel genauer betrachtet

Die Äquivalenz von schwerer und träger Masse setzt man übrigens stillschweigend beim Lösen der Pendelgleichung in der Mechanik voraus. Denn hier kürzt man die Masse des Schwingers heraus: auf der einen Seite der Gleichung seine schwere Masse, auf der anderen Seite seine träge Masse. Umgekehrt kann man gerade aus exakten Messungen in solchen Pendelexperimenten auf die Äquivalenz der Massen schließen.

Bedeutung des Äquivalenzprinzips

Die Unabhängigkeit von der Masse beim Fall von Testkörpern im Gravitationsfeld ist bereits ein Hinweis darauf, dass Gravitation eine geometrische Eigenschaft ist. Denn gemäß der ART ist Gravitation eine gekrümmte Raumzeit, in der sich Licht und Materieteilchen auf Geodäten bewegen!
Einstein nutzte das Äquivalenzprinzip aus, um seine Spezielle Relativitätstheorie auf beschleunigte Bezugssysteme zu verallgemeinern. Am Ende dieser Jahre dauernden, theoretischen Ausarbeitungen stand die Allgemeine Relativitätstheorie, eine (unquantisierte) Gravitationstheorie, die sehr erfolgreich unzählige Phänomene, die mit der Gravitation zusammenhängen, beschreibt.
Das Äquivalenzprinzip führt auch zu der Äquivalenz von Hawking-Effekt (im Gravitationsfeld Schwarzer Löcher) und Unruh-Effekt (im Vakuum).