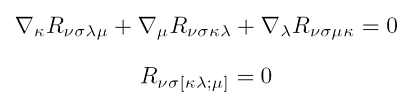
Die Tensoren der Allgemeinen Relativitätstheorie (ART) haben wie viele physikalische Tensoren bestimmte Symmetrieeigenschaften. Mit Symmetrie meint man in diesem Zusammenhang, dass eine oder mehrere Komponenten im Tensor als andere Komponenten identisch wieder auftauchen. Diese Eigenschaften sind sehr nützlich, weil man im Tensorkalkül der ART immer an sämtlichen Komponenten der Tensoren interessiert ist, um beispielsweise die Einsteinschen Feldgleichungen umzuformulieren. Bekannte Symmetrien erleichtern den Rechenaufwand, weil man aus ihnen schnell andere Komponenten ableiten kann. Typisch ist bei Tensoren zweiter Stufe, dass sie sich nicht verändern, wenn man ihre beiden Indizes vertauscht. In der Darstellung als Matrix wird klar, dass dies eine Vertauschung von Spalten und Zeilen ist. Die Symmetrie ist dann eine Spiegelsymmetrie zur Matrixdiagonalen.

Formen von Bianchi-Identitäten

• algebraische Identitäten: Hier zeigen sich Symmetrien von Tensoren, wenn man ihre Indizes vertauscht und Summen oder Differenzen bildet.
• differentielle Identitäten: Hierbei sind die Verknüpfungsrelationen komplizierter und enthalten Ableitungen (Differentiationen).

Eine besondere Symmetrieeigenschaft von Raumzeiten bewerkstelligen die Isometrien. Man kann durchaus die Killing-Gleichung, also verschwindende Lie-Ableitung des metrischen Tensors, als differentielle Identität auffassen.
Die Bianchi-Identitäten sind nun ebenfalls differentielle Identitäten, die für den Riemann-TensorR gelten. Die Ableitungen, die hier eine Rolle spielen, sind die kovarianten Ableitungen, die man mit dem Differentialoperator Nabla (als Symbol ein auf einer Ecke stehendes, gleichseitiges Dreieck: ∇) notiert. Der Krümmungstensor ist im Prinzip die linke Seite der Einsteinschen Feldgleichungen und von zentraler Bedeutung für die ART. Der Riemann-Tensor ist ein Tensor 4. Stufe und kann durch einmaliges 'Überschieben' des metrischen Tensors (Verjüngen oder Kontrahieren genannt) in den Ricci-Tensor und durch zweimaliges Verjüngen in den Ricci-Skalar (skalare Krümmung) überführt werden. Wendet man dies unter Kenntnis der Bianchi-Identitäten an, so erhält man die kontrahierten Bianchi-Identitäten. Weil der Einstein-Tensor eng mit dem Riemann-Tensor und dessen Kontraktionen zusammenhängt, gelingt eine äußerst kompakte Notation, die vier Gleichungen mit je vier Termen bündelt. Diese vier Gleichungen nennt man auch differentielle Bindungen.

Geometrische Interpretation der Energieerhaltung in der Physik!

Die Bianchi-Identitäten sind jedoch weit mehr als eine Rechenhilfe. Sie sind Ausfluss eines tiefsinnigen, geometrischen Sachverhalts, den der französische Mathematiker Elie Joseph Cartan (1869 – 1951) folgendermaßen formulierte: 'Der Rand eines Randes ist null.' Dieses elementare Prinzip der Topologie sorgt dafür, dass der Einstein-Tensor divergenzfrei ist, wie es die kontrahierten Bianchi-Identitäten wiedergeben. Die Folge dieser Eigenschaft ist für die Physik von essentieller Bedeutung: sie mündet in den relativistischen Energieerhaltungssatz: die Divergenzfreiheit des Energie-Impuls-Tensors. Das führt auf zwei wichtige Prinzipien, die die Physik in vielfältiger Weise beherrschen: Energieerhaltung und Impulserhaltung. Prosaisch umschrieben sind die Quellen (des Gravitationsfeldes) automatisch erhalten. In der Differentialgeometrie kann man zeigen, dass jede glatte Riemannsche Mannigfaltigkeit die Bianchi-Identitäten erfüllt. Damit hat die Energieerhaltung als physikalisches Prinzip eine geometrische Erklärung erfahren!
Historisch war es so, dass Albert Einstein bei der Entwicklung seiner ART die Arbeiten des italienischen Mathematikers Luigi Bianchi (1856 -1928) zu den Nicht-Euklidischen Geometrien nutzte. Die nach ihm benannten Bianchi-Identitäten fanden Gregorio Ricci-Curbastro (1853 – 1925) 1889 und er selbst 1902 unabhängig voneinander. Der deutsche Mathematiker Hermann Klaus Hugo Weyl (1885 – 1955) konnte die Identitäten 1917 aus Emmy Noethers Theorem abgeleiten. Das Noether-Theorem stellt einen Zusammenhang zwischen einer Symmetrie und assoziierter Erhaltungsgröße her.

Buchtipp

• Eine sehr empfehlenswerte Darstellung zum letztgenannten Aspekt, Energieerhaltung und Geometrie, befindet sich in Misner, Thorne & Wheeler: Gravitation, Kapitel 15