Die Cauchy-Fläche oder Cauchy-Horizont ist eine besondere Fläche, die im Verständnis Schwarzer Löcher eine Rolle spielt. Man definiert sie wie folgt: Eine Cauchy-Fläche ist eine Hyperfläche einer Raumzeit, die eine kausale Kurve exakt nur einmal schneiden kann.

Bitte im Klartext!

Dies bedarf sicher einiger Erklärungen: Eine Raumzeit ist eine vierdimensionale Mannigfaltigkeit, die eine Lösung der Einsteinschen Feldgleichungen der Allgemeinen Relativitätstheorie (ART) ist. Eine Hyperfläche zu diesem 4D-Gebilde ist deshalb dreidimensional. Im ADM-Formalismus wird die Raumzeit beispielsweise in Hyperflächen zerlegt, um numerische Relativitätstheorie betreiben zu können (3+1 Split). Mit der oben genannten kausalen Kurve meint man eine Weltlinie, also eine Kurve in der Raumzeit, die beispielsweise ein Beobachter oder ein Materieteilchen zurücklegt. Kausale Kurven sind aber nicht in die Vergangenheit fortzusetzen! Die Bedingung des 'Einmalschneidens' bedeutet also anschaulich, dass Cauchy-Flächen nur in einer Richtung durchlässig sind.

Mehr Horizonte beim Loch

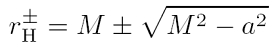Der Bezug zu Schwarzen Löchern ist der Folgende: Betrachtet man die Kerr-Lösung, die die rotierende Raumzeit Schwarzer Löcher beschreibt, so findet man beim Nullsetzen des Delta-Potentials in Boyer-Lindquist-Koordinaten im Allgemeinen zwei Lösungen dieser quadratischen Gleichung: Die eine bezeichnet man mit r₊ und kann gerade mit dem Ereignishorizont, dem äußeren Horizont Schwarzer Löcher, identifiziert werden. Die andere Lösung, r₊, ist der innere Horizont und besagte Cauchy-Fläche.

Seltsame Effekte am Cauchy-Horizont

Gelangt nun ein Beobachter auf einer Geodäte hinter den Cauchy-Horizont, so wird er Zeuge, wie die gesamte Geschichte der Außenwelt in Zeitraffer abläuft. Denn er erreicht eine Region unendlicher Blauverschiebung. Dummerweise wird er dann auch von einem energetisch betrachtet unendlichen Strahlungsblitz getroffen.
Eine seltsame Eigenschaft von Cauchy-Horizonten ist, dass sie singulär werden, wenn sie durch Objekte, die sie passieren, gestört werden. Cauchy-Horizonte sind singuläre Nullhyperflächen. Diese seltsamen Eigenschaften deuten darauf hin, dass hier die Domäne einer Quantengravitation beginnt.

Literatur:

• Chandrasekhar, S.: The Mathematical Theory of Black Holes (1983), S.214
• Townsend, P.K.: Black Holes (1997), Preprint: gr-qc/9707012