Rotation ist eine wichtige Eigenschaft von Himmelskörpern. Spiralgalaxien rotieren, Sterne rotieren, Planeten rotieren um ihr Zentralgestirn, so auch die Erde um die Sonne, sogar Schwarze Löcher rotieren (Kerr-Lösung).

Drehimpuls in der klassischen Mechanik

Physikalisch ausgedrückt hat ein Körper, der rotiert, Drehimpuls. Allgemein berechnet man den Drehimpuls J in der klassischen Mechanik (unquantisiert, unrelativistisch) mittels des Vektorprodukts aus dem radialen Abstand r des Teilchens zum Drehzentrum mit dem Impuls des rotierenden Teilchens p: J = r × p = r ×mv. Im letzten Schritt wurde ausgenutzt, dass der Impuls eines Teilchens das Produkt aus Masse m und Geschwindigkeit v ist.

Rotationsformen

Vergleicht man nun das Rotationsverhalten von Probeteilchen um ein Drehzentrum, so lässt sich unterschiedliches Rotationsverhalten charakterisieren (siehe Abbildung). Zu Beginn, also vor der Rotation, mögen Testteilchen auf einer Linie liegen. Dann setzen zwei unterschiedliche Rotationstypen ein (links gegenüber rechts unten).

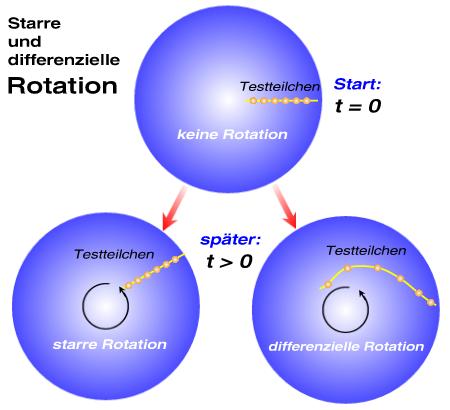
Eine differenzielle Rotation ist zu unterscheiden von der starren Rotation. Bei der starren Rotation rotieren Punkte (Testteilchen in der Abb.) mit verschiedenem Abstand zum Drehzentrum mit gleicher Winkelgeschwindigkeit, also auf einer immer gleich bleibenden Verbindungslinie (mathematisch: die radiale Ableitung der Winkelgeschwindigkeit ist konstant). Das ist in der Abbildung links unten dargestellt. Die Winkelgeschwindigkeit entspricht übrigens dem Quotienten aus Umlaufgeschwindigkeit und Radius der Bahn. Winkel- und Umlaufgeschwindigkeit sind nicht dasselbe!
Bei der differenziellen Rotation rotieren Punkte verschiedenen Abstands mit unterschiedlicher Winkelgeschwindigkeit (die radiale Ableitung der Winkelgeschwindigkeit ist abhängig vom Abstand, Radius). Das ist in der Abbildung rechts unten zu sehen. Verständlich wird der Unterschied im Rotationsverhalten anhand von Beispielen: Eine starre Rotation erfüllen alle starren Festkörper (daher der Name), weil sie nicht deformierbar sind, z.B. ein Karussell. Eine differenzielle Rotation ist in einer Kepler-Scheibe, also beispielsweise bei den Planeten im Sonnensystem gegeben. Die Winkelgeschwindigkeit von Merkur ist höher, als die der Erde.

Bezug zu Akkretion und MHD

Differenzielle Rotation ist eine wesentliche Voraussetzung, damit die magnetische Rotationsinstabilität (MRI) funktioniert. Die MRI ist ein wichtiger Mechanismus, der in der Magnetohydrodynamik von Akkretionsflüssen auftritt.