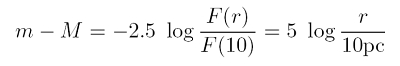
Eine wichtige Relation in der Astronomie, die die Entfernung eines leuchtenden Objekts, beispielsweise eines Sterns, in Bezug setzt zu dessen Helligkeit (dort finden sich weitere Details zum Entfernungsmodul).
Bei ermittelter Distanz r aus Entfernungsbestimmungsmethoden, folgt die absolute Helligkeit M daher direkt aus bekannter (weil beobachteter) scheinbarer Helligkeit m.

wichtige Anwendung: Entfernungsbestimmung

Oder umgekehrt, wie es bei Cepheiden, RR Lyrae Sternen, Supernovae Typ Ia oder anderen Standardkerzen gemacht wird: aus beobachteter, scheinbarer Helligkeit m und aus theoretischen Sternmodellen fixierten absoluten Helligkeiten M folgt die Entfernung! Diese letzte Anwendung ist besonders wichtig in der Vermessung des Universums, der Kosmometrie. Die Kenntnis der Entfernung kosmischer Quellen ist für die Astronomen von großem Wert, weil andere physikalische Größen häufig von der Entfernung abhängen.

Beispiel: Sonne

Wer einmal mit der Gleichung 'spielen' mag, sei dazu eingeladen, die scheinbare visuelle Helligkeit der Sonne, m_V = -26.7^mag, und ihre absolute visuelle Helligkeit, M_V = 4.87^mag, einzusetzen, um den Abstand der Sonne zur Erde zu berechnen. Und siehe da: das Ergebnis sind gerade etwa 150 Millionen Kilometer oder eine Astronomische Einheit.

Kosmologie

Bei sehr großen Entfernungen muss das oben formulierte Distanzmodul mit den Methoden der relativistischen Kosmologie verallgemeinert werden. Zusätzlich gehen dann in die Formel die kosmologischen Parameter ein, die das jeweilige Friedmann-Weltmodell festlegen. Ein gut geeigneter Entfernungsbegriff ist dann die so genannte Leuchtkraftdistanz.