Der Doppler-Effekt gehört zu den wichtigsten Phänomenen in der Physik. Es handelt sich um einen Effekt, der mathematisch beschreibt, wie sich die Wellenlänge eine Welle verändert, wenn sich der Wellenerreger oder der Wellenempfänger bewegen. Vertraut ist uns dieser Effekt im Alltag, wenn sich die Tonhöhe einer relativ zu uns bewegten Schallquelle verändert, z.B. das Martinshorn eines Rettungswagens oder das Motorengeräusch in der Formel-1. Der Doppler-Effekt tritt allerdings nicht nur bei akustischen Wellen auf, sondern vor allem auch bei elektromagnetischen Wellen – das macht ihn bedeutsam für die Astronomie.

Namenspate

Der Doppler-Effekt wurde nach dem österreichischen Physiker und Mathematiker Christian Johann Doppler (1803 – 1853) benannt. Er veröffentlichte 1842 bei der Böhmischen Gesellschaft der Wissenschaften in Prag das Papier Über das farbige Licht der Doppelsterne und einiger Gestirne des Himmels. Darin modellierte Doppler das Licht fälschlicherweise als longitudinale Welle – bereits 1821 hatte A.J. Fresnel (1788 – 1827) behauptet, dass Licht eine transversale Welle sei. Wie wir heute wissen, hatte Fresnel Recht, doch die wesentliche Aussage von Dopplers Arbeit bleibt bestehen. Doppler machte darüber hinaus den bemerkenswerten und weitsichtigen Kommentar, dass Astronomen den von ihm entdeckten Effekt benutzen werden, um die Bewegung und Entfernung der Sterne zu messen – er sollte Recht behalten.

akustischer Doppler-Effekt

Schallwellen breiten sich in einem Medium, z.B. Luft oder Wasser, mit der Schallgeschwindigkeit aus. Die empfangene Frequenz erhöht sich bzw. die empfangene Wellenlänge verkürzt sich, wenn sich die Schallquelle auf den Empfänger zu bewegt. Die sich ausbreitende Welle wird anschaulich gewissermaßen gestaucht. Entfernt sich die Schallquelle, passiert das genaue Gegenteil, denn die empfangene Frequenz wird niedriger bzw. die empfangene Wellenlänge wird erhöht. Dann wird die sich fortpflanzende Welle anschaulich gesprochen gedehnt.

Doppler-Effekt bei Licht

Bei dem Doppler-Effekt von elektromagnetischer Strahlung verhält es sich ein bisschen anders: Licht benötigt kein Medium um sich auszubreiten und kann sich sogar im Vakuum fortpflanzen. Aus diesem Grund empfangen Astronomen überhaupt elektromagnetische Signale kosmischer Quellen. Albert Einstein hat bei der Begründung seiner Spezielle Relativitätstheorie 1905 gefordert, dass Licht sich immer gleich schnell ausbreitet – unabhängig von dem Bewegungszustand der Lichtquelle! Diese experimentell verifizierte Forderung heißt Postulat von der Konstanz der Vakuumlichtgeschwindigkeit c. Es hat gravierende Konsequenzen für unser Verständnis von Raum und Zeit. Offensichtlich ist der Doppler-Effekt von Licht völlig anders, als derjenige akustischer Wellen, deren Fortpflanzungsgeschwindigkeit ja variieren kann.
Phänomenologisch bleibt das oben Gesagte erhalten: Die empfangene Lichtfrequenz ν_obs erhöht sich bzw. die empfangene Wellenlänge verkürzt sich, wenn sich die Lichtquelle mit der Relativgeschwindigkeit v auf den Beobachter zu bewegt. Weil dies einer Veränderung der Lichtfarbe mit der emittierten Frequenz ν_em zum Blauen hin entspricht, nennen Physiker diesen Effekt Blauverschiebung.
Entfernt sich die Lichtquelle, wird die empfangene Strahlungsfrequenz kleiner bzw. die empfangene Lichtwellenlänge wird größer. Die Physiker sprechen dann von einer Rotverschiebung, genauer einer Doppler-Rotverschiebung. Quantitativ berechnet man das mit den Gleichungen für den speziell relativistischen Doppler-Effekt:

Der Doppler-Faktor

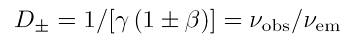Physiker schreiben diese Gleichungen gerne noch kompakter und benutzen dazu den Lorentz-Faktor γ ist und die in der Relativitätstheorie übliche auf die Vakuumlichtgeschwindigkeit normierte Geschwindigkeit β = v/c. Umschreiben und zusammenfassen der beiden Gleichungen oben führt zur Gleichung links. Hierin ist D der Doppler-Faktor. Das Pluszeichen gilt für eine Doppler-Rotverschiebung und das Minuszeichen für eine Doppler-Blauverschiebung.
Der Doppler-Faktor kann in der Allgemeinen Relativitätstheorie (ART) verallgemeinert werden und heißt dann oft nicht mehr D, sondern g-Faktor g, Rotverschiebungsfaktor oder relativistisch verallgemeinerter Doppler-Faktor (siehe auch A. Müller: The Onset of General Relativity: gravitationally redshifted emission lines, Astron. Nachr. 327, 1024, 2006; ePrint: astro-ph/0610791).
Der Doppler-Faktor bzw. g-Faktor ist von grundlegender Bedeutung in der Strahlungsphysik, weil er einerseits das Maß dafür ist, wie die Strahlungsenergie vom Ruhesystem ins Beobachtersystem verschoben wird und weil er andererseits in hoher Potenz den Strahlungsfluss, also die gemessene Intensität der Doppler-verschobenen Strahlung, beeinflusst. Generell ist das Verhältnis aus spektraler Strahlungsintensität I_ν und dritter Potenz der Frequenz ν – beide betrachtet im gleichenBezugssystem – eine Invariante. Daraus folgt die sehr nützliche Gleichung rechts, um vom Ruhesystem auf das Beobachtersystem zu transformieren.

Vorsicht: drei Arten der Rotverschiebung!

Die Rotverschiebung involviert eine Reihe von Missverständnissen. Die oben erläuterte Doppler-Rotverschiebung darf auf gar keinen Fall mit der kosmologischen Rotverschiebung verwechselt werden! Hintergrund ist, dass die Rotverschiebung als Verschiebung im Spektrum ganz unterschiedliche physikalische Ursachen haben kann. Bei der Doppler-Rotverschiebung ist die Ursache eine Bewegung, genauer gesagt eine Relativbewegung, die zu einer Entfernung zwischen Emitter und Beobachter führt. Es gibt aber noch zwei weitere Formen der Rotverschiebung, die nur mit Einsteins ART zu verstehen sind. Da ist zunächst die kosmologische Rotverschiebung. Sie beruht darauf, dass sich eine Raumzeit ausdehnt. Genau das geschieht mit unserem Universum: der ganze Raum (präzise: die Raumzeit) expandiert, so dass auch die darin enthaltenen Lichtwellen auseinander gezogen werden. Das geschieht beispielsweise mit der kosmischen Hintergrundstrahlung seitdem sie sich in der Rekombinationsepoche (vor gut 13 Mrd. Jahren) ausbreitet. Entsprechend entfernen sich auch die Galaxien voneinander, weil sich das Universum immer mehr vergrößert – das geschieht sogar beschleunigt, weil die Dunkle Energie den Kosmos auseinander treibt.
Es wäre nun völlig falsch die kosmologischen Rotverschiebungen zu benutzen, um kosmische Fluchtgeschwindigkeiten von weit entfernten Galaxien auszurechnen. Dass das keinen Sinn macht, erkennt man schnell daran, dass für weit entfernte Systeme diese Fluchtgeschwindigkeit die nach Einstein nicht überschreitbare Vakuumlichtgeschwindigkeit übersteigt. Solche Rechnungen machen keinen Sinn, zumal ein Geschwindigkeitsbegriff für ein sich ausdehnendes Raumzeitgitter von zweifelhaftem Wert wäre.
Die letzte Form der Rotverschiebung ist die Gravitationsrotverschiebung. Sie ist auch nur mit Einsteins ART zu verstehen. Licht verliert nämlich Energie, wenn es in einem Gravitationsfeld ausbreitet. In der Sprache Einsteins ist Schwerkraft eine gekrümmte Raumzeit und Licht folgt hier ausgezeichneten Bahnen, den so genannten Nullgeodäten. Anschaulich argumentiert kämpfen die Lichtwellen wie eine startende Rakete mit der Gravitation und verlieren Energie. Während einer Rakete der Treibstoff ausgeht, bedeutet Energieverlust für Photonen eine Verschiebung zum Roten hin. In diesem Fall spricht der Physiker von einer Gravitationsrotverschiebung, weil die Ursache der Rotverschiebung die Gravitation ist. Extrem wird dieser Effekt bei einem Schwarzes Loch: am Ereignishorizont haben die Lichtwellen all ihre Energie und Intensität an die Gravitation verloren. Das verleiht dem Loch die charakteristische Schwärze.
Im Allgemeinen ist eine beobachtete Rotverschiebung die Summe aus diesen drei Rotverschiebungen, also Doppler-Rotverschiebung, Gravitationsrotverschiebung und kosmologische Rotverschiebung. Das erschwert natürlich die Arbeit des Astronomen, und er benötigt weitere Informationen über den Emitter, um die Gewichtung der Rotverschiebungen herauszufinden.

Beispiele aus der Astronomie

• Mit der Doppler-Whobbling-Methode bestimmen Planetenjäger die Relativgeschwindigkeiten von Sternen entlang der Sichtlinie (so genannte Radialgeschwindigkeit) und können aus dem Hin- und Herpendeln eines Sterns indirekt auf einen extrasolarenPlaneten schließen – ohne ihn direkt zu beobachten! Über die Kepler-Gesetze gelingt sogar eine Massenbestimmung des Planeten (bei bekannten Sternparametern).
• Die Geschwindigkeiten eines Sternenwinds bestimmen die Astronomen bequem mit der Doppler-Blauverschiebung.
• Die Wellenlängen der Spektrallinien verschiedener Elemente und Moleküle kennen die Astronomen aus Untersuchungen im Labor. Sie kennen also die Wellenlängen der Übergänge im Ruhesystem. Beobachten sie nun die gleiche spektrale Signatur bei einer kosmischen Quelle, so folgen bei Kenntnis der zugrunde liegenden Physik, die Eigenschaften des Emitters, z.B. sein Bewegungszustand, das Temperaturmilieu (Doppler-Verbreiterung) oder – bei hohen Entfernung – die kosmologische Rotverschiebung. Bei relativistisch verbreiterten Eisenlinien, die in der Nähe Schwarzer Löcher ausgesandt werden, können alle drei Rotverschiebungen relevant sein.
• Das historische Paradebeispiel ist die Entdeckungsgeschichte der Quasare: Das Spektrum dieser Form leuchtkräftiger Aktiver Galaktischer Kerne wurde erst verstanden, als der Astronom Maarten Schmidt die Emissionslinien als hohe kosmologische Rotverschiebungen (nicht Doppler-Rotverschiebung!) deutete. Das entlarvte die Quasare als extrem weit entfernte, extragalaktische Objekte des jungen Universums.
• Die Jets von kompakten Objekten bewegen sich in der Regel mit relativistischen Geschwindigkeiten. Die Strahlung der Jets wird somit vom speziell relativistischen Doppler-Effekt beeinflusst. Ein extremes Beispiel sind die Jets der Blazare, die auf den Beobachter zeigen und stark blauverschoben sind.

Faustformel für blauverschobene, relativistische Jets

Für das letztgenannte Beispiel benutzen Astronomen eine knappe Schreibweise, in die der Jet unter beliebigen Winkeln orientiert sein kann. Der relativistische Jet möge mit einem Neigungswinkel i (Inklination) auf den Beobachter zeigen. Dieser Winkel sei so definiert, dass i=0° bedeute, dass der Jetstrahl genau auf den Beobachter zeige und i=90°, dass der Jetstrahl senkrecht zur Sichtrichtung sei (keine Geschwindigkeitskomponente in Richtung Beobachter). Der Doppler-Faktor D für Blauverschiebung der Jetemission berechnet sich dann gemäß der Gleichung rechts. Anschaulich projiziert der Kosinus den Jetgeschwindigkeitsvektor auf die Blickrichtung.

longitudinaler und transversaler Doppler-Effekt

Anhand der letzten Gleichung ist ein interessantes Phänomen zu zeigen: Selbst wenn der Jet nicht auf den Beobachter zeigt (i=90°) gibt es einen Doppler-Effekt! Denn der erste Term in der Klammer ('1') bleibt bestehen. Es bleibt eine Abhängigkeit vom Lorentz-Faktor, der wiederum eine Funktion des Geschwindigkeitsfelds des Jets ist. Die Bewegungen im Jet tragen immer noch zu einem Doppler-Effekt bei, obwohl relativ zum Beobachter gar keine Relativgeschwindigkeit vorliegt! Dieser resultierende Doppler-Effekt für diesen Spezialfall heißt transversaler, speziell relativistischer Doppler-Effekt, weil der Doppler-Effekt hier senkrecht (d.h. transversal) zur Blickrichtung auftritt. Dieser Beitrag wird nur bei relativistischen Geschwindigkeiten bedeutsam – bei kleinen Geschwindigkeiten gegenüber der Vakuumlichtgeschwindigkeit wird γ ~ 1 und somit D ~ 1 und schließlich ν_obs ~ ν_em. Dieser Ausdruck kann für die ART verallgemeinert werden. Dann skaliert der Doppler-Faktor mit der Lapse-Funktion.
Demgegenüber wird der Doppler-Effekt mit Geschwindigkeitskomponente des Emitters in Blickrichtung longitudinaler Doppler-Effekt genannt.

Literaturquelle

• Website: MacTutor History of Mathematics archive, University of St. Andrews, Scotland; darin die Biographie von C.J. Doppler