Lexikon der Astronomie: Eddington-Leuchtkraft
Eddington-Leuchtkraft und Eddington-Akkretionsrate sind bedeutende Größen in der Akkretionsphysik. Sie dienen dazu, um das Vermögen einer Quelle einzuschätzen, um Materie aufzusammeln und die bei der Akkretion freiwerdende Gravitationsenergie in Form elektromagnetischer Wellen abzustrahlen. Insoweit benötigen Astrophysiker die Eddington-Grenze, um die Strahlungsleistung und das Akkretionsverhalten von Aktiven Galaktischen Kernen (AGN) wie die Quasare und Seyfertgalaxien einerseits, aber auch den Röntgendoppelsternen und Protosternen andererseits beurteilen zu können. Mit der Eddington-Relation kann auch die Masse des Materie aufsammelnden Objekts, des so genannten Akkretors, abgeschätzt werden.
Eddington-Limit: Strahlung kann den Einfall stoppen
Bei der Ableitung dieser charakteristischen Größe der Akkretionsphysik beginnt man bei der Eddington-Leuchtkraft. Die Eddington-Leuchtkraft ist diejenige Leuchtkraft, bei der der nach außen gerichtet Strahlungsdruck auf ein Volumenelement im Akkretionsfluss gerade so groß wird wie der nach innen gerichtete Gravitationsdruck. Mit anderen Worten: Eine Quelle mit einer Leuchtkraft oberhalb des Eddington-Limits bläst die Materie in der Umgebung mit der Strahlung weg und bremst oder unterbindet gar die Akkretion. Wenn der Grenzfall gerade erfüllt ist, sprechen die Astronomen von einer Quelle am Eddington-Limit. Ist die Leuchtkraft sogar noch größer, so sprechen sie von einer super-Eddington-Quelle. Entsprechend gibt es auch die sub-Eddington-Quellen, bei denen die Leuchtkraft unter der Eddington-Grenze liegt.
Und so wird's berechnet
Eine Berechnung aus dem Druckgleichgewicht von Strahlungs- und Gravitationsdruck führt auf die Gleichung für die Eddington-Leuchtkraft:
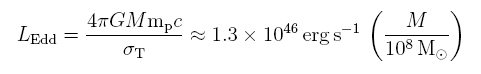
Hier sind G = 6.672 × 10-8 cm3 g-1 s-2 die Gravitationskonstante, M die Masse des Akkretors, z.B. eines Schwarzen Lochs oder eines Neutronensterns, mp = 1.6726231 × 10-24 g bezeichnet die Protonenmasse, weil vor allem diese schweren Teilchen den Gravitationsdruck in einem Volumenelement des Stroms ausmachen, c = 29979245800 cm s-1 ist die Vakuumlichtgeschwindigkeit, σT ist der Wirkungsquerschnitt der Thomson-Streuung (Zahlenwert: 6.6524 × 10-25 cm2), da der Strahlungsdruck auf das Volumenelement besonders durch Streuung der Photonen an den Elektronen hervorgerufen wird. Dabei ist erg eine sehr gebräuchliche Einheit im cgs-System für die Energie. Astrophysiker bevorzugen die Verwendung von erg gegenüber Joule.
physikalische Bedeutung
Diese erste Gleichung lädt zur Diskussion ein: Sie besagt, dass – wie man intuitiv erwarten würde – ein Akkretor größerer Masse eine größere Leuchtkraft erzeugt. Das ist plausibel, hat doch eine schwere Masse ein tieferes Gravitationspotential als eine leichte Masse. Akkretion ist nicht anderes als das Umwandeln von Gravitationsenergie in Strahlungsenergie. Plakativ gesagt, leuchtet ein akkretierender AGN heller als ein Neutronenstern. Das deckt sich auch glücklicherweise mit den astronomischen Beobachtungen.
Effizienz und Eddington-Akkretionsrate
Die Leuchtkraft mit der Dimension Energie/Zeit kann über eine Größe namens Effizienz (in folgender Gleichung ε) an eine Akkretionsrate mit der Dimension, Masse pro Zeit, koppeln. Die Effizienz macht eine Aussage darüber, wie effizient die akkretierte Masse in Strahlung umgewandelt werden kann. Ein typischer, empirischer Wert für die Effizienz ist 10% (bei schnell rotierenden Löchern kann er auch bei 42% liegen!). Korrigiert man um einen Faktor c2 wird aus der Masse eine Energie und aus der Leuchtkraft eine Akkretionsrate: Aus der Eddington-Leuchtkraft wird so die Eddington-Akkretionsrate:
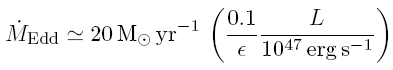
Die zweite Gleichung sagt aus, dass der leuchtkräftigere von zwei Quasaren auch eine höhere Akkretionsrate aufweisen muss und – aufgrund der ersten Gleichung – dass der Akkretor des leuchtkräftigeren Quasars auch massereicher ist.
In den Gleichungen wurden typische Zahlenwerte für AGN zugrunde gelegt. Theoretische Astrophysiker benutzen meist das cgs-System und geben deshalb Energien nicht in Joule, sondern in erg an. Die Gleichungen besagen nun, dass ein Quasar, bei dem Astronomen eine Leuchtkraft von 1047 erg/s beobachten gemäß Eddingtons Argument ein supermassereiches Schwarzes Loch von 100 Mio. bis einer Mrd. Sonnenmassen beherbergen muss!
Einheitliche Sicht auf Materieaufsammler
Wie im Lexikoneintrag Akkretion besprochen wird, kann man ein vereinheitlichendes Schema vieler akkretierender Quellen schaffen, indem man beobachtete Akkretionsraten in Einheiten der Eddington-Akkretionsrate ausdrückt. Das ermöglicht die reizvolle, globale Sichtweise, dass man stellare und supermassereiche Schwarze Löcher vergleichen kann. Es stellt sich heraus, dass die Quellen zwischen verschiedenen Akkretionszuständen wechseln. Ein Musterbeispiel ist der Röntgendoppelstern Cyg X-1.
Natur mit Kontrollfunktion
Im Prinzip ist die Eddington-Leuchtkraft ein schönes Beispiel, wie die Natur Prozesse von selbst regelt. Denn eine hohe Akkretionsrate bewirkt eine hohe Leuchtkraft. Wird jedoch die Eddington-Leuchtkraft überschritten, sinkt automatisch die Akkretionsrate durch den angestiegenen Strahlungsdruck, so dass die Leuchtkraft wieder sinkt und sub-Eddington wird. Man kann sagen, dass akkretierende Objekte selbstregulierend – autoregulativ – sind.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.