Der Ereignishorizont (engl. event horizon) ist ein bestimmter Typus eines Horizonts, der in der Theorie Schwarzer Löcher und in der relativistischen Kosmologie eine wichtige Rolle spielt.

Horizonte trennen Beobachtbares von Unbeobachtbarem

Wie alle Horizonte trennt er Beobachtbares von Unbeobachtbaren. In der Relativitätstheorie trennt der Horizont Ereignisse (Weltpunkte) von einem Außenbeobachter. Ereignisse sind dabei durch Angabe eines Ortes (drei Raumkoordinaten) und einer Zeitkoordinate charakterisiert. Daher rührt der Name Ereignishorizont.

Schwerkraftfalle Schwarzes Loch

Bei Schwarzen Löchern ist der Ereignishorizont eine ausgezeichnete Fläche, die die echte Singularität umschließt. Anschaulich definiert wird beim Ereignishorizont die Fluchtgeschwindigkeit gleich der Lichtgeschwindigkeit. Weil schon in der Speziellen Relativitätstheorie die Lichtgeschwindigkeit eine Obergrenze für Signale darstellt, die nicht überschritten werden kann, trennt der Ereignishorizont alle Ereignisse, die innerhalb des Horizonts geschehen, von der Außenwelt ab. Deshalb markiert der Ereignishorizont einen Bereich von 'Orten ohne Wiederkehr' (engl. point of no return): Alles, Materie und Strahlung, was sich einem Schwarzen Loch bis zum Ereignishorizont nähert, muss notwendigerweise in die Singularität stürzen. Alle Geodäten zeigen dann nach innen, direkt auf die Singularität. Aus diesem Grund ist der Horizont eine Einfangfläche (engl. trapping surface). Der Einfang ist aber vom Standort des Beobachters abhängig. Die Definition des Horizonts über Einfangflächen führt auf den Begriff des scheinbaren Horizonts.
Erstaunlichweise kommt klassisch – in einer Newtonschen Rechnung – dasselbe Ergebnis zustande, wie korrekt gerechnet mit der Allgemeinen Relativitätstheorie (ART), wenn man den Horizont eines nicht rotierenden Schwarzen Loches berechnen will. Das ist allerdings ein Zufall. Die richtige Mathematik zur Beschreibung von Ereignishorizonten liefert nur die ART.

Gestalt des Horizonts

Horizonte von Schwarzen Löchern sind exakt kugelförmige Regionen, wie die (gleich folgenden) Definitionsgleichungen zeigen. Dies gilt sowohl in der statischen Schwarzschild-Metrik, als auch in der stationären, aber rotierenden Kerr-Metrik. Dennoch wird ein Außenbeobachter eine nicht kugelsymmetrische Form des Horizonts wahrnehmen, falls das Loch rotiert und falls der Beobachter geeignet zum Loch orientiert ist. Dies ist ein Resultat von dem Gravitationslinseneffekt und von dem Frame-Dragging-Effekt.

Horizonte in der Sprache von Einsteins Theorie

Im Unterschied zu 'normalen' Sternen ist der Ereignishorizont nur eine mathematisch definierte Fläche, eine so genannte Nullfläche, die nicht mit einer festen Oberfläche assoziiert ist! In der ART beschreibt man den Ereignishorizont eines rotierenden Schwarzen Loches als zweidimensionale Nullfläche. Sie wird von den beiden Killing-Vektoren aufgespannt. Die Killing-Vektoren folgen wiederum aus der Symmetrie der Raumzeit. Aus der Betrachtung der Isometrien lässt sich die Killing-Gleichung ableiten, deren Lösungen die Killing-Vektoren sind. Weil sie eine Nullfläche erzeugen, heißen sie auch Nullgeneratoren. Die Nullfläche der Kerr-Geometrie ist aufgrund der Isometrien unabhängig von den Koordinaten t (Zeit) und Φ (Azimuthalwinkel). Mit dieser Invarianz sind eindeutig die beiden Symmetrien Stationarität und Axialsymmetrie assoziiert.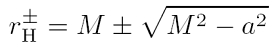
Der Horizontradius berechnet sich aus der Masse des Schwarzen Loches M und dessen spezifischen Drehimpuls a, wie in der Abbildung rechts abzulesen ist. Der Kerrparameter a ist null für 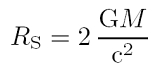die Schwarzschild-Lösung und vom Betrag her M für die maximale Kerr-Lösung (in geometrisierten Einheiten, d.h. wenn G = c = 1). Der Horizont ist für Schwarzschild bei zwei Gravitationsradien oder einem Schwarzschildradius, wie in der zweiten Gleichung links dargestellt ist. Der Schwarzschildradius beträgt einfach nur 2M in geometrisierten Einheiten.

Kerr: Noch ein Horizont!

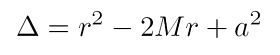Wer gerade aufmerksam die Gleichungen gelesen hat, wird eine Besonderheit bei der Kerr-Geometrie festgestellt haben: zwei Horizonte. Dabei ist der innere Horizont r_- kleiner als der äußere Horizont r₊. Der innere Horizont ist eine so genannte Cauchy-Fläche. Die relativistische Definition der Horizonte ist das Verschwinden des so genannten Delta-Potentials (siehe Gleichung oben rechts). Es handelt sich dabei um eine bestimmte Funktion, wie sie in der Kerr-Geometrie in Boyer-Lindquist-Koordinaten verwendet wird. Weil Delta am Horizont null ist, zeigen die Boyer-Lindquist-Koordinaten leider pathologisches Verhalten an den Horizonten: die Komponente g_rr des metrischen Tensors divergiert und strebt gegen unendlich. Diese Koordinatensingularität (keine 'echte') kann mit anderen Koordinaten, wie den Kerr-Schild-Koordinaten vermieden werden.

Deshalb sieht man schwarz

Das Verschwinden von Delta am Ereignishorizont führt dazu, dass der Rotverschiebungsfaktor dort null wird. Dies ist im Kern der Grund dafür, dass Schwarze Löcher schwarz sind, denn dieser Faktor gewichtet in hoher Potenz jede Emission, die bei Schwarzen Löcher beispielsweise aufgrund der Akkretion entsteht. Diesen gravitativen Effekt auf Strahlung nennt man Gravitationsrotverschiebung. Der Energie- und Intensitätsverlust von Strahlung wird für einen Außenbeobachter am Horizont unendlich stark. Strahlung, die sich knapp vor dem Horizont auf den Weg macht, sieht ein Außenbeobachter extrem gerötet und extrem verdunkelt – aber er sieht sie im Prinzip noch.

rotierender Horizont, aber keiner sieht's!

Der äußere Horizont, den man in der Regel meint, wenn man nur von einem Ereignishorizont spricht, liegt in der Kerr-Metrik mit maximaler Rotation (a = M bzw. a = -M in geometrisierten Einheiten) bei nur einem Gravitationsradius. Der Horizont rotiert wie ein starrer Körper, was ein Unterschied zur differentiellen ('breitenabhängigen') Rotation der Sonne ist. Er reißt bei seiner Drehbewegung alles mit, was Relativisten als Frame-Drag bezeichnen. Diese Korotation mit dem Horizont ist eine wichtige Randbedingung für alle Objekte, die sich dort befinden. Zieht man den Ereignishorizont als Größenkriterium für Schwarze Löcher heran, so sind Kerr-Löcher bei gleicher Masse immer kleiner.

nackte Tatsachen

An sich verhüllt der Ereignishorizont gemäß der kosmischen Zensur (engl. cosmic censorship) intrinsische Singularitäten, wie der englische Mathematiker und Relativist Roger Penrose als Erster vermutet hat. Intrinsisch meint immer 'echte' Singularitäten oder Krümmungssingularitäten, die im Gegensatz zu den Koordinatensingularitäten nicht zu beheben sind. Ein Kuriosum bietet in dieser Hinsicht die extreme Kerr-Lösung: Der innere Horizont ist in diesem Fall (a = M bzw. a = -M), deckungsgleich mit dem äußeren Horizont (siehe Definitionsgleichung oben). Die zentrale Ringsingularität ist in diesem Spezialfall eine so genannte 'nackte Singularität', die von außen sichtbar ist. Solche sichtbaren, unverhüllten Singularitäten sind jedoch verboten. Im Rahmen der ART kann man zeigen, dass durch nackte Singularitäten allerlei Unfug angestellt werden kann, weil sie z.B. das Prinzip der Kausalität verletzen. Beruhigend ist, dass noch kein Astronom eine nackte Singularität in der Natur beobachtet hat. Insofern stützt das die Hypothese von Penrose. In gleicher Weise spricht diese Zensur gegen Weiße Löcher bzw. der einen 'Seite' eines Wurmlochs.
Für Zwischenwerte von a gibt es einen signifikanten Versatz zwischen innerem und äußerem Horizont, der umso größer ist, je näher a der Null kommt. Im Schwarzschild-Fall verschwindet der innere Horizont in der zentralen Singularität bei r = 0. Dies alles fasst eine verlinkte Abbildung zusammen, die beide Horizonte in Abhängigkeit von a illustriert.

Geodäten am Horizont

Am Schwarzschildradius der Schwarzschild-Lösung bzw. am äußeren Horizont der Kerr-Lösung werden alle Geodäten lichtartig! D.h. Strahlung und Materie bewegen sich auf dem Lichtkegel. Man kann sehr leicht nachrechnen, dass alles – Strahlung und Materie – exakt mit der Lichtgeschwindigkeit radial in den Ereignishorizont einfällt. Innerhalb des Horizonts werden die Geodäten raumartig, also tachyonisch.

Evidenzen für den Ereignishorizont?

Die folgende Aussage ist an sich eine Sensation:

Bisher ist es nicht gelungen, bei irgendeinem kosmischen Objekt einen Ereignishorizont nachzuweisen!

Die Astronomen beobachten zwar eine Vielzahl dunkler kompakter Objekte (engl. compact dark object, CDO), doch gibt es mittlerweile zum Schwarzen Loch mit Ereignishorizont Alternativen, z.B. den Gravastern oder den Holostern, die beide ohne Ereignishorizont auskommen. Das ist ein Dilemma in der Physik Schwarzer Löcher! Einschränkend muss gesagt werden, dass bei vielen Loch-Kandidaten die Rotation (durch Eisenlinien oder quasi-periodischen Oszillationen) nachgewiesen wurde. Diese Objekte können zurzeit nur befriedigend als Kerr-Loch, aber nicht durch den Grava- oder Holostern beschrieben werden. Auch die theoretische Astrophysik sieht im Kerr-Loch ein unverzichtbares Objekt, das beispielsweise relativistische Jets antreibt (siehe auch Blandford-Znajek-Mechanismus). Insofern wird von den Astronomen tatsächlich nach wie vor versucht, den Ereignishorizont nachzuweisen. Vom uns am nächsten befindlichen mutmaßlichen Schwarzen Loch im Röntgendoppelstern XTE J1118+480 (Distanz 1.8 kpc) wurde behauptet, dass der Ereignishorizont nachgewiesen wurde (McClintock et al. 2004, astro-ph/0403251). Die Argumentation beruht darauf, dass eine thermische Strahlungskomponente, wie sie in einem Neutronenstern (der eine feste Oberfläche hat) auftritt, fehlt. Sie solle durch die starke Gravitationsrotverschiebung in der Nähe des und am Ereignishorizont stark unterdrückt werden. Die Argumentation dieser Autoren ist jedoch in der Fachwelt umstritten: So behaupten hingegen Abramowicz und Kollegen (A&A 396, L31, 2002) sinngemäß,

..., dass es prinzipiell unmöglich sei, den Ereignishorizont mittels elektromagnetischer Strahlung nachzuweisen!

Die einzige Hoffnung besteht nach den Verfechtern dieser Gegenposition in Gravitationswellen, deren Wellenform in eindeutiger Weise von einem Ereignishorizont zeugen könnten. Diese Sichtweise untermauert eine recht aktuelles Papier von Berti & Cardoso (2006, gr-qc/0605101). Anmerkung des Autors: Falls Sie mich fragen, so teile ich die Position von Abramowicz und Kollegen.

Hoffnungsträger Radioastronomie

Innerhalb der nächsten fünf bis zehn Jahre werden möglicherweise die Radioastronomen den Ereignishorizont und den umgebenden dunklen Bereich direkt abbilden können! Die Radioastronomie erlaubt derzeit die höchste räumliche Auflösung am Himmel, nämlich mittels interferometrischer Methoden wie VLBI bis in den Bereich von Millionstel Bogensekunden. Um eine Vorstellung dieses winzigen Himmelsareals zu bekommen, betrachte man den Vollmond, dessen scheinbarer Durchmesser etwa ein halbes Grad, also 30 Bogenminuten oder 1800 Bogensekunden beträgt. Eine Zerlegung des Vollmonddurchmessers in 1.8 Milliarden gleich große Teile liefert also die Auflösungsgrenze der Radioastronomie!
Favorisierte Kandidaten zur radioastronomischen Abbildung des 'Großen Schwarzen Flecks' (nach der Terminologie meiner Dissertation) um ein Schwarzes Loch sind die zentralen supermassereichen Schwarzen Löcher im Zentrum der Milchstraße in 8 kpc Entfernung (etwa drei Millionen Sonnenmassen schwer) oder im Aktiven Galaktischen Kern von M87 (siehe Arbeiten von Krichbaum et al., MPIfR, astro-ph/0411487, astro-ph/0607072). M87 ist zwar weiter weg (18.7 Mpc), aber dafür ist das zentrale Loch schwerer (drei Milliarden Sonnenmassen), was in einem größeren 'Schwarzen Fleck' resultiert.

Literatur von Andreas Müller zum Thema

In meiner Doktorarbeit (Download PhD, pdf) und einem Konferenzbeitrag (Download Proceeding, pdf) finden Sie viele Einzelheiten zu Schwarzen Löchern und zum Ereignishorizont.
Ich lege in diesen Arbeiten außerdem dar, wie man aus der genauen Gestalt des 'Großen Schwarzen Flecks' nicht nur die Masse des Loches, sondern auch seinen Rotationsparameter und Neigungswinkel zum Beobachter bestimmen könnte.
Die Radioastronomen erreichen im Wellenlängenbereich von Millimetern ein sehr gutes Auflösungsvermögen. Vermutlich wird der Durchbruch in der Radioastronomie gelingen: die erste obskurative Verifikation eines Schwarzen Loches, also der Nachweis eines Lochs durch seine Schwärze.
Inwiefern die (noch hypothetische) Hawking-Strahlung für einen Nachweis taugt (was man als eruptive Verifikation bezeichnen kann), muss noch gezeigt werden. Denn zum einen ist diese Strahlungsform dermaßen schwach, dass sie von anderen Strahlungsformen überstrahlt wird; zum anderen gibt es auch andere thermische Strahlung am Schwarzen Loch, so dass eine überzeugende Beweisführung sehr erschwert wird. In dieser Hinsicht ist die Verfolgung der Experimente an Teilchenbeschleunigern wie dem LHC anzuraten.