Lexikon der Astronomie: f(R)-Gravitation
f(R)-Gravitation ist ein Oberbegriff für gegenüber der Allgemeinen Relativitätstheorie (ART) erweiterte Gravitationstheorien, die außer der Hilbert-Wirkung der ART weitere nichtlineare Terme vorsehen. Diese nichtlinearen Modifikationen werden besonders durch Stringtheorien und M-Theorie motiviert. In der Gravitationsforschung ist allerdings generell von Interesse neue Theorievarianten zu testen – auch, um sich von der Richtigkeit von Bewährtem (in diesem Fall ART und Newtonsche Gravitation) zu überzeugen.
Warum f(R)?
Die Bezeichnung f(R) nimmt Bezug darauf, dass eine wesentliche Grundgleichung dieser Feldtheorie, das so genannte Wirkungsfunktional, eine mehr oder weniger beliebige Funktion des Krümmungsskalars R (= Ricci-Skalars, siehe Ricci-Tensor) sein kann, der sowohl in positiven oder negativen Potenzen, als auch logarithmiert etc. auftreten kann. Die mathematische Symbolik f(R) kann wörtlich als 'Funktion des Ricci-Skalars' übersetzt werden. Die Nichtlinearitäten bewirken anschaulich, dass bei sehr kleinen Krümmungen der Raumzeit plötzlich die neuen Zusatzterme relevant werden können, dass sie aber bei moderaten bis hohen Krümmungen vielleicht völlig irrelevant sind. Dieses seltsame, 'launige' Verhalten liegt in der Natur von Nichtlinearitäten.
Motivation zu einem neuen Ansatz
Das Interesse an solchen Varianten entbrannte, als entdeckt wurde, dass ein solcher f(R)-Ansatz zu beschleunigten Phasen einer sich ausdehnenden Raumzeit führen kann (Alexei A. Starobinsky 1980) – genau das beobachten die Kosmologen für die globale Raumzeit des ganzen Universums. Sollte diese Beschleunigung vielleicht gar nicht durch Einsteins Theorie, sondern vielmehr durch eine f(R)-Gravitation beschrieben werden?
Qual der Wahl
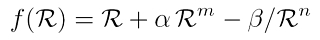 Um diese Frage zu lösen, unternehmen die Gravitationsforscher große Anstrengungen. Aktuell widmen sich zahlreiche Veröffentlichungen ganz unterschiedlichen f(R)-Modellen. Die Forschergruppen setzen ein bestimmte Funktion für f(R) an und betrachten die resultierende Dynamik der modifizierten Feldgleichungen der Gravitation. Eine der vielen f(R)-Familien zeigt z.B. die Gleichung rechts. Darin sind α und β reelle Größen geeigneter Dimension, während m und n beliebige natürliche Zahlen symbolisieren. Die Analyse dieser speziellen Klasse hat ergeben, dass ein solcher Ansatz problematisch und nicht verträglich mit Daten der experimentellen Kosmologie ist (Brookfield et al. 2006).
Um diese Frage zu lösen, unternehmen die Gravitationsforscher große Anstrengungen. Aktuell widmen sich zahlreiche Veröffentlichungen ganz unterschiedlichen f(R)-Modellen. Die Forschergruppen setzen ein bestimmte Funktion für f(R) an und betrachten die resultierende Dynamik der modifizierten Feldgleichungen der Gravitation. Eine der vielen f(R)-Familien zeigt z.B. die Gleichung rechts. Darin sind α und β reelle Größen geeigneter Dimension, während m und n beliebige natürliche Zahlen symbolisieren. Die Analyse dieser speziellen Klasse hat ergeben, dass ein solcher Ansatz problematisch und nicht verträglich mit Daten der experimentellen Kosmologie ist (Brookfield et al. 2006).
Der Übergang zur ART findet bei der Wahl f(R) = R statt, weil dann gerade die Einstein-Hilbert-Wirkung reproduziert wird (siehe dazu auch Olmo 2006, astro-ph/0612047). Dazu muss man wissen, dass die Einstein-Hilbert-Wirkung nur von der Determinante der Metrik – und nicht von weiteren Ricci-Skalaren – abhängt und dass sie über den Euler-Lagrange-Formalismus automatisch auf die klassischen Einsteinschen Feldgleichungen führt.
f(R)-Gravitationen lassen sich generell auf Skalar-Tensor-Theorien reduzieren, also auf Theorien, in denen nicht nur eine tensorielle Größe (wie der metrische Tensor in der ART) die Dynamik bestimmt, sondern auch noch ein zusätzlicher Skalar. Spezielle f(R)-Ansätze sind daher äquivalent zur Brans-Dicke-Theorie.
Ein technischer Aspekt
Technisch unterscheidet man bei der Analyse von f(R)-Modellen zwei Methoden: Den Metrik-Formalismus und den Palatini-Formalismus. Beim Metrik-Formalismus erhält man die Feldgleichungen aus der Variation der Wirkung nach der Metrik. Im Palatini-Formalismus hingegen wird der Ricci-Skalar als Funktion der Zusammenhänge (siehe Christoffel-Symbole) aufgefasst und die Wirkung wird nach Metrik und Zusammenhängen getrennt voneinander variiert.
Stand der f(R)-Forschung
Zielsetzung der f(R)-Gravitationsforschung ist es, die Möglichkeiten neuer Gravitationstheorien durchzuspielen und aus Beobachtungsdaten die entsprechenden Parameter des Ansatzes einzuschränken (im obigen Beispiel also α, β, m und n). Gleich drei f(R)-Familien werden in einem aktuellen Papier von Fay, Tavakol & Tsujikawa (2007) untersucht (Preprint unter astro-ph/0701479).
Zentrale Fragen in der f(R)-Forschung
- Vermag f(R)-Gravitation ein schlüssiges Modell der Inflation zu skizzieren?
- Können f(R)-Ansätze Merkwürdigkeiten wie die Dunkle Energie oder die Pioneer-Anomalie erklären?
- Leistet f(R)-Gravitation mehr als die ART?
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.