Die Feynman-Diagramme oder Feynman-Graphen sind von enormer Relevanz in der Teilchenphysik und Quantenfeldtheorie. Der theoretische Physiker, Nobelpreisträger und geniale Kommunikator Richard P. Feynman (1918 – 1988) erfand sie im Rahmen der Entwicklung der Quantenelektrodynamik. Sie illustrieren Teilchenwechselwirkungen und sind daher ein einfaches Modell, um sich die Kräfte zwischen Teilchen zu veranschaulichen. Feynman-Diagramme stellen gewissermaßen Weg-Zeit-Diagramme dar: die Zeitachse zeigt senkrecht nach oben, die Raumachse waagerecht nach rechts. Weil diese Achsen Konvention sind, werden sie fast ausschließlich weggelassen.

So liest man ein Feynman-Diagramm

Die Teilchen werden als Linien dargestellt, die sich an Wechselwirkungspunkten (Vertices, Einzahl: Vertex) schneiden. Die Wechselwirkung findet dann an einem ausgezeichneten Raum-Zeit- oder Weltpunkt statt. Man hat zur Darstellung der Teilchen folgende Vereinbarungen getroffen:

• Durchgezogene, gerade Pfeile kennzeichnen alle Fermionen. Ungerade Linien repräsentieren die Bosonen (Ausnahme ist das Higgs-Teilchen, s.u.). Die Pfeilrichtung bei Antiteilchen ist umgekehrt zu den normalen Teilchen, weil sich Antiteilchen 'rückwärts in der Zeit bewegen'.
• Wellenförmige Linien verwendet man für das Photon der Quantenelektrodynamik und die Weakonen der schwachen Wechselwirkung.
• Schraubenförmige Linien verwendet man für die Gluonen der Quantenchromodynamik (QCD).
• Gestrichelte Linien sind normalerweise dem Higgs-Teilchen vorbehalten.

Rätselhafte Hieroglyphen am Feynman-Graphen

Diese Konventionen werden nicht immer so rigide eingehalten. In der Regel stehen die Teilchensorten immer an den Linien. Jedes Teilchen hat ein internationales Symbol: γ für das Photon; g für die Gluonen; W⁺, W^- und Z für eines der Weakonen, e^- für das Elektron; e⁺ für das Positron, ν für die Neutrinos (meist mit Index für eine der drei Leptonenfamilien); l für ein Lepton; q für ein Quark; p für ein Proton; n für ein Neutron; K für ein Kaon; π für ein Pion; χ für das Neutralino uvm.

Vertices & Wirkungsquerschnitte

Die Feynman-Graphen bestehen aus Grundelementen, die zu verschiedenen Wechselwirkungsszenarien zusammengesetzt werden können. So existieren Fermion-Boson- und Boson-Boson-Vertex. Mindestens zwei dieser Vertizes konstituieren zu einem Wechselwirkungsereignis. Der Austausch eines virtuellen Bosons, wie den Eichbosonen irgendeiner der vier Wechselwirkungen, wird durch den Propagator dargestellt. Die Teilchenphysiker sind immer an Wahrscheinlichkeitsamplituden interessiert, deren Quadrate den Wirkungsquerschnitt bilden. Letzterer steht für die Wahrscheinlichkeit des gesamten Wechselwirkungsprozesses. Die Amplituden sind proportional zur Kopplung und zum Propagator, der durch eine Greensche Funktion dargestellt werden kann. Dieser Formalismus führt schnell auf die bekannten Streuformeln für Rutherford-Streuung und Mott-Streuung.

Endlich mal ein Beispiel

Die Abbildung rechts zeigt das Feynman-Diagramm des β^--Zerfalls auf der Quark-Ebene: Durch den Austausch eines negativen W-Bosons wandelt sich ein d-Quark im Neutron zu einem u-Quark um. Das ändert den Quarkgehalt dieses Baryons und führt dazu, dass das Neutron (udd) im Atomkern zu einem Proton wird (uud). Da bestimmte Quantenzahlen, wie z.B. elektrische Ladung, Leptonenzahl sowie Energie und Impuls, bei diesem Vorgang erhalten sein müssen, bilden sich im Beta-Zerfall auch neue Teilchen: ein Elektron (β-Strahlen) und ein Anti-Elektron-Neutrino. Auf diese Art und Weise lassen sich sämtliche Teilchenreaktionen darstellen.

Strahlungskorrekturen

Es stellt sich heraus, dass es auch Feynman-Diagramme höherer Ordnung gibt. Diese weisen so genannte Strahlungskorrekturen auf, die man wie folgt klassifiziert:

• photonische Strahlungskorrekturen z.B. Bremsstrahlung,
• nicht-photonische Strahlungskorrekturen mit Vertex- oder Propagator-Korrekturen (Schleifen oder loops), die von virtuellen Teilchen- und Teilchenpaaren herrühren,
• und schließlich QCD-Strahlungskorrekturen, bei denen Vertexkorrekturen und Korrekturen durch die Abstrahlung von Gluonen eingehen.

Noch ein komplizierteres Beispiel

Die zweite Abbildung zeigt gerade einen Feynman-Graph höherer Ordnung mit einer Schleife aus einem Elektron-Positron-Paar.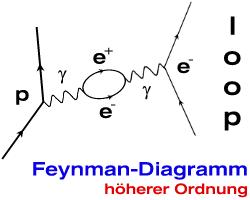
Alle Strahlungskorrekturen bewirken, dass der Wirkungsquerschnitt, also die Wahrscheinlichkeit für das Eintreffen der Teilchenwechselwirkung, verändert wird. Die Teilchenphysiker sind gerade an diesen Wirkungsquerschnitten interessiert und berechnen sie für eine Vielzahl verschiedener Feynman-Graphen.

Der eigentliche Clou

Die Feynman-Diagramme sind jedoch weit mehr als eine anschauliche Darstellung von Teilchenprozessen. Die Teilchenphysiker können sie Bausteinen gleich in Fragmente zerlegen, die jeweils eindeutig mit mathematischen Gleichungen verknüpft sind. Auf diese Weise kann man aus vielen Feynman-Diagrammen niedrigster bis höherer Ordnung Gleichungen ableiten, die die Wirkungsquerschnitte liefern. Das ist das eigentlich Geniale an Feynman-Diagrammen!