Gravitationswellen sind Wellen, die von beschleunigten Massen erzeugt werden. Man stellt sich darunter eine 'Delle' in der gekrümmten Raumzeit vor, die sich mit Lichtgeschwindigkeit fortpflanzt. Wie alle Wellen transportieren auch Gravitationswellen Energie und Informationen, insbesondere Informationen über sich ändernde Krümmungseigenschaften der Raumzeit. Informationen tragen alle Wellen in Form von Richtung, Polarisation, Frequenz (alternativ als Wellenlänge oder Energie) und Intensität (Wellenamplitude) mit sich. Gravitationswellen stehen in wunderbarer Analogie zu den elektromagnetischen Wellen der klassischen Elektrodynamik, die von beschleunigten, elektrischen Ladungen ausgesandt werden.

Hier lauert ein Nobelpreis

Energie wird gerade umgesetzt, wenn Gravitationswellen auf Materie treffen. Sie dehnen und stauchen diese Materiekonfiguration. Diese Deformation geschieht nicht nur in der Raumdimension, sondern auch in der Zeit. Denn die Welle ist dynamische Raumzeit, ein vierdimensionales Kontinuum, das sich fortpflanzt. Die deformierende Auswirkung auf Testkonfigurationen möchten Physiker gerade ausnutzen, um Gravitationswellen zu messen. Bislang ist dies nicht auf direktem Wege gelungen, aber indirekt!

Auf Einsteins Pfaden

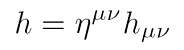Die Existenz von Gravitationswellen oder auch Gravitationsstrahlung genannt geht auf die Pionierarbeit von Albert Einstein (1916) zurück. Er hat die nicht-linearen Feldgleichungen seiner Allgemeinen Relativitätstheorie (ART) linearisiert und auf Wellengleichungen reduziert. Es folgt nun eine Skizzierung der mathematischen Prozedur im Tensorformalismus der ART (in voller Schönheit, siehe z.B. MTW, Gravitation):

• Wir starten mit einem Ansatz für die Metrik, deren raumzeitliche Schwingung gerade der Gravitationswelle entspricht. Sie soll nicht wesentlich von einer flachen Raumzeit (mit Krümmung null) abweichen. Demnach setzt man den metrischen Tensor mit der Minkowski-Metrik an, die ja eine flache Metrik beschreibt; wir ergänzen sie jedoch mit einem Zusatzterm, einer linearen Korrektur ('Störung'). Dieser lineare Ansatz für die Metrik ist eine Näherung schwacher Gravitationsfelder.
• Diesen Ansatz für den metrischen Tensor stecken wir in die Einsteinschen Feldgleichungen. Warum? Weil sie die Dynamik der Gravitationswelle beschreibt. Damit wir die Metrik einsetzen können, müssen sämtliche darin enthaltene Größen ausgerechnet werden: die Christoffel-Symbole, der Riemannsche Krümmungstensor und der daraus resultierende Einstein-Tensor.
• Außerdem verschwindet die rechte Seite der Feldgleichungen (Energie-Impuls-Tensor ist null), weil sich zunächst die Gravitationswellen nur im Vakuum ausbreiten mögen.
• Jetzt wird es kompliziert: Die resultierende Metrik, die die Minkowski-Metrik korrigiert, ist nicht eindeutig festgelegt. Wie in der Elektrodynamik gibt es eine Eichfreiheit, die man ausnutzen kann, um die Einsteinschen Feldgleichungen zu typischen Wellengleichungen zu reduzieren. 'Typisch' heißt hier, dass der d'Alembert- oder 'Quabla-Operator' – natürlich in seiner relativistischen Form – als Differentialoperator auftritt. Wie üblich symbolisieren wir ihn durch ein Quadrat. Sowohl der Krümmungstensor, als auch der Einstein-Tensor erweisen sich als eichinvariante Größen. Die Eichungen in der Theorie der Gravitationswellen nennt man Einstein-, Lorentz-, Hilbert-, Fock- oder de-Donder-Eichung. Die hier gemeinte Lorentz-Eichung ist das gravitative Analog zur Lorentz-Eichung der Elektrodynamik in flacher Raumzeit.

Was tun mit der Wellengleichung?

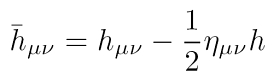Der Formalismus offenbart, dass (analog zur Elektrodynamik) viele Tensorfelder eine Wellengleichung erfüllen: Nicht nur die neu eingeführte Variable in der Gleichung links, auch die Störung der Metrik selbst und vor allem der Riemannsche Krümmungstensor in linearisierter Form genügen einer homogenen Wellengleichung mit d'Alembert-Operator! Die Wellengleichung ist rechts dargestellt. Die Tatsache, dass der Krümmungstensor, der die Existenz und Krümmung des Gravitationsfeldes beschreibt, selbst eine Wellengleichung erfüllt, beweist, dass sich Gravitationseffekte in Form einer Gravitationswelle mit der Lichtgeschwindigkeit c ausbreiten.
Es sei betont, dass diese lineare, relativistische Gravitationstheorie nur einen Ausschnitt der wesentlich komplizierteren, nicht-linearen Gravitationswellenphysik bietet. Die Fortpflanzung der Gravitationswellen in der Nähe starker Gravitationsquellen bzw. in medium ist ein übergeordnetes, komplexeres Regime!
In dieser linearisierten Theorie kann man ebene Wellenlösungen finden, indem man für die zeitlich und räumlich variierenden Tensorfelder die üblichen Wellenlösungen analog zur Elektrodynamik oder klassischen Mechanik ansetzt: eine ebene Welle, geschrieben als Amplitude multipliziert mit einem Exponential mit imaginärem Argument und dem Produkt aus 4er-Wellenvektor und 4er-Ortsvektor.

Lieber TT eichen, als TT fahren

Dieser Ansatz macht eine weitere Eichung nötig, die man transversale, spurfreie Eichung (engl. transverse traceless gauge, TT gauge) nennt. Dabei werden dem Tensorfeld der Wellengleichung weitere Bedingungen auferlegt, wobei nur seine räumlichen Komponenten ungleich null, divergenzfrei und spurfrei sind. In der TT-Eichung gibt es keinen Unterschied mehr zwischen dem Tensorfeld h und der neu eingeführten Variable (vergleiche 3. Abb.)! Alle Tensoren, die den Bedingungen der TT-Eichung genügen, nennt man TT-Tensoren. Die Transversalität ist auf die Tatsache, dass die Gravitationswelle senkrecht zur eigenen Ausbreitungsrichtung räumlich oszilliert zurückzuführen (Nachweis durch Bildung des Produkts aus Tensorfeld h und 4er-Wellenvektor).

Auch aus einfachen Ansätzen ohne TT-Eichung (eindimensionale, zeitlich variable Wellen) resultieren ebene Gravitationswellen, die sich in eine bestimmte Richtung fortpflanzen. Zu diesen Tensorfeldern lassen sich Linienelemente zuordnen, die gerade als raumzeitlich variierende Gravitationswellen interpretiert werden können.

Gravitationswellen haben zwei Polarisationen

Man kann nun die Linienelemente ausnutzen, um zu beschreiben, was geschieht, wenn Gravitationswellen auf eine Konfiguration von Testteilchen treffen. Dann zeigt sich in verschiedenen Fallstudien, dass Gravitationswellen transversale Wellen sind und zwei Polarisationszustände besitzen, die sich um 45? unterscheiden. Anders gesagt, hat das Gravitationsfeld zwei Strahlungsfreiheitsgrade, ist also eine Tensorwelle mit Spin 2. Die Gezeitenkräfte wirken senkrecht zur Ausbreitungsrichtung der Welle. Treffen linearisierte, ebenfrontige Gravitationswellen auf einen Ring aus Testteilchen, so geschieht eine Quadrupoldeformation: der Ring wird zunächst in einer Ebene in eine Ellipse, dann wieder in einen Ring und wiederum in eine Ellipse deformiert (illustriert in Animation).
Als Maß für die Stärke einer Gravitationswelle, die Amplitude, kann die Deformation des Rings mit Radius R zu einer Ellipse entlang der kürzeren Halbachse um dR dienen. Ein größerer Wert dR/R spricht demnach für eine stärkere, intensivere Welle. Eine typische Größenordnung der absoluten Längenänderung dR ist 10^-21 Meter! Diese winzige Längenskala stellt die Messtechnik vor enorme Anforderungen. Im Wesentlichen ist dies die Ursache dafür, dass Gravitationswellen bisher nicht direkt mit einem Detektor gemessen werden konnten.

Woher kommen Gravitationswellen?

Als kosmische Quellen für Gravitationswellen kommen im Prinzip alle beschleunigten Massen in Frage. Die uns umgebende Raumzeit ist also nur in erster Näherung flach: vielmehr handelt es sich um ein ständig schwingendes, raumzeitliches Gebilde, in dem Gravitationswellen verschiedener Intensität und Frequenz interferieren. Zur Messung dieser Ereignisse gibt es nur eine Komplikation: die Raumzeit ist ein sehr starres Gebilde, und es sind enorme Massenbeschleunigungen nötig, um sie signifikant zum Schwingen zu bringen und so einen Detektornachweis zu erbringen. Aus diesem Grund kommen nur extreme Ereignisse im Kosmos in Betracht. Diese Quellen werden nochmals nach dem Zeitverhalten des Signals unterschieden: Einmalige Ereignisse nennt man Burst-Quellen. Daneben gibt es regelmäßig zeitlich wiederkehrende Ereignisse von periodischen Quellen.

starke kosmische Gravitationswellen-Emitter

• Supernova-Explosionen (Typ II),
• kompakte Objekte in einem Mehrfachsystem, z.B. ein Doppelsternsystem aus zwei Neutronensternen (NS) oder stellaren Schwarzen Löchern (SL), also kompakten Binären (engl. compact binaries),
• entstehende kompakte Objekte im Gravitationskollaps,
• verschmelzende kompakte Objekte, insbesondere NS-NS-, NS-SL-, SL-SL-Verschmelzung,
• supermassereiche Schwarze Löcher in den Kernen von Galaxien (siehe auch Aktive Galaktische Kerne), die Masse durch Akkretion aufnehmen
• verschmelzende supermassereiche Schwarze Löcher in den Kernen von Galaxien
• oder die Entstehung des Universums im Urknall. Die Astronomen gehen davon aus, dass man mit Gravitationswellen noch tiefer in die Frühphasen des Universums schauen kann, als mit elektromagnetischen Wellen. Die natürliche, elektromagnetische Barriere der Rekombinationsära bei einer Rotverschiebung von z ~ 1100 bzw. etwa 400000 Jahre nach dem Big Bang ist 'transparent' für Gravitationswellen. Die Kosmologen hoffen, dass die Gravitationswellen aus dem frühen Kosmos das dichte, frühe Universum mehr oder weniger unbeeinflusst passiert haben und so wertvolle Informationen über die Entstehung unserer Universums bis zur Erde tragen können. Die Astronomen erwarten die Existenz eines Gravitationswellenhintergrunds, der als gravitatives Analogon zur kosmischen Hintergrundstrahlung zu betrachten ist.

Wie schnell zappelt eine Gravitationswelle?

Die Frequenzen der Gravitationswellen dieser Quellen sind sehr unterschiedlich und streuen nach aktuellen Berechnungen im Bereich von acht Größenordnungen, von 10^-4 bis 10⁴ Hz. Die niedrigsten Frequenzen im mHz-Bereich werden von umeinander kreisenden kompakten Binären erwartet. Doppelsternsysteme aus Weißen Zwergen tragen so zu einem kontinuierlichen Brummen im All bei. In der Gravitationswellenastronomie nennt man das Untergrundrauschen. Die Frequenz von verschmelzenden stellaren Schwarzen Löchern liegt bei ziemlich genau einem Millihertz, die Entstehung eines stellaren Schwarzen Lochs bei etwas höheren Frequenzen (engl. chirp: 'Zirpen', 'Zwitschern'). Bei 10^-2 Hz liegt die Frequenz von Gravitationswellen aus einem Doppelsystem mit zwei massereichen Schwarzen Löchern von 100 000 Sonnenmassen. Eine solche Konfiguration ist vorstellbar, wenn ganze Galaxien miteinander verschmelzen und sich deren Kerne annähern. Die ULIRG NGC 6240 ist ein favorisierter Kandidat für ein solches doppeltes, massereiches Schwarzes Loch (Arbeiten von Stefanie Komossa, MPE).
Die Frequenz erhöht sich im entwickelnden Binärsystem aus kompakten Objekten infolge der Abstrahlung von Energie und wird schließlich besonders groß, etwa 10 bis 100 Hz, im 'Showdown', wenn sie verschmelzen. Die höchsten Frequenzen erwartet man bei der klassischen Kernkollaps-Supernova (engl. core collapse SN), also SN Typ II: Bei dieser Burst-Quelle liegen die erwarteten Frequenzen bei einem bis 10 kHz (Quelle: Website des deutschen Gravitationswellendetektors GEO 600).
Der mHz-Frequenbereich ist prinzipiell terrestrisch nicht beobachtbar. Erst weltraum-gestützte Laser-Interferometrie wird dieses Beobachtungsfenster öffnen. Dies ist die Motivation für das multinationale Projekt LISA (engl. Akronym für Laser Interferometer Space Antenna), einer Anordnung aus Laserinterferometern, die im Weltraum Gravitationswellen messen soll!
Das Beobachtungsfenster auf der Erde öffnet sich erst ab einer Frequenz von etwa 10 Hz. Die Komponenten eines Doppelsternsystems nähern sich mit der Zeit immer mehr an, was die Frequenz der Gravitationswellen nach und nach erhöht. Kurz vor dem Kollaps des Binärs, d.h. dessen Verschmelzung, beträgt die Frequenz etwa 40 Hz und ist damit irdisch beobachtbar.

Zentrum deutscher Gravitationsforschung

In Deutschland sitzen die Experten für Gravitationswellen in Theorie und Experiment am MPI für Gravitationsphysik, das auch Albert-Einstein-Institut (AEI) genannt wird. Die Abteilung für Theorie befindet sich in Golm bei Potsdam, während die Experimentatoren und der L-förmige Gravitationswellendetektor in der Nähe von Hannover untergebracht sind. Das AEI entwickelt Datenanalyse-Verfahren für GEO 600 und LIGO. Außerdem berechnen die Gravitationsforscher am AEI theoretische Simulationen von umkreisenden und verschmelzenden kompakten Binären auf Supercomputern exzessiv behandelt. Am AEI beschäftigt man sich auch mit anderen Forschungsgebieten der Gravitation, neben Gravitationswellen. Wie an den meisten Forschungsinstituten wird eine enge, internationale Zusammenarbeit gepflegt.

Es geht komplizierter...

Die allgemeine Behandlung und Wechselwirkung von Gravitationswellen ist sehr kompliziert, wie der obige, mathematische Abriss sicherlich andeutet (obwohl dieser vereinfachend war: im Limes schwacher Gravitationsfelder und im Vakuum). Natürlich sollte die Energie, die die Gravitationswellen mit sich tragen, die Raumzeit selbst krümmen, ein Effekt, der in der linearisierten Theorie vernachlässigt wird. Außerdem verändern Gravitationswellen ihre Gestalt, wenn sie durch ein mit Materie gefülltes Medium propagieren, was man in Analogie zu elektromagnetischen Wellen als 'Brechung' bezeichnen könnte.
Auch in Abwesenheit von Materie und einer Region, die nur von Gravitationswellen durchsetzt ist, können seltsame Dinge geschehen: Bei bestimmten Wellenlängen und Amplituden kann ein Gravitationswellenpuls kollabieren und eine Singularität hinterlassen: solche Brill-Wellen können aus reiner Gravitationsenergie, ein Schwarzes Loch erzeugen!
All diese Effekte verdeutlichen, dass eine tief gehende theoretische Behandlung nur mithilfe von Methoden der Numerischen ART möglich ist. Dann gelingt auch eine approximative Beschreibung von Quellen der Gravitationswellen. Ein mathematischer Zugang besteht z.B. darin, dass jede beliebige Massenverteilung durch elementare Quellen, den Multipolen, darstellbar ist. Eine Multipolentwicklung in einer geeigneten Basis ist mit den Kugelflächenfunktionen (engl. spherical harmonics) sehr elegant möglich. Die Kugelflächenfunktionen bilden eine orthonormierte Basis auf der Einheitskugel. Damit eignen sie sich hervorragend, um beliebige Verteilungen auf Kugelschalen mathematisch darzustellen. In der Kosmologie nutzt man das aus, um die Verteilung der kosmischen Hintergrundstrahlung auf der Himmelskugel zu beschreiben. Dieses Verfahren ist auch aus der klassischen Elektrodynamik bekannt, um beliebige Ladungsverteilungen und deren Feldverteilungen im Umgebungsraum zu beschreiben. Außerdem erweist sich diese Methode sehr brauchbar bei der Behandlung des quantenmechanischen Wasserstoffsproblems (siehe Quantentheorie) und in der Kern- und Solarphysik. Es ist eine fundamentale Methode, die in sehr vielen Bereichen der Physik Anwendung findet.
Im Prinzip gibt es beliebig viele Multipole, die in der Reihenentwicklung durchnummeriert und bezeichnet werden (Monopol, Dipol, Quadrupol, Oktupol, Hexadekapol etc.). Numerisch interessant wird es dann, wenn aufgrund der Symmetrie der Massenverteilung bestimmte Terme herausfallen oder nach Erreichen einer bestimmten Genauigkeit die Reihenentwicklung abgebrochen werden darf.

Anwendung in der Pulsarphysik

Auf diese Weise ist es möglich einen Binärpulsar relativ einfach durch Multipole zu beschreiben. Dabei unterliegt das Quadrupolmoment einer sehr starken zeitlichen Änderung, weshalb die Abstrahlung von Gravitationswellen hier äußerst effektiv ist. Die so genannte Quadrupolformel ist eine der wenigen Formeln der Physik mit dritter Zeitableitung. Indirekt (!) wurden auf diese Weise Gravitationswellen bereits nachgewiesen: Die Emission von Gravitationswellen reduziert in einem Doppelsternsystem die Rotationsenergie des Systems. Infolge dieses Energieverlusts müssen sich die Sterne sukzessiv annähern. Im Prinzip geschieht diese Abstrahlung bei allen Doppel- und Mehrfachsternsystemen. Besonders effizient ist sie jedoch nur bei engen, kompakten Binären. Der Binärpulsar PSR1913+16 ist 25 000 Lj entfernt und erzeugt eine sehr hohe Abstrahlungsleistung bei Gravitationswellen, nämlich fast 10⁴⁵ Watt! Diese hohe Leistung beruht auf der Kompaktheit der Neutronensterne (etwa 1.4 Sonnenmassen mit je nur ca. 20 km Durchmesser) und der des Systems (Umlaufzeit von nur acht Stunden). Nur eine Komponente pulsiert nachweislich. Die Verkürzung der Umlaufzeit durch Abstrahlung von Gravitationswellen und damit die Reduktion der Pulsperiode kann hervorragend durch die Allgemeinen Relativitätstheorie beschrieben werden. Die Astronomen Russel A. Hulse und Joseph H. Taylor Jr. bekamen für ihre Langzeitbeobachtung und deren Interpretation 1993 den Nobelpreis für Physik. Ihr beobachteter Binärpulsar wird auch häufig als Hulse-Taylor-Pulsar bezeichnet. Die Beobachtung war nicht nur ein weiterer Erfolg für die ART, sondern auch für die Gravitationswellenastronomie. Der indirekte Nachweis spornt seither viele Kollaborationen an, die Gravitationswellen auch auf direktem Wege zu entdecken (siehe unten).

Pionier des Gravitationswellenexperiments

Experimentell wurde erstmals 1969 von J. Weber der Versuch unternommen, Gravitationswellen direkt nachzuweisen. Das Messprinzip beruhte darauf, dass die Wellen die Anordnung von Testteilchen deformieren und die Teilchen dadurch relative Beschleunigungen erfahren. Weber benutzte einen anderthalb Tonnen schweren Zylinder aus Aluminium, der mit Piezosensoren bestückt war und beim Durchgang von Gravitationswellen in Schwingungen versetzt werden sollte. Dieses Phänomen ist vergleichbar mit einer Glocke, die man anschlägt und die dann in Schwingungen gerät. Um lokale Störeffekte ausschließen zu können, wurden zwei dieser Detektoren in 1000 km Abstand aufgestellt. Tatsächlich soll Weber Signale aus dem Galaktischen Zentrum detektiert haben, was aber nicht reproduziert werden konnte. Die Empfindlichkeit dieser Zylinder-Detektoren ist außerordentlich gering; außerdem reagieren sie nur auf eine bestimmte Frequenz von Gravitationswellen.

Laser-Interferometrie

Viel günstiger ist dagegen eine optische Anordnung aus Laser-Interferometern. Solche Messapparaturen beruhen auf dem klassischen Michelson-Interferometer (Abbildung). Es ist bizarr, dass diese Messapparatur, die 1881/87 Einstein zur Entwicklung der Speziellen Relativitätstheorie bestärkte nun dazu benutzt werden soll, um die letzten Geheimnisse der Allgemeinen Relativitätstheorie nachzuweisen.
Im experimentellen Aufbau von Laser-Interferometern wird ein sehr stabil laufender Festkörper-Laser dazu verwendet, um das infrarote Laserlicht mithilfe eines halbdurchlässigen Spiegels auf zwei optische Laufstrecken (so genannte Arme) aufzuteilen. Diese Arme bilden üblicherweise ein großes L. Am Ende dieser Strecken wird der Teilstrahl jeweils an einem weiteren Spiegel total reflektiert und wieder zu dem Ort geleitet, wo sich die beiden Teilstrahlen bildeten. Dort werden die Teilstrahlen überlagert. In der Physik nennt man die Überlagerung von Lichtwellen Interferenz. Interferierende Wellen bilden eine charakteristisches Interferenzmuster und können sich (bei gleicher Wellenlänge) auslöschen, wenn 'Wellenberg auf Wellental' trifft (destruktive Interferenz) oder verstärken, wenn 'Wellenberg auf Wellenberg' trifft (konstruktive Interferenz). Im Gravitationswellendetektor stellen die Forscher das optische System im normalen Modus so ein, dass durch destruktive Interferenz kein Licht sichtbar ist. Dort, wo die interferierenden Strahlen ausgekoppelt werden, ist es dunkel. Trifft nun eine Gravitationswelle senkrecht auf die Ebene, in der die Arme des Interferometers liegen ein, so wird ein Arm (oder beide, je nach Einfallsrichtung) periodisch verkürzt und verlängert. Dies ändert die Bedingung für destruktive Interferenz, so dass plötzlich ein Signal am vormals dunklen Auskopplungsort erzeugt werden muss: die Gravitationswelle würde gemessen!
Das hört sich alles ganz toll an. Aber die messtechnische Herausforderung lässt sich pointiert wie folgt darstellen: die Interferometrie dient der Messung eines Gangunterschieds, also einer sehr kleinen relativen Längenänderung. Diese wurde mit einer Obergrenze zu 10^-18 abgeschätzt. Bezogen auf die mittlere Armlänge von 3 km (wie bei LIGO, siehe unten) bedeutet dies, eine Länge unterhalb der Ausdehnung der Nukleonen im Atomkern messen zu wollen! Oder genauso unglaublich veranschaulicht: Auf der Länge eines Lichtjahres entspricht die Längenänderung aufgrund einer durchlaufenden Gravitationswelle dem Durchmesser eines menschlichen Haares! Daher ist klar, dass der Trend zu größeren Armlängen geht. Dies kann künstlich durch Mehrfachreflexionen des Laserstrahls innerhalb der optischen Kavität erreicht werden. Das Großprojekt LISA geht sogar in den Weltraum und kann die Armlänge eklatant steigern.

Lokalisierung der Quelle

Weltweit existieren eine ganze Reihe von Projekten, die auf dem Interferometrie-Prinzip beruhen und sich im Wesentlichen nur durch die Armlängen unterscheiden. Eine Zahl von mindestens zwei Apparaturen ermöglicht die Lokalisierung des Entstehungsortes der Gravitationswelle an der Himmelssphäre. Außerdem verbessert es die Messstatistik und reduziert den Einfluss von (lokalen) Störsignalen. Das 'Rauschen' durch störende, lokale Einflüsse wie Straßenverkehr, Flugzeuge, Erdbeben etc. kann durch globale Messungen an verschiedenen Orten der Erde minimiert werden. Die Planung sieht vor, die internationalen Projekte zu koppeln, den Datenaustausch zu bewerkstelligen und so Gravitationswellenastronomie im großen Stil zu betreiben. Das Konzept und auch dessen hohe, organisatorische Anforderungen ist damit der Very Long Baseline Interferometry (VLBI) der Radioastronomie ähnlich.

Geplante und im Bau befindliche Laser-Interferometer

• GEO 600 mit 600 m Armlänge bei Hannover, BRD. Die deutsch-britische Kollaboration nimmt bereits Messungen auf.
• VIRGO mit 3 km Armlänge, die künstlich durch Mehrfachreflexionen auf 120 km gesteigert werden kann. Die französisch-italienische Kollaboration mit Standort nahe Cascina bei Pisa erreicht eine gute Empfindlichkeit im Bereich zwischen 10 und 1000 Hz der Gravitationswellen.
• TAMA 300 mit 300 m Armlänge in Japan. Das Projekt existiert seit 1995 und nutzt Fabry-Perot Michelson Interferometer zur Messung von Gravitationswellen.
• Australian International Gravitational Observatory, AIGO hat 80 m Armlänge und befindet sich in Australien.
• Laser Interferometer Gravitational Wave Observaotory, LIGO. LIGO ist ein Laserinterferometer mit 4 km Armlänge der USA. Die erste Anordnung wird mittlerweile verbessert: LIGO-II ist um einen Faktor 10 empfindlicher als LIGO-I.
• Laser Interferometer gravitational-wave Small Observaotory in a Mine, LISM, ist unterirdischer Detektor (1000 m Tiefe) in der Kamioka-Mine (wo sich auch der berühmte NeutrinodetektorSuper-Kamiokande befindet) in Japan. LISM ist mit 20 m Armlänge zwar deutlich kleiner als konkurrierende Gravitationswellendetektoren, aber aufgrund seiner Abschottung durch das Gestein und seiner relativ erdbebensicheren Lage sehr empfindlich. Bislang wurde die Empfindlichkeit für Gravitationswellen mit einem Faktor 100 über derjenigen von LIGO beziffert (April 2004). Das thermische Rauschen wird mit kryogenisch gekühlten Instrumenten unterdrückt. So soll die Empfindlichkeit weiter gesteigert werden, um mit LIGO-II mithalten zu können.
• Laser Interferometer Space Antenna, LISA, ein weltraum-gestütztes Projekt mit 5 Millionen km Armlänge; das entspricht der 13fachen mittleren Entfernung der Erde zum Mond oder fast 17 Lichtsekunden! Dieses europäisch-amerikanische Projekt wird von der ESA und der NASA geplant und gefördert und soll aus drei baugleichen Satelliten bestehen, die ein riesiges, gleichseitiges Dreieck im All bilden und um 20? der Erde hinterher fliegen sollen. Mit diesem Laser-Interferometer der Superlative können sämtliche Gravitationswellen nachgewiesen werden, fast unabhängig von Frequenz und Richtung, weil die Armlänge so unglaublich groß ist und das Dreieck frei im Weltraum drehbar ist. Es ist geplant LISA 2015 zu starten und dann für fünf Jahre Messungen durchzuführen.

Gravitationswellensalat

Es sei auf eine weitere Komplikation bei der Detektion von Gravitationswellenemittern hingewiesen: Es gibt es viele Quellen, deren Signale (mit unterschiedlichen Amplituden und unterschiedlichen Frequenzen) überlappen. Selbst wenn also der Nachweis von Gravitationswellen gelingt, muss aus diesem 'Signalgemisch' die jeweilige Quelle extrahiert werden. Diese Problematik läuft unter dem Begriff 'Quellenverwechslung' (engl. source confusion) und ist ein generelles Problem der beobachtenden Astronomie. Hohe räumliche Auflösung und Frequenzfilter sind dabei die Methoden im elektromagnetischen Sektor, die auf analoge Weise für die Detektion von Gravitationswellen entwickelt werden müssen. Wie aus der bisherigen Betrachtung ersichtlich ist, kann die Armlänge des Interferometers als Frequenzfilter aufgefasst werden.
Trotz einiger aktiver Experimente wurden Gravitationswellen bislang nicht gesichert direkt nachgewiesen. Mit dem Betrieb der neuen Laser-Interferometer sollte dies möglich werden und der Astronomie ein neues Fenster ins All eröffnen: die Gravitationswellenastronomie.