Eine wichtige Größe in der Astronomie, um Sterne zu charakterisieren.

scheinbare vs. absolute Helligkeit

Weil sich die Sterne in unterschiedlichen Entfernungen zur Erde befinden, sagt die beobachtete oder scheinbare Helligkeitm nicht allzu viel über einen Stern aus, wenn man dessen Distanz nicht kennt. Daher ist es immer wichtig, diese aus Methoden der Entfernungsbestimmung zu ermitteln. Astronomen unterscheiden von der scheinbaren die absolute HelligkeitM, die so festgelegt wurde, dass es derjenigen Helligkeit entspricht, wie uns das leuchtende Objekt in einer Entfernung von zehn Parsec erscheinen würde.

Sprengen der klassischen Größenklassen

Historisch bedingt unterschied man die Helligkeiten zunächst in sechs Größenklassen. Der erste Detektor war das menschliche Auge, das sicherlich nicht voll ausgereift ist für astronomische Beobachtungen. Die hellsten Sterne definierte man mit der 1. Größe, die lichtschwächsten, gerade noch mit dem Auge sichtbaren als Sterne 6. Größe. Im Zuge besserer astronomischer Instrumente wurde diese Skala deutlich erweitert. So weisen die leuchtschwächsten Objekte, zum Beispiel extrem weit entfernte Galaxien in Tiefenfeldbeobachtungen wie dem Hubble Deep Field North (HDFN) etwa 30. Größe auf!

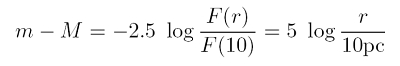
Das menschliche Auge ist ein logarithmischer Strahlungsdetektor, daher ist die natürliche Helligkeitsskala logarithmisch und nicht linear.

Pogson – ein helles Köpfchen

Der britische Astronom Norman Robert Pogson (1829 – 1891) führte 1856 ein logarithmisches Gesetz ein, das den Zusammenhang zwischen scheinbarer Helligkeit m, der Magnitude, und dem Strahlungsfluss F wiedergibt. Dabei zeigte sich, dass das Verhältnis der Strahlungsflüsse aufeinander folgender Größenklassen immer konstant ist, etwa 2.512. Mit der obigen Definition, dass die absolute Helligkeit bei 10 pc zu messen ist, folgt daher die Gleichung oben, das so genannte Distanzmodul. Bei bekannten zwei von den drei Größen lässt sich die dritte arithmetisch ermitteln – also anhand Umstellen der Gleichung berechnen. Eine besonders wichtige Anwendung ist die Entfernungsbestimmung kosmischer Objekte. Die scheinbare Helligkeit m ist immer bekannt, weil man sie am Himmel direkt misst. Das entsprechende Verfahren heißt Photometrie, wörtlich soviel, wie Messung des Flusses der Photonen. In der Regel werden die Helligkeiten in der Einheit ^mag oder ^m für magnitudo angegeben.

Jagd auf Standardkerzen

Kann der Astronom nun die absolute Helligkeit M aufgrund theoretischer Modelle eingrenzen, so kann er über beobachtete, scheinbare Helligkeit m und Distanzmodul direkt die Entfernung r des leuchtenden Objekts ableiten. Diese Prozedur wird bei so genannten Standardkerzen exzessiv angewandt: die Astronomen suchen dabei kosmische Quellen deren intrinsische Helligkeit (die Helligkeit 'vor Ort' der Quelle) sie in irgendeiner Form ableiten können. Prominente Beispiele für Standardkerzen sind Cepheiden und Supernova vom Typ Ia.

Warum der Aufwand?

Die Kenntnis von Entfernungen kosmischer Objekte ist von Belang für alle Disziplinen der Astronomie. Die Entfernungen der Sterne liefern Informationen über Struktur und Aufbau unserer Heimatgalaxie; die Entfernungen der Galaxien geben Aufschluss über Struktur und Aufbau von Galaxienhaufen und -superhaufen; von besonderer Bedeutung sind Entfernungsdaten für die Kosmologie, um die relative, dreidimensionale Anordnung der Objekte im Universum aufzudecken (Stichwort: large scale structure). Daraus folgen die Eigenschaften des Universums, wie z.B. zunächst eine untere Grenze für seine Größe, aber auch seine Krümmung, sein Gehalt an baryonischer Materie, Dunkler Materie und Dunkler Energie oder sogar seine Topologie. Letztendlich verrät das den Kosmologen das Schicksal des dynamischen Universums: wird es sich ewig ausdehnen oder wieder in sich zusammenfallen?

scheinbare Helligkeiten kosmischer Nachbarn

• der Stern Sirius in Canis Major (dt. Großer Hund): m = -1.5
• die Sonne: m = -26.8
• und vom Vollmond: m = -12.5

Achtung Farbe!

Es gibt bei der Messung von Helligkeiten noch eine technische Komplikation: Astronomen messen die Helligkeiten nur in bestimmten Spektralbereichen. Entsprechend definierte man visuelle Helligkeit (V), Blau-Helligkeit (B), Rot-Helligkeit (R), Infrarot-Helligkeit (I), Ultraviolett-Helligkeit (U) etc. Um hier eine Einheitlichkeit zu gewährleisten, benutzt man Filtersysteme, also Filter, die nur einen wohl bekannten Spektralbereich durchlassen (transmittieren). Besonders gebräuchlich in der Astronomie ist das Johnson-Filtersystem (1950), bestehend aus einem UBV-System.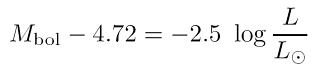
Die gemessenen Helligkeiten in den einzelnen Filtern kann man voneinander abziehen. So erhält den so genannten Farbindex, sehr gebräuchlich beispielsweise B-V. Das Hertzsprung-Russell-Diagramm war historisch ein Farben-Helligkeitsdiagramm und verwendete gerade solche Farbindizes.

Total hell!

Als bolometrische Helligkeit bezeichnet man diejenige Helligkeit die sich ergibt, wenn man allen Helligkeiten der einzelnen Spektralbereiche aufsummiert. Sie ist mit dem totalen, spektralen Fluss assoziiert. Diese Größe ist jedoch keineswegs so leicht der Beobachtung zugänglich. Die absolute bolometrische Helligkeit hängt eindeutig mit der Leuchtkraft zusammen, einer wichtigen Zustandsgröße von Sternen, neben Effektivtemperatur, Spektraltyp, Farbe, Radius, Masse, mittlerer Dichte, Rotation, Magnetfeld, Alter und chemischen Zusammensetzung. Bezogen auf die Daten der Sonne ergibt sich die letzte Gleichung als Zusammenhang zwischen absoluter bolometrischer Helligkeit und Leuchtkraft eines Sterns.