Horizont ist ein Wort, das aus dem Griechischen kommt: Vollständig heißt es eigentlich horizon kyklos und bedeutet 'begrenzender Kreis'. Das führt bereits auf den Inhalt, den man für gewöhnlich mit dem Begriff Horizont verbindet. Ein Beobachter, der sich auf der Erde unter freiem Himmel befindet, sieht den Horizont als Berandungslinie von Erde und Himmel. Diese Peripherielinie hat eine Kreisform, wenn der Beobachter sich um 360 Grad um seinen Beobachtungsort dreht. Präzise lässt sich folgendermaßen formulieren:

Der (scheinbare) Horizont ist die Schnittfigur der Himmelskugel mit einer Ebene, die senkrecht zum Lot durch den Beobachtungsort und durch den Beobachtungsort selbst verläuft.

Das ist eine geometrische Definition. Sie macht klar, dass der Horizont beobachterabhängig ist, weil es darauf ankommt, wo er steht. Sehr allgemein kann man formulieren:

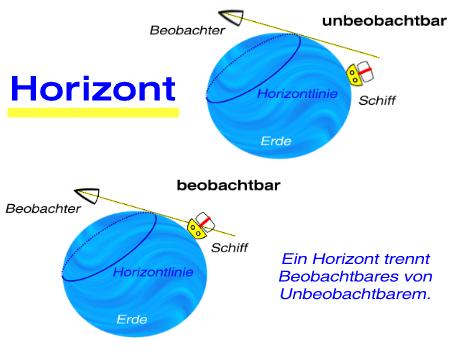
Ein Horizont trennt Beobachtbares von Unbeobachtbarem.

Der vertraute Horizont

Das rechtfertigt den fast tautologischen Begriff Beobachtungshorizont. Sehr anschaulich wird diese Auffassung am Meer, wenn man Schiffe beobachtet. Nehmen wir an, man befinde sich in einem Hafen und beobachte ein auslaufendes Schiff (siehe folgende Illustration). Es ist – gute Sichtbedingungen vorausgesetzt – sichtbar, weil es sich vor dem Horizont befindet. Nun geht das Schiff aber auf eine weite Reise über das Meer. Es entfernt sich vom Beobachter und wird immer kleiner. Das Schiff nähert sich der Horizontlinie. Schließlich verschwindet zuerst der untere Teil des Schiffs, weil die Erdoberfläche gekrümmt ist. So sieht der Beobachter nur noch den Schiffsmast, bis auf derjenige verschwindet. Das Schiff ist nun unbeobachtbar, denn sich unterhalb des Horizonts. Deshalb trennt der Horizont Beobachtbares von Unbeobachtbarem. Wir werden sehen, dass diese Definition auch für andere Horizontbegriffe zutrifft.

Der natürliche Horizont

Eine leichte Modifikation erhält die obige Definition des scheinbaren Horizonts unter Berücksichtigung der lokalen Morphologie der Landschaft. So beeinflussen Berge, Bäume, Gebäude etc. den Verlauf der Horizontlinie. Der daraus resultierende Horizontbegriff heißt natürlicher Horizont.

Der künstliche Horizont

In der Aeronautik ist der künstliche Horizont von Bedeutung. Hier dient die Oberfläche einer Flüssigkeit (Meniskus) als präzise Abbildung der lokalen Horizontalfläche. Mit künstlichen Horizonten wird eine genaue Navigation von Flugzeugen, Schiffen und U-Booten möglich.

Horizonte in der Astronomie

In der Astronomie sind besonders scheinbarer, wahrer und natürlicher Horizont von Belang. Der wahre Horizont unterscheidet sich vom scheinbaren nur dadurch, dass der Bezugspunkt nicht durch den Beobachterstandort (topozentrisches System), sondern durch den Erdmittelpunkt (geozentrisches System) geht. Der Unterschied macht sich nur bei erdnahen Objekten bemerkbar. Der Horizont spielt dann eine Rolle, wenn es um die Sichtbarkeit von Gestirnen geht. Die Erdrotation sorgt für die scheinbare Rotation des Himmelsgewölbes. Deshalb bleiben die Gestirne in der Regel nicht am gleichen Ort. Eine banale Folge dessen ist der Tagbogen der Sonne. Der Lauf der Sonne beschreibt Tag für Tag einen Bogen an der Himmelskugel, dessen Höhe jahreszeitlich variiert (Ursache: Schiefe der Ekliptik). Es gibt jedoch auch exakt zwei Punkte, die ihren Ort trotz Rotation nicht verändern. Diese Fixpunkte nennt man Himmelspole. Man findet sie dort, wo die verlängerte Erdachse das Himmelsgewölbe durchstößt. Auf der Nordhalbkugel ist diesem Fixpunkt der Polarstern (Polaris) im Sternbild Ursa Minor (dt. Kleiner Bär) sehr nahe. Er befindet sich nur 55 Bogenminuten (fast ein Grad) davon entfernt. Es scheint, dass der Rest des Nordhimmels um den Polarstern rotiert, was man eindrucksvoll mit Strichspuraufnahmen in der Astrophotographie demonstrieren kann. Ein Pendant zu Polaris gibt es am Südhimmel nicht. Das Sternbild Crux (dt. Kreuz des Südens) enthält den südlichen Fixpunkt.
Allerdings sind die Fixpunkte nicht ganz fix: Die Erde ist ein Kreisel und unterliegt wie jeder rotierender Körper der Nutation und Präzession. Diese 'Nickbewegungen' des Kreisels führen dazu, dass die Erdachse schwankt und deshalb Polaris scheinbar eine Ellipse am Firmament beschreibt. Die Erdrotation und die Kenntnis von Fixpunkten ist wichtig, um zu verstehen, weshalb Gestirne untergehen können. Denn während Polaris für den Beobachter der nördlichen Hemisphäre im Prinzip ständig (auch tagsüber) beobachtbar ist, ist er für die Antipoden der südlichen Hemisphäre immer unbeobachtbar! In analoger Schlussweise hat ein Beobachter in nördlichen, gemäßigten Breiten nie das Kreuz des Südens oder die Magellanschen Wolken (Begleitgalaxien der Milchstraße) gesehen. Die Ursache besteht darin, dass die unterhalb des Horizonts liegen – das ganze Jahr über. Im intermediären Bereich gibt es Gestirne und Sternbilder, die niemals untergehen, aber um den Himmelspol rotieren. Diese Objekte sind zirkumpolar und immer oberhalb des Horizonts. Eine Sonderrolle spielt der Äquator. Hier sind alle Himmelsobjekte in Bewegung. Die Fixpunkte sind unbeobachtbar, zirkumpolare Gestirne gibt es dort nicht. Die Tageslänge variiert nicht jahreszeitlich, sondern liegt konstant bei etwa 12 Stunden. Die Dämmerung ist kurz, weil die Sonne stets senkrecht zur Horizontalebene des lokalen Äquatorialbeobachters untergeht.

Das bisher Beschriebene behandelte irdische Horizonte und damit verbundene Effekte. Es ist klar, dass diese Horizontbegriffe relativ sind, weil sie vom Standort des Beobachters auf der Erdoberfläche abhängen.

relativistische Horizonte

In der Astrophysik gibt es noch zwei Bereiche, wo Horizontbegriffe eine zentrale Rolle spielen: die relativistischeKosmologie und die Theorie Schwarzer Löcher. So unterscheidet man in der Kosmologie Teilchenhorizont und Ereignishorizont.

Teilchenhorizont

Der Teilchenhorizont kann im Rahmen der Friedmann-Weltmodelle für das Universum abgeleitet werden. Die Ausgangsfrage ist, ob man als Astronom den ganzen Kosmos überschauen kann oder der Blick nur mit endlicher Tiefe in die Weiten des Universums gelingt. Die Relativitätstheorie steckt den Rahmen ab. Gemäß dieser Theorie ist die Vakuumlichtgeschwindigkeit c von knapp 300 000 km/s das universelle Tempolimit für Teilchen und für Licht. Deshalb kann ein Astronom nur das beobachten, was seit seiner Entstehung oder Emission bis heute (bzw. bis ins lokale Universum) zu ihm gelangt ist. Der Teilchenhorizont R_H kann unter Zugrundelegung der Robertson-Walker-Metrik berechnet werden und liefert für ein flaches und strahlungsdominiertes Universum die Gleichung rechts. Darin sind c die Vakuumlichtgeschwindigkeit und H₀ die Hubble-Konstante, die ein Maß für die Expansionsgeschwindigkeit des lokalen Universums ist. Mit den aktuellen Zahlenwerten erhält man für R_H 8.3 Gpc oder 27.1 Mrd. Lichtjahre. Alles was hinter dem Teilchenhorizont liegt, also größeren Abstand als R_H hat, ist kausal entkoppelt. D.h. es kann nicht-lokale Ereignisse beeinflussen oder verursachen. Die Berücksichtigung des Teilchenhorizonts löst auch den Widerspruch im Olbers-Paradoxon auf.
Vorsicht – ein technisches Detail: Der Teilchenhorizont hängt allerdings von der jeweiligen Epoche, also von der kosmologischen Rotverschiebungz ab. Man kann auch sagen: der Teilchenhorizont ist zeitabhängig. Der Zahlenwert oben gilt nur für die strahlungsdominierte Ära. In einem sp?teren Entwicklungsstadium des Universums, z.B. der staubdominierten Phase, skaliert der Hubble-Parameter anders mit dem Skalenfaktor (oder Weltradius). Das verändert das Integral zur Berechnung des Teilchenhorizonts und führt zu einem anderen Resultat. Generell gilt: Je später die Epoche, desto größer der Teilchenhorizont. Für Einzelheiten sei das Papier von Davis & Lineweaver 2003, astro-ph/0310808, empfohlen.

kosmologischer Ereignishorizont

Der kosmologische Ereignishorizont untersucht im Prinzip die Frage, ab welchem raumzeitlichen Abstand zwei Beobachter keine Signale mehr austauschen können. Grundlage dieser Überlegung ist wieder die Robertson-Walker-Metrik. Nimmt man ein Lichtsignal an, das die Beobachter austauschen mögen, gilt für Nullgeodäten, dass das Linienelement verschwindet: ds² = 0. Bei rein zeitlichem und radialem Abstand verschwinden die Winkelanteile im Linienelement und man erhält direkt eine differenzielle Bedingung für den kosmologischen Ereignishorizont. Dies lässt sich in ein Integral umwandeln, wobei man als Grenzen die (radialen) Orte und die Epochen (Zeiten) der Beobachter nun festlegt. Es stellt sich heraus, dass ein Wert dafür in Friedmann-Universen nicht existiert. Im (unphysikalischen, da materiefreien) de-Sitter-Kosmos beträgt er gerade c/H und heißt Hubble-Radius. Im Wesentlichen ist es der Kehrwert des Hubble-Parameters.

Ereignishorizont Schwarzer Löcher

In der Theorie Schwarzer Löcher findet man ebenfalls den Begriff Ereignishorizont. Er markiert bei einem Schwarzen Loch den Bereich, ab dem nichts mehr dem Loch entkommen kann – weder Materie, noch Licht. Dieser Horizont trennt also auch Beobachtbares von Unbeobachtbarem. Aus diesem Grund ist der Blick auf die intrinsische Singularität für den neugierigen Außenbeobachter prinzipiell verwehrt. Der Mathematiker Roger Penrose nennt dies kosmische Zensur (engl. cosmic censorship) und fordert, dass sämtliche intrinsische Singularitäten von Ereignishorizonten verhüllt sein müssten. Die Beobachtbarkeit ist in praxi bereits schon weit vor dem Ereignishorizont wesentlich erschwert, dadurch dass der Rotverschiebungsfaktorg sehr klein wird. Erst am Horizont selbst wird er exakt null. Dieser Faktor geht in hoher Potenz bei jeder Emission in der Umgebung Schwarzer Löcher ein und unterdrückt deshalb schon vor dem Horizont die Strahlung. Dies zeigen Simulationen mittels Ray Tracing um rotierende Löcher (z.B. Andreas Müller, Diplomarbeit 2000, Landessternwarte Heidelberg).

Der Ereignishorizont Schwarzer Löcher hat – betrachtet man nur die Koordinaten – immer die Form einer Kugelschale. Dieser Radius schrumpft jedoch, wenn das Loch leichter ist oder wenn es rotiert. Deshalb sind Löcher vom Schwarzschild-Typ bei gleicher Masse immer größer als Löcher vom Kerr-Typ, wenn man den Ereignishorizont als Größenkriterium annimmt. Der Ereignishorizont wird auch als äußerer Horizont bezeichnet. Denn sobald ein Schwarzes Loch rotiert, bildet sich auch ein innerer Horizont aus. Diesen nennt man auch Cauchy-Horizont. Die Ringsingularität rotierender Schwarzer Löcher befindet sich immer innerhalb des Cauchy-Horizonts, nämlich immer bei r = 0; das sieht man allerdings erst in der Diskussion von Krümmungsinvarianten wie dem Kretschmann-Skalar. Im extremen Kerr-Fall maximaler Rotation (a = M in geometrisierten Einheiten) fallen beide Horizonte zusammen. In diesem Grenzfall gibt es eine nackte Singularität, die gemäß der kosmischen Zensur nach Roger Penrose verboten ist. Die Physik am Cauchy-Horizont ist sehr befremdlich: Sollte ein Beobachter jemals einer Cauchy-Fläche begegnen, erleidet er einen Strahlungstod durch eine unendliche Blauverschiebung (s.u. Chandrasekhars Buch).

Der Ereignishorizont eines Schwarzen Loches wird gerne als eine rein räumliche Hülle des Schwarzen Loches betrachtet. Das ist jedoch nur die halbe Wahrheit – wie sich im Verlauf dieses Eintrags zeigt, gibt es auch bessere Horizontbegriffe. Die Effekte Gravitationsrotverschiebung und gravitative Zeitdilatation legen noch eine andere Interpretation nahe: Das, was ein ruhender Außenbeobachter in ein Schwarzes Loch fallen sieht, wird ab einer kritischen Nähe in seiner Bewegung 'eingefroren' (engl. freezing effect). Die Ursache ist die gravitative Zeitdilatation: Zeitintervalle, in denen der Außenbeobachter etwas einfallen sieht, werden gedehnt und zwar ins Unendliche, wenn der Ereignishorizont erreicht wird. Vollkommen äquivalent ist es zu sagen, dass am Ereignishorizont die Rotverschiebung unendlich bzw. der Rotverschiebungsfaktor null wird. Das rechtfertigt andererseits zu sagen, dass der Einfall in der unendlichen Zukunft des Außenbeobachters liegt. Dieser zeitliche Aspekt des Ereignishorizontes wird gerne unterschlagen. Pointiert lässt sich sagen:

Schwarze Löcher und deren Ereignishorizonte liegen in unserer Zukunft!

neue Horizontbegriffe

Im Rahmen der Theorie Schwarzer Löcher wurden weitere Horizontbegriffe vorgeschlagen: Der absolute, der scheinbare, der isolierte, der gestreckte und der dynamische Horizont. Ihre Definitionen sind am einfachsten in direkten Gegenüberstellung zu verstehen. Chronologisch wurde zuerst der scheinbare Horizont (engl. apparent horizon) betrachtet. Er resultierte aus den ersten Betrachtungen Schwarzer Löcher und des stellaren Gravitationskollapses, vor allem unter der Führung von Roger Penrose. Der scheinbare Horizont wird definiert als die äußerste Berandungszone, wo Photonen, die dem Loch versuchen zu entkommen, gravitativ eingefangen werden. Es stellt sich heraus, dass diese Definition ein relatives Konzept, also nicht absolut ist, denn er hängt vom Bezugssystem des Beobachters ab. So wird der scheinbare Horizont für einen entfernten, ruhenden Außenbeobachter ein anderer sein, als für einen nahen, einfallenden Beobachter (FFO). Wächst das Loch durch Akkretion von Materie, so kann der scheinbare Horizont sogar von einem Ort zum anderen 'springen'.

Der absolute Horizont hingegen ist unabhängig vom Bezugssystem und wurde von Stephen Hawking eingeführt. Die Definition des absoluten Horizonts ist, dass er die Grenzfläche darstellt, die Ereignisse, die im entfernten Universum beobachtbar sind, von denjenigen Ereignissen trennt, die nicht mehr beobachtbar sind. Wie eingangs formuliert trennt er also Beobachtbares von Unbeobachtbarem. Der absolute Horizont kann kontinuierlich wachsen, wenn beispielsweise das Loch Materie aufsammelt oder mit anderen Löchern verschmilzt. Insbesondere kann der absolute Horizont nur wachsen, weil jede Energieform, die ins Loch fällt, es mit Masse anreichert und den Horizont vergrößert.

Demgegenüber bleibt der isolierte Horizont unverändert: Das Schwarze Loch ist im Gleichgewicht und wächst nicht. Das ist eine idealisierte Betrachtung, weil reale Schwarze Löcher immer mit ihrer Umgebung wechselwirken und durch Akkretion von Materie und Einfang von elektromagnetischer Strahlung und Gravitationswellen wachsen. Zu dynamischen Schwarzen Löchern fand Hawking in den frühen 1970er Jahren das Flächen-Theorem, das mit der Bekenstein-Hawking-Entropie verknüpft ist und eine Analogie zum 2. Hauptsatz der Thermodynamik aufweist.

Der absolute Horizont hat die verblüffende Eigenschaft, dass er die Kausalität verletzt! Einfallende Materie und Strahlung lassen den absoluten Horizont anwachsen, bevor sie den die Materie ihn erreicht! In Anlehnung an die Philosophie nennt man dies einen teleologischen Charakter. Die Teleologie wurde in der Philosophie vom Rationalisten Christian Wolff (1679 – 1754) eingeführt. Dort besagt dieses Prinzip, dass alle Geschehnisse auf ein bestimmtes Ziel, Telos (grch. Zweck), gerichtet sind. Es bezeichnet also eine Form von Fatalismus, einer Ergebenheit in das Schicksal: Alles hat einen Sinn und verfolgt einen bestimmten Zweck. Der absolute Horizont ist teleologisch, weil er von der Zukunft abhängt, nämlich ob Signale das entfernte (in der Zukunft liegende) Universum erreichen oder nicht. Trotz dieser seltsamen Eigenschaft, eignet sich der Begriff des absoluten Horizonts, um Entwicklungsgleichungen für das Wachstum des Horizonts eines Schwarzen Loches abzuleiten. Dies gelang Hawking und seinem Kollegen James Hartle 1972.
Der absolute Horizont weist die Schwäche auf, dass er nicht lokal und teleologisch ist. Deshalb könnte sich hier und jetzt ein Ereignishorizont ausbilden, weil in ferner Zukunft hier in der Nähe ein Gravitationskollaps stattfindet! Diese Eigenschaften sind hinderlich, wenn die Entstehung Schwarzer Löcher (beispielsweise aus dem Gravitationskollaps eines massereichen Sterns oder in der Verschmelzung zweier Neutronensterne in einem Binärsystem) auf dem Computer simuliert werden soll. Hierzu benötigt man lokale Horizontbegriffe. Diesem Kriterium genügt der dynamische Horizont, der von Abhay Ashtekar 2003 entwickelt wurde. Es handelt sich beim dynamischen Horizont um eine dreidimensionale, raumartige Mannigfaltigkeit, die in zweidimensionale Kugeln zerlegt werden kann. Dieses Verfahren ist ein 2+1 Split und verwandt mit dem ADM-Formalismus. Das Auftreten dynamischer Horizonte legt gemäß der kosmischen Zensur nahe, dass sie (oder durchaus auch mehrere) innerhalb von Ereignishorizonten liegen müssen. So weisen dynamische Horizonte auf die Existenz Schwarzer Löcher hin. Dieses Gebiet ist ein Aspekt der aktuellen Forschung in der Theorie Schwarzer Löcher.

Für Untersuchungen im Rahmen der Elektrodynamik und Magnetohydrodynamik Schwarzer Löcher eignet sich der Begriff des gestreckten Horizonts (engl. stretched horizon). Gemäß des Membran-Paradigmas wird dabei der an sich beliebig dünne Horizont zu einer Membran endlicher Dicke gedehnt. Diese Haut hat typische Eigenschaften, wie eine Spannung, einen elektrischen Widerstand (bzw. Leitfähigkeit), eine Oberflächengröße, einen Oberflächendruck, eine Entropie, eine Temperatur etc. Diese Sichtweise offenbart völlig neue Aspekte und Erklärungsmuster in der Physik Schwarzer Löcher.

Literatur

• Publikation von J. Hartle und S.W. Hawking: Energy and angular momentum flow into a black hole, Commun. Math. Phys. 27, 283-290 (1972)
• Publikation von A. Ashtekar: How black holes grow (2003), gr-qc/0306115
• Publikation von A. Ashtekar und B. Krishnan: Dynamical Horizons and their properties (2003), gr-qc/0308033
• Buch von Kip S. Thorne: Black holes and time warps: Einstein's outrageous legacy (1994), Papermac London
• Buch von S. Chandrasekhar: The Mathematical Theory of Black Holes (1983), Clarendon Press, New York