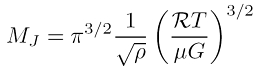Die Jeans-Masse wurde benannt nach dem englischen Physiker und Mathematiker Sir James Hopwood Jeans (1877 – 1946). Die Jeans-Masse markiert eine charakteristische Grenzmasse, oberhalb derer das Ausgangsobjekt gravitativ instabil wird und kollabieren muss.

So wird's berechnet

Rechnerisch kann man die Gleichung für die Jeans-Masse aus einer Kräftebilanz ableiten. Man geht von einer sphärisch symmetrischen Massenschale aus, die eine homogene Dichteverteilung aufweisen möge. Die Bewegungsgleichung dieser Schale enthält gerade die Gewichtskraft und den Gasdruck. Rotiert die Schale gibt es noch einen Zentrifugalterm, der ihrem Gravitationskollaps entgegenwirkt. Ist die Massenschale magnetisiert gibt es noch einen Term vom magnetischen Druck. Dieses 'magnetische Korsett' hindert die Ionen in der Schale an einer weiteren Verdichtung. Nur neutrale Teilchen bleiben unbeeinflusst vom Magnetfeld (ambipolare Diffusion).

Diskussion der Abhängigkeiten

Ohne Rotation und Magnetisierung ergibt sich die klassische Formel oben rechts. Man liest ab, dass die Jeans-Masse für

• kleinere Dichten,
• höhere Temperaturen,
• kleineres, mittleres atomares Gewicht in der Schale

ansteigt. Anschaulich ist das klar, weil eine heißere Ansammlung von Material einen höheren Gasdruck aufweist, der dem Kollaps entgegen gerichtet ist. Ebenso sind dünnere Materiewolken schwieriger zu kollabieren. Sind die Spezies in der Schale leichter (viel Wasserstoff und Helium, statt Kohlenstoff und Sauerstoff) gilt dasselbe.

Hier braucht man's

Der wichtige Anwendungsbereich der Jeans-Masse findet sich in der Theorie der Sternentstehung, wenn untersucht wird, ab welchen Massen Gaswolken des interstellaren Mediums (ISM) zu Protosternen und YSOs kollabieren können.