Die Kepler-Gesetze sind benannt nach dem deutschen Astronom Johannes Kepler (1571 – 1630), der die Planetendaten seines dänischen Kollegen und Zeitgenossen Tycho Brahe (1546 – 1601) auswertete. Damals wurde einfache optische Linsenteleskope zur astronomischen Beobachtung verwendet, die dem Prototyp, den der Holländer Hans Lipperhey (1570 – 1619) erfand und den Galileo Galilei (1564 – 1642) weiterentwickelte, sehr ähnlich waren. Diese kleinen Fernrohre dienten vor allem der Mond- und Planetenbeobachtung.

Keplers Verdienste

Kepler hatte drei Gesetze der Himmelsmechanik rein empirisch gefunden. Eine theoretische Herleitung dieser später Kepler-Gesetze genannten Gesetze wurde mit der Newtonschen Gravitationstheorie möglich. Im Physikstudium sind die Keplerschen Gesetze auch heute noch Pflichtübung in der klassischen Mechanik.
Die drei Gesetze lauten:

• (1) Die Planetenbahnen sind Ellipsen, in dessen einem Brennpunkt die Sonne steht.
• (2) Die Verbindungslinie Planet – Sonne (Fahrstrahl) überstreicht in gleichen Zeitintervallen gleich große Flächen.
• (3) Die Quadrate der Umlaufzeiten der Planeten verhalten sich wie die Kuben der großen Halbachse der Ellipse ihrer jeweiligen Bahn.

Himmelsbahnen sind Kegelschnitte

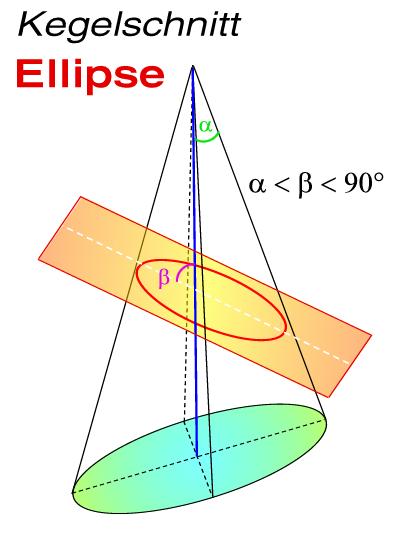In dieser historischen Form wurden die Kepler-Gesetze an den Planeten im Sonnensystem beobachtet und bewiesen. Vom physikalischen Standpunkt haben sie jedoch eine viel allgemeinere Gültigkeit und astronomisch einen weit größeren Anwendungsbereich. Es handelt sich beim Kepler-Problem um die Bewegung einer Masse m in einem gravitativen Zentralpotential, nämlich demjenigen, das von der Zentralmasse M gebildet wird. Eine mathematische Analyse des Problems zeigt, dass alle Bahnen von Himmelskörpern im Sonnensystem Kegelschnitte sind. Das heißt die Bahnformen ergeben sich als Schnittfiguren, wenn man einen Kreiskegel mit einer Ebene schneidet. Diese Figuren sind alle bekannt und heißen Kreis, Ellipse, Parabel und Hyperbel – sie unterscheiden sich in der Exzentrizität. Die Ellipse ist dabei einer der wichtigsten Kegelschnitte, beschreibt sie doch die Planetenbahnen im Sonnensystem. Wie diese Schnittfigur zustande kommt, zeigt die Abbildung rechts. Die Ellipse ist dabei ein Sonderfall, der sich nur ergibt, wenn der halbe Öffnungswinkel des Kegels α und der Winkel der Ebene mit der Kegelachse β die Bedingung oben rechts erfüllen; bei anderen Winkelbedingungen ergeben sich entsprechend Kreis, Parabel und Hyperbel.

weit reichende Bedeutung für die Physik

Die Kepler-Gesetze bestimmen nicht nur die Dynamik im Sonnensystem, sie lassen sich auf viele andere astronomische Systeme übertragen: Doppelsternsysteme oder sogar auf Sterne, die um ein Schwarzes Loch kreisen. Das dritte Kepler-Gesetz kann als Relation zwischen Umlaufzeit (bzw. Umlauffrequenz) und Zentralmasse formuliert werden. In dieser Form wird es exzessiv in zahlreichen kosmischen Systemen genutzt, um Massen kinematisch zu bestimmen. Ein prominentes und aufregendes Beispiel ist das Zentrum der Milchstraße: aus der Dynamik von Sternen und von Gas folgt eine gigantische, konzentrierte Masse, die dunkel im Galaktischen Zentrum lauert. Die beste Interpretation, die Astronomen für dieses seltsame Gebilde haben, ist, dass sich hier ein supermassereiches Schwarzes Loches von gut drei Millionen Sonnenmassen befindet. Damit die entsprechenden Bahnberechnungen bei Schwarzen Löchern noch ihre Gültigkeit haben, müssen die klassischen Kepler-Gesetze relativistisch verallgemeinert werden. Das ist allerdings möglich.

Einschränkungen & Erweiterungen

Es seien noch einige Einschränkungen bzw. Erweiterungen der Kepler-Gesetze angemerkt: die Bewegung eines Objekts um das andere (Zweikörperproblem) erfolgt um den gemeinsamen Schwerpunkt. Im Falle des Systems Planet – Sonne liegt dieser aufgrund der enormen Masse der Sonne im Vergleich zu den Planeten nahe bei der Sonne.
Das zweite Kepler-Gesetz beruht physikalisch auf der Erhaltung des Drehimpulses, was wiederum mit der Achsensymmetrie des Problems zusammenhängt (Noether-Theorem, siehe auch Symmetrie). Dieser Erhaltungssatz ist auch der Grund dafür, dass die (Planeten-)Bewegung in einer Ebene stattfindet (vergleiche auch eine weitere Erhaltungsgröße, der Runge-Lenz-Vektor). Die Kepler-Gesetze vernachlässigen kleine Beiträge von den gravitativen Wechselwirkungen der Planeten untereinander. Im Allgemeinen ist nur das Zweikörperproblem exakt lösbar. Schon bei nur einem weiteren Körper, dem Dreikörperproblem, ist eine Lösung nur noch approximativ numerisch zu finden. Im restringierten Dreikörperproblem ist eine der drei Massen viel leichter, was die Lösung erleichtert.

Web-Artikel

• Das größte Schwarze Loch der Milchstraße