Die Kerr-de-Sitter-Lösung ist eine Lösung der Einsteinschen Feldgleichungen der Allgemeinen Relativitätstheorie mit Λ-Term (siehe kosmologische Konstante). Physikalisch motiviert ist diese Raumzeit, wenn man ein rotierendes Schwarzes Loch beschreiben will, das sich in einer Umgebung befindet, die mit dem Λ-Fluidum angefüllt ist.

zum Namen

Der Name Kerr-de-Sitter-Lösung kommt daher, weil diese Metrik beides beinhaltet: die rotierende Eigenschaft von der Kerr-Lösung und die kosmologische Konstante wie in der de-Sitter-Lösung.

Eigenschaften: Masse, Rotation, Λ

Die Kerr-de-Sitter-Raumzeit ist eine Drei-Parameter-Lösung, weil Massenparameter M, spezifischer Drehimpuls a = J/Mc und die kosmologische Konstante Λ die Eigenschaften der Metrik eindeutig festlegen.

Unterscheidung nach Vorzeichen von Λ

Wie bei der de-Sitter-Raumzeit auch, sprechen Theoretiker von der Kerr-de-Sitter-Lösung (KdS-Metrik), falls Λ > 0 (repulsive kosmologische Konstante; Antigravitation) und von der Kerr-Anti-de-Sitter-Lösung (KAdS-Metrik), falls Λ < 0 (attraktive kosmologische Konstante). Im Grenzfall Λ = 0 ist gerade die gewöhnliche Kerr-Metrik mit verschwindender kosmologischer Konstante realisiert.
Interessanterweise hat die KAdS-Metrik keinen Ereignishorizont.

Linienelement

Der Vollständigkeit halber sei das Linienelement an dieser Stelle notiert:

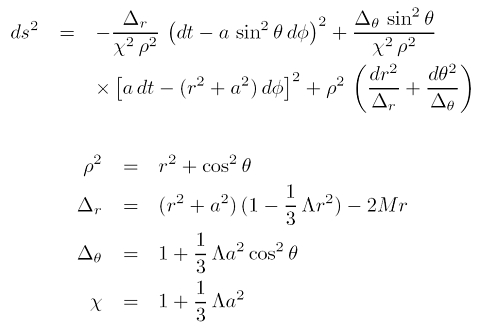
Weitere Raumzeiten

Verschwindet der Drehimpuls des Loches, so ist gerade die Schwarzschild-de-Sitter-Lösung realisiert. Gibt es eine zusätzliche elektrische Ladung in der KdS-Metrik, so heißt die Raumzeit Kerr-Newman-de-Sitter-Lösung

Publikationen zum Thema

• Gibbons, G.W. & Hawking, S.W.: Cosmological event horizons, thermodynamics, and particle creation, Phys. Rev. D15, 2738, 1977
• Stuchlik, Z. & Calvani, M.: Null geodesics in black hole metrics with non-zero cosmological constant, Gen. Rel. Grav. 23, 507, 1991