Die Kerr-Lösung ist eine Vakuum-Lösung der Einsteinschen Feldgleichungen und beschreibt die Metrik rotierender, nicht geladener Schwarzer Löcher. Allgemeiner gesprochen beschreibt es den gekrümmten Außenraum einer elektrisch neutralen, rotierenden Masse. In guter Näherung können mit der Kerr-Lösung rotierende Massen auf der Basis der Allgemeinen Relativitätstheorie beschrieben werden.

Ein Rechenkunststück

Der Neuseeländer Roy Patrick Kerr fand diese Lösung 1963 in kartesischen Koordinaten, was als mathematische Meisterleistung gewertet werden muss. Denn einerseits ist es generell schwierig, exakte Lösung der komplizierten Einsteinschen Feldgleichungen zu finden und andererseits hat die Kerr-Lösung in den kartesischen Koordinaten eine recht komplizierte Struktur. Durch Koordinaten, die besser an die Symmetrie der Kerr-Geometrie angepasst sind, wird auch ihre mathematische Formulierung einfacher. Üblicherweise notiert man die Kerr-Geometrie in pseudosphärischen Boyer-Lindquist-Koordinaten. Das Linienelement lautet dann:

Alternativ kann es auch in Matrixform aufgeschrieben werden, d.h. der metrische Tensor der Kerr-Metrik in Boyer-Lindquist-Form. Die im Linienelement enthaltenen Funktionen sind unter dem Eintrag Boyer-Lindquist-Koordinaten ausführlich notiert.

Rotation erschwert die Sache

Prinzipiell kann gesagt werden, dass rotierende Schwarze Löcher deutlich komplexere Raumzeiten sind, als ihr nicht rotierendes Pendant, die Schwarzschild-Lösung. Denn die Raumzeit rotiert. Dies spiegelt sich tensoriell darin wider, dass der metrische Tensor nicht mehr diagonal ist: es gibt in Boyer-Lindquist-Koordinaten einen Kreuzterm, der azimutale und zeitliche Komponente koppelt. In den ebenfalls pseudosphärischen Kerr-Schild-Koordinaten gibt es sogar drei Kreuzterme! Das ist zwar eine zusätzliche Komplexität, aber in numerischen Simulationen von rotierenden Löchern kann die Verwendung von Kerr-Schild-Koordinaten zweckmäßiger sein, weil dann Randbedingungen (in Hydrodynamik und Magnetohydrodynamik) besser umgesetzt werden können.

zwei Eigenschaften: Masse und Drehimpuls

Kerr-Löcher haben also die physikalischen Eigenschaften MasseM und DrehimpulsJ. Das Robinson-Theorem diktiert, dass Raumzeiten mit bestimmten Voraussetzungen notwendigerweise identisch mit der Kerr-Lösung sein müssen. Die Rotation kann durch den so genannten Kerr-Parameter (Rotations- oder Spinparameter) a charakterisiert werden. Diese Zahl ist physikalisch gesprochen ein spezifischer Drehimpuls a = J/Mc. In geometrisierte Einheiten (G = c = 1) variiert a zwischen den Werten -M (maximale retrograde Rotation) und +M (maximale prograde Rotation). Manchmal setzen Theoretiker aus Bequemlichkeit auch M = 1 (bisweilen auch auf meiner Website), so dass a zwischen -1 und 1 variiert. Die Maximalwerte +1 und -1 sind mit Vorsicht zu genießen, denn die Singularität der Kerr-Lösung wird dann nach außen hin sichtbar! Der Relativist Kip Thorne hat 1974 herausgefunden, dass die Rotation einen kritischen Maximalwert hat, nämlich a = 0.998M. Gilt exakt a = 0, so geht die Kerr-Lösung in die statische Schwarzschild-Lösung über.

gekrümmte Raumzeit

Schwarze Löcher sind Raumzeiten, die sehr starke Krümmungen aufweisen, vor allem wenn man in die Nähe der Krümmungssingularität kommt. Nach außen nimmt die Krümmung allerdings rapide ab und verschwindet sogar im Grenzfall einer unendlich hohen Entfernung zum Loch. Diese Eigenschaft haben sowohl Schwarzschild-Metrik, als auch Kerr-Metrik, und sie heißt asymptotische Flachheit. D.h. für sehr große Abstände vom Schwarzen Loch gehen die Schwarzschild- bzw. Kerr-Metrik in die Minkowski-Metrik über.

Eigenschaften der Kerr-Lösung

• Es gibt zwei Horizonte, einen inneren Horizont oder Cauchy-Horizont bei r^-_H und einen äußeren Horizont bei r⁺_H. Letztgenannter ist der eigentliche Ereignishorizont, weil er festlegt, ab welchem Abstand ein rotierendes Loch für einen Außenbeobachter völlig schwarz erscheint.
  Beide Horizonte hängen nur von der Masse und dem Drehimpuls des Loches ab (siehe erste Gleichung unten)! Die Horizonte sind so genannte Nullflächen und werden von den beiden Killing-Vektoren der Kerr-Geometrie aufgespannt.
• Um die Horizonte herum gibt es eine Ergosphäre, d.h. eine Region, wo die Rotation der Raumzeit sehr stark wird. Alles, was sich lokal in der Ergosphäre befindet (Sterne, Akkretionsscheiben, Beobachter, Licht!), wird von der rotierenden Raumzeit mitgezogen. Dieses Phänomen heißt Frame-Drag. Innerhalb der Ergosphäre kann insbesondere kein Beobachter mehr statisch sein und muss rotieren. Die Struktur der rotierenden Raumzeit zwingt einfach alles, Materie und Strahlung, mit ihm zu rotieren! Am äußeren Horizont dreht sich alles mit der Winkelgeschwindigkeit des Loches (Anmerkung: In der Schwarzschild-Metrik fehlt zwar die Ergosphäre, doch gibt es hier eine Art Anti-Frame-Drag: alles muss statisch sein!) Aus diesen Gründen heißt die Ergosphäre auch statisches Limit, r_stat. Mathematisch ist die Ergosphäre definiert durch das Verschwinden der zeitartigen Komponente (00-Komponente) des metrischen Tensors. Demnach ist die Ergosphäre eine Fläche unendlicher Rotverschiebung bzw. verschwindenden Rotverschiebungsfaktors. Die Ergosphäre ist im Gegensatz zu den Horizonten abgeplattet – mathematisch ist das zu sehen an der Abhängigkeit vom Polarwinkel θ in der zweiten Gleichung unten.
• Wie alle klassischen Schwarzen Löcher hat auch die Kerr-Lösung eine intrinsische Singularität (Krümmungssingularität, Raumzeit-Singularität). Sie folgt aus einer Diskussion des Riemann-Tensors der Kerr-Metrik, insbesondere der Riemannschen Invarianten wie dem Kretschmann-Skalar. In Boyer-Lindquist-Koordinaten notiert, muss die Funktion ρ ('rho') verschwinden. Sie taucht im Nenner der Invarianten auf. Wird sie null, wird die Krümmung unendlich. Für die Funktion ρ gilt: ρ² = r²+a²cos²θ. Eine Diskussion dieses Ausdrucks (am besten mit Kerrs historischen kartesischen Koordinaten) führt auf das erstaunliche Resultat, dass die Kerr-Lösung im Zentrum eine Ringsingularität besitzt. Diese Ringsingularität befindet sich immer in der Äquatorebene des Lochs, innerhalb des Cauchy-Horizonts und im Zentrum des Loches bei r = 0, wie die Krümmungsinvarianten belegen. Der ringförmige Massenstrom ist die Quelle der achsensymmetrischen Gravitation der Kerr-Geometrie – sonst gibt es in der Vakuumraumzeit keine Quellen.

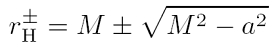
Schema mit struktureller Information

Häufig sind diese genannten Eigenschaften der Kerr-Lösung in Abbildungen wie dieser zusammengefasst:

Solche Bilder sind jedoch aus einer Reihe von Gründen mit Vorsicht zu genießen: Der Betrachter kann dazu verleitet werden zu glauben, dass genau so ein Schwarzes Loch aussieht. Ein Schwarzes Loch ist aber ein schwarzes Objekt. Ein Außenbeobachter kann aufgrund der Gravitationsrotverschiebung nie etwas vom Inneren des Loches, z.B. die Singularität, sehen. Ein anderes Problem ist, dass die Abbildung oben nicht auf Invarianten beruht, d.h. sie geht auf die Verwendung eines speziellen Koordinatensystems zurück. In einem anderen sieht es anders aus! Nur geeignete Invarianten der ART, wie die gerade angesprochenen Krümmungsinvarianten, erlauben ein objektives Bild. Die Abbildung oben kann also nur dazu dienen, einen Überblick über die strukturellen Komponenten eines Lochs zu bekommen.

Realistischer Eindruck vom Anblick eines Schwarzen Loches

Ist man daran interessiert, wie sich der visuelle Eindruck eines Loches für einen entfernten Beobachter gestaltet, so muss man eine Simulationstechnik namens relativistisches Ray Tracing betreiben. Die simulierten Bilder sehen aus, wie das folgende:

Das rotierende Schwarze Loch befindet sich in der Bildmitte. Es tritt nur deshalb in Erscheinung, weil seine Umgebung leuchtet. Denn um das Schwarze Loch befindet sich eine ebenfalls (hier gegen den Uhrzeigersinn) rotierende Standardscheibe – eine dünne Materiescheibe, die Strahlung abgibt. Der helle Fleck links vom Loch ist auf Blauverschiebung der Strahlung der sich nähernden Scheibenseite zurückzuführen. Entsprechend ist die rechte sich entfernende Seite rotverschoben. Es handelt sich um eine relativistische Verallgemeinerung des Doppler-Effekts.
Die Dunkelheit um und die Schwärze am Loch ist durch einen Effekt namens Gravitationsrotverschiebung begründet. So sieht ein Schwarzes Loch aus!

Horizonte

Bei maximaler Rotation (a = M) sind beide Horizonte bei einem Gravitationsradius. Bei verschwindender Rotation hingegen (a = 0), was der Schwarzschild-Lösung entspricht, ist der äußere Horizont bei zwei Gravitationsradien oder einem Schwarzschildradius. Der innere Horizont koinzidiert mit der zentralen Schwarzschild-Singularität bei r = 0.

innere Kerr-Lösung?

Alle Versuche, eine innere Kerr-Lösung zu finden sind bisher gescheitert. Bei der Schwarzschild-Lösung ist dies allerdings möglich (siehe Eintrag Schwarzschild-Lösung).

Geodäten

Innerhalb des Horizonts treten raumartige Geodäten (wie bei den Tachyonen) auf, die die Kausalität verletzen! Da jedoch nichts davon nach außen dringen kann (geschlossene Geodäten), erfüllt diese Kausalitätsverletzung gewissermaßen die kosmische Zensur: Wie die Singularität sind sie durch den Ereignishorizont verhüllt.
Die Geodätengleichung der Kerr-Metrik ist mithilfe der Carter-Konstante vollständig integrabel. Mit dieser Standardmethode werden numerisch Teilchenbahnen und Trajektorien des Lichtes in der Kerr-Metrik studiert. Damit kann man relativistisches Ray-Tracing betreiben und viele Bilder erzeugen, die zeigen wie rotierende Schwarze Löcher, optisch die Umgebung verzerren. In der Astrophysik nutzt man diese Methode, um relativistische Spektren wie die relativistisch verbreiterte Eisenlinie zu simulieren und mit Beobachtungsdaten zu vergleichen.
Eine andere wichtige Anwendung der Kerr-Lösung in der Astrophysik ist die Beschreibung hydrodynamischer und magnetohydrodynamischer Phänomene auf dem Hintergrund der Kerr-Raumzeit (siehe auch Akkretion).

Aspekte zur Stabilität

Ein wichtiges Kriterium für Lösungen der Einsteinschen Feldgleichungen ist deren Stabilität. Die Theoretiker untersuchen in einer Stabilitätsanalyse der Metrik, wie sie sich unter kleinen Störungen verhält: Schwingt die gestörte Metrik in die ursprüngliche Lösung zurück? Falls ja, ist die Raumzeit stabil. Die Schwarzschild-Lösung ist der Grundzustand der relativistischen Gravitation (in vielen Details nachzulesen im Buch von S. Chandrasekhar mit dem Titel The Mathematical Theory of Black Holes). Demgegenüber ist die Kerr-Lösung zwar stabil gegen axialsymmetrische Störungen. Man kann aber durch Penrose-Prozesse oder Blandford-Znajek-Mechanismen, die beide in der Ergosphäre stattfinden, die Rotationsenergie theoretisch sogar vollständig extrahieren, so dass aus dem Kerr- ein Schwarzschild-Loch wird. In diesem Sinne ist die Kerr-Metrik weniger stabil.

dicker Web-Artikel

• Schwarze Löcher – Das dunkelste Geheimnis der Gravitation, darin speziell das Kapitel zur Kerr-Lösung.