Die kovariante Ableitung ist eine der wesentlichen Differentialoperationen, die man auf Tensoren in der Allgemeinen Relativitätstheorie (ART) anwendet. Daneben gibt es die partielle Ableitung, absolute Ableitung und die Lie-Ableitung.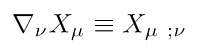
Die kovariante Ableitung weist in ihrer Grunddefinition Ähnlichkeiten zum Differenzen- bzw. Differentialquotienten der Analysis einer Veränderlichen auf. Anschaulich kann die kovariante Ableitung als ein Vergleich zweier parallel transportierter Tensoren verstanden werden.
Ihren Namenszusatz kovariant verdankt sie der Tatsache, dass ein Tensor vom 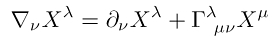Typus (i,j) eine weitere kovariante Stufe erhält und so zum Typus (i, j+1) wird.
Allgemein und etwas salopp gesprochen ist die kovariante Ableitung eines Tensors beliebiger Stufe eine Summe aus dessen partieller Ableitung plus einer Anzahl weiterer Terme, deren Anzahl der Stufenhöhe entspricht, die mit dem Christoffel-Symbol gewichtet sind. Dabei haben diese Terme positives Vorzeichen, wenn sie sich auf einen kontravarianten Index des Tensors beziehen und bei den kovarianten Indizes ein negatives Vorzeichen.
Die kovariante Ableitung eines Tensors 0. Stufe, eines Skalars, geht in seine partielle Ableitung über (kein weiterer Term mit Christoffel-Symbol), die kovarianten Ableitungen von Vektoren (Tensoren 1. Stufe) enthalten neben der partiellen Ableitung einen Term mit Christoffel-Symbol.
Die üblichen Schreibweisen für die kovariante Ableitung sind die mit Nabla-Operator ∇, der als Index die Koordinate hat, nach der abgeleitet wird oder mit Semikolon und angefügtem Ableitungsindex.
Ein gemischter Tensor zweiter Stufe (ein Index kovariant, ein Index kontravariant) wird folgendermaßen kovariant abgeleitet:

Die Gleichungen der Speziellen Relativitätstheorie (SRT) enthalten vielfach partielle Ableitungen. In der Regel kann man formal den Übergang zur ART vollziehen, indem man die partiellen durch kovariante Ableitungen ersetzt. Anhand der Definition der kovarianten Ableitung (siehe oben) wird klar, warum das so ist: die kovariante Ableitung enthält neben der partiellen Ableitung (erster Term) einen weiteren Term, der von den Christoffel-Symbolen ('Ableitungen der Metrik') abhängt. In der SRT, die auf einer flachen Raumzeit, der Minkowski-Metrik, basiert, verschwinden gerade diese Christoffel-Symbole, denn die Ableitung einer Konstante ist null.