Der Kretschmann-Skalar ist eine wichtige Größe in der Allgemeinen Relativitätstheorie (ART), um die Krümmung von Raumzeiten darzustellen.

Masse macht krumme Sachen

Krümmung wird durch Energien hervorgerufen. So lautet eine fundamentale Aussage der ART, dass Massen die Raumzeit krümmen. Die Krümmung variiert im Allgemeinen über die Raumzeit und unterscheidet sich von Ort zu Ort – von Koordinate zu Koordinate. Krümmung kann sogar unendlich werden – genau das passiert in den Krümmungssingularitäten oder echten Singularitäten der ART. Der Kretschmann-Skalar eignet sich nun besonders gut, um die Singularitäten einer gegebenen Raumzeit oder Metrik zu finden.

Krümmungsinvarianten: frei von Koordinatenwahl

Der Kretschmann-Skalar wird alternativ auch als Riemannsche Invariante bezeichnet. Der erste Wortbestandteil Riemann bezieht sich darauf, dass diese Größe aus dem Riemann-Tensor (Krümmungstensor) hervorgeht, der in der ART gerade die Krümmung mathematisch beschreibt. Der zweite Wordbestandteil Invariante ist darauf zurückzuführen, dass die Größe unabhängig von verwendeten Koordinaten ist. Das ist eine hervorragende Eigenschaft einer mathematischen Größe, die den Physikern besonders gefällt! Denn es reicht die einmalige Berechnung in irgendeinem Koordinatensystem damit sehr generelle Aussagen gemacht werden können.
Ganz allgemein kann man sagen, dass die Riemannsche Invariante eine Summe aus Weylscher Invariante und den Ricci-Invarianten ist. Liegen entsprechend Weyl-Tensor (C), Ricci-Tensor (R mit zwei Indizes) und Ricci-Skalar (Skript R ohne Index) vor, so folgt die Riemannsche Invariante gemäß:

Die Berechnungen der Riemannschen Invarianten einer vorgegebenen Metrik sind schon bei einfachen Raumzeiten mit hoher Symmetrie relativ aufwendig. Die Mühe lohnt allerdings, weil mit dem Resultat die Krümmungseigenschaften ganz allgemein diskutiert werden können. Die Relativisten sind ebenso an den Krümmungssingularitäten besonders interessiert. Man findet sie, indem man divergentes Verhalten der Riemannschen Invarianten untersucht, also Koordinaten bestimmt, wo die Invariante unendlich wird.

Kretschmann für Kerr

Im Folgenden wird als Beispiel der Kretschmann-Skalar der Kerr-Geometrie diskutiert. Die Kerr-Metrik ist wichtig für die Astronomie, weil sie relativistisch rotierende, elektrisch ungeladene Schwarze Löcher beschreibt. Die Gleichung für den Kretschmann-Skalar ist im Lexikoneintrag Riemann-Tensor dargestellt. Das Loch möge sehr schnell rotieren und einen Drehimpulsparameter a/M von 0.998 haben. Seine Masse wird ohne Beschränkung der Allgemeinheit gleich 1 gesetzt (die Masse skaliert nur den Radius). Visualisiert man nun die Invariante als Maß für die Krümmung in Abhängigkeit von den Koordinaten Radius (in Einheiten des Gravitationsradius) und Poloidalwinkel (θ, im Bogenmaß), so ergibt sich folgendes Bild (basierend auf R.C. Henry, ApJ 535, 350, 2000):

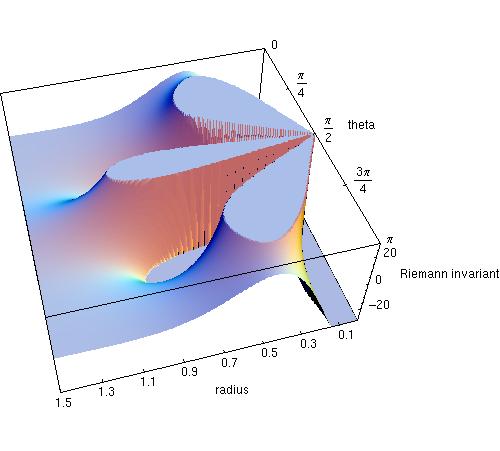
Bei großen Radien verschwindet die Krümmung nahezu. Diese Eigenschaft ist die asymptotische Flachheit der Kerr-Metrik. Mit Annäherung an das Loch nimmt die Krümmung stark zu. Weiterhin fällt auf, dass sich der linke und rechte Teil des Reliefs gleichen – das ist nichts anderes als die Achsensymmetrie der Metrik rotierender Schwarzer Löcher. Die Spiegelebene in der Mitte des Bildes ist gerade die Äquatorialebene des Loches. Die Krümmung nimmt wie man anhand der vertikalen Skala sieht rapide zum Innern des Loches hin zu. Dies geschieht allerdings nicht räumlich homogen, sondern es gibt eine starke Abhängigkeit vom Poloidalwinkel ('Breitengrad'): Erstaunlicherweise erkennt man nicht nur drei herausragende 'Gipfel' (positive Krümmung), sondern auch zwei 'tiefe Täler', die ins Bodenlose fallen. In den Senken liegt eine negative Krümmung vor, die vollkommen wesensverschieden von negativ gekrümmten Sattelflächen ist (Henry 2000). Die negative Krümmung wird auch an den Polen des Lochs besonders groß. Wie das und negative Krümmung überhaupt zu interpretieren sind, ist bislang unklar.

Jagd auf Krümmungssingularitäten

Es lohnt sich, die Orte verschwindender Krümmung zu diskutieren: Eine Analyse der Konturlinien für Krümmung null zeigt, dass sie interessanterweise in der Äquatorialebene bei Radius null konvergieren. In der Krümmungssingularität muss der Kretschmann-Skalar gegen unendlich gehen. Ein solches Verhalten zeigen die drei Gipfel die zu kleinen Radien hin verschmelzen und divergieren. Dieses Verhalten weist auf die Ringsingularität der Kerr-Geometrie hin.