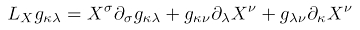Die Lie-Ableitung ist eine spezielle, mathematische Operation, die bei der Allgemeinen Relativitätstheorie eine Rolle spielt. Die Relativitätstheoretiker sind an den Symmetrieeigenschaften von Raumzeiten interessiert. Sie betrachten daher Isometrien. Es stellt sich heraus, dass ein mathematischer Ausdruck, die so genannte Lie-Ableitung der Metrik verschwinden muss, um die Metrik über eine Koordinatentransformation auf sich selbst abzubilden. Diese Gleichung heißt dann Killing-Gleichung und deren Lösungen Killing-Felder.

Was passiert bei der Lie-Ableitung?

Anschaulich entspricht die Lie-Ableitung einem Paralleltransport eines Tensors von einem Punkt an einen anderen in der Raumzeit entlang einer Kongruenzkurve. Danach werden die Tensoren an den verschiedenen Punkten verglichen. Beim Grenzübergang der Ableitung wird der Abstand infinitesimal, d.h. beliebig klein.

Eigenschaften der Lie-Ableitung bezüglich eines Vektorfelds

• Linearität
• Erfüllung der Leibniz-Regel (Produktregel bei Differentiation)
• Erhaltung des Tensortyps
• Kommutativität (Vertauschung) mit der Verjüngung
• Anwendbarkeit auf alle Tensoren