Die Metrik ist in Einsteins Relativitätstheorie ein geometrisches Gebilde, das von den drei Raumdimensionen und der Zeitdimension aufgespannt wird. Diese vierdimensionale Mannigfaltigkeit wird auch Raum-Zeit-Kontinuum oder kurz Raumzeit (engl. space-time) genannt.
Raum und Zeit bilden eine Einheit und stellen die 'Bühne (die Welt), wo sich die Geschehnisse ereignen. Diese 'Bühne; ist jedoch dynamisch (siehe auch Diffeomorphismus) und in ihrer Dynamik beeinflusst von jeder Energieform, z.B. von der Masse.
In Einsteins Theorie ist die Metrik ein Tensor. Dieser metrische Tensor ist symmetrisch und besteht deshalb aus (im Allgemeinen) zehn unabhängigen Komponenten. Wegen der vier Dimensionen kann der metrische Tensor als 4 × 4-Matrix geschrieben werden, der eigentlich 4 × 4 = 16 Komponenten hat. Die Symmetrie reduziert die 16 auf zehn unabhängige Komponenten.
Im Prinzip kann man die Begriffe Raumzeit, Metrik, metrischer Tensor und Linienelement synonym verwenden. Das Linienelement stellt die Metrik kompakt als eine Gleichung dar.

flache Metrik

Der einfachste metrische Tensor ist derjenige einer flachen Raumzeit, die so genannte Minkowski-Metrik. In Abwesenheit von Massen und Energie oder bei verschwindend kleinen Energien liegt diese Vakuum-Raumzeit vor, die auch den Hintergrund der Speziellen Relativitätstheorie bildet. Der Minkowski-Tensor ist deshalb sogar diagonal, hat nur vier von null verschiedenen Komponenten auf der Matrixdiagonalen. Diese sind sogar konstant, was in eine ungekrümmte und statische Raumzeit mündet. Die Zeit zeichnet sich gegenüber den Raumkoordinaten dadurch aus, dass sie entgegengesetztes Vorzeichen trägt. Dieser Umstand sichert die Lorentzinvarianz des Linienelements. D.h. verschiedene Beobachter in unterschiedlichen Bezugssystemen mögen unterschiedliche Zeitabstände oder Raumabstände für sich genommen messen, aber raumzeitliche Abstände stimmen überein und sind in diesem Sinne absolut. Die Relativisten sagen auch: das Linienelement ist eine Invariante.

Signatur der Metrik

Es gibt genau zwei mögliche Konventionen für die Vorzeichenwahl in der Minkowski-Metrik: (- + + +) oder (+ – - -). Dies nennt man die Signatur der Metrik. Kurz sagt man auch, die Signatur sei +2 oder -2, entsprechend der Summe der Vorzeichen.
Diese Freiheit bei den Vorzeichen gilt für alle Metriken der Relativitätstheorie. Im Vorzeichenunterschied schlägt sich letztendlich die unterschiedliche Natur von Raum und Zeit nieder: Die drei Raumdimensionen haben alle das gleiche Vorzeichen, entweder + + + oder – - -; legt man diese Vorzeichen fest, so muss die Zeit das entsprechend gegensätzliche Vorzeichen haben. Raum und Zeit bilden zwar ein Kontinuum, doch ihr unterschiedliches Wesen besteht einzig in diesem scheinbar harmlosen Vorzeichenunterschied.

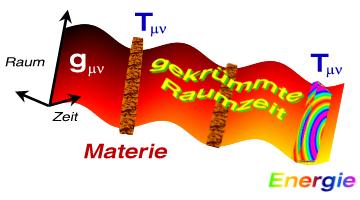
gekrümmte Metrik

Die Morphologie der vierdimensionalen Mannigfaltigkeit ändert sich entscheidend, wenn Quellen des Gravitationsfeldes auftauchen. Das illustriert die Abbildung oben. Der metrische Tensor einer gekrümmten Metrik enthält Komponenten, die koordinatenabhängig sind. Sie legen gerade die Krümmungseigenschaften der betreffenden Metrik fest.

Beispiel 1: die gekrümmte Schwarzschild-Metrik

Die historisch erste Lösung einer daraus resultierenden gekrümmten Raumzeit war die Schwarzschild-Metrik (1916). Sie beschreibt kugelsymmetrische und statische Raumzeiten von Punktmassen und wird in der Astrophysik auf relativistische, aber nicht rotierende Sterne und insbesondere auf statische, nicht rotierende Schwarze Löcher angewendet. Die Schwarzschild-Lösung ist eine Vakuumlösung der Einsteinschen Feldgleichungen, der Energie-Impuls-Tensor ist null, aber die Quelle der Gravitation ist eine punktförmige Singularität im Symmetriezentrum der Raumzeit.
Der zugehörige metrische Tensor der Schwarzschild-Lösung ist ebenfalls diagonal wie die Minkowski-Metrik, aber die Diagonalelemente sind koordinatenabhängig. Daraus folgen die Krümmungseigenschaften der Schwarzschild-Raumzeit fest, die vor allem nahe der Singularität wesentlich werden.

Beispiel 2: die gekrümmte Kerr-Metrik

Eine rotierende Verallgemeinerung der statischen Schwarzschild-Lösung wurde erst 1963 von dem neuseeländischen Mathematiker Roy Patrick Kerr gefunden, die seither Kerr-Metrik heißt. Bei dieser Metrik sind auch zwei Nebendiagonalelemente (die tΦ-Komponente und ihr symmetrisches Pendant) von null verschieden, in denen sich gerade die Rotation der Raumzeit widerspiegelt (siehe auch Lense-Thirring-Effekt).

Symmetrien der Raumzeit

Transformationen, die die Metrik in ihrer Gestalt nicht verändern, also forminvarinat lassen, nennt man Isometrien. Die Isometriebedingung führt auf die Killing-Gleichung und liefert die Killing-Felder einer Metrik, die eng mit deren Symmetrie zusammenhängen. Dies ist ein wichtiges Werkzeug, um die Symmetrieeigenschaften von Raumzeiten zu studieren.

Determinante der Metrik

Eine wichtige Größe, die man aus dem metrischen Tensor ableitet, ist die Determinante der Metrik, üblicherweise mit g bezeichnet. Stellt man den metrischen Tensor als 4 × 4-Matrix dar, folgt die Determinante nach den üblichen Regeln der Matrizenrechnung.
g geht zum Beispiel in die Lagrangedichte der ART ein (Einstein-Lagrangedichte, Einstein-Hilbert-Wirkung) und kann Ausgangpunkt einer Quantenfeldtheorie der Gravitation genutzt werden. In den Eichtheorien ist das eine mächtiger, mathematischer Apparat.

Metriken der Kosmologie

Die zentrale Metrik der Kosmologie ist die Robertson-Walker-Metrik, die der Schwarzschild-Metrik sehr ähnelt. Allerdings ist in dieser relativistischen Beschreibung des materiegefüllten Universums neu, dass die Friedmann-Weltmodellekeine Vakuumraumzeiten sind. Dann wird der Energie-Impuls-Tensor verschieden von null und die Materie im vorliegenden Fall durch eine ideale Flüssigkeit beschrieben. Außerdem kann in Lambda-Universen, was offensichtlich auch in der Natur realisiert ist, ein kosmologischer Term berücksichtigt werden. Die zusätzliche Quelle des Gravitationsfeldes neben der als Flüssigkeit beschriebenen Materie ist dann die Dunkle Energie, die antigravitativ wirkt und die Expansion des Universums beschleunigt. Der metrische Tensor der Robertson-Walker-Metrik ist ebenfalls diagonal, aber mit koordinatenabhängigen Komponenten.

Analysen der Raumzeit mit konformen Metriken: Penrose-Diagramme

In der Analyse von Metriken hat es sich als Vorteil erwiesen, das Verhalten der Raumzeit im Unendlichen mit einer unphysikalischen Metrik zu studieren, die man aus der Raumzeit gewinnt. Man führt eine konforme Transformation durch und gewinnt aus einer gegebenen Metrik eine dazu konforme Metrik. Diese Prozedur ist die Voraussetzung zur Gewinnung von Penrose-Diagrammen, die von großer Relevanz bei der Untersuchung von Raumzeiten in der ART sind.