MOND steht für MOdified Newtonian Dynamics, und es handelt sich dabei um eine alternative Gravitationstheorie. Diese Theorie wurde 1983 von dem israelischen Physiker Mordehai Milgrom publiziert und wird seither von ihm und anderen Wissenschaftlern weiterentwickelt.

Motivation für MOND

Die Newtonsche Gravitation sollte Bewegungen innerhalb von Galaxien gut beschreiben können, weil Gravitationsfelder schwach und Geschwindigkeiten klein sind. Tatsächlich jedoch wurden Abweichungen gefunden, z.B. in der Bewegung von Gaswolken in den rotierenden Scheiben von Spiralgalaxien. Die gemessene Rotation und Zufallsbewegungen sind größer als erwartet. Anders gesagt, es treten Beschleunigungsvariationen auf, die Newtonsch nicht erklärbar sind. Auch die Pioneer-Anomalie besteht in einer rätselhaften Beschleunigung der Sonden Pioneer 10 und 11.
In der konventionellen Astrophysik wird diese Diskrepanz durch die Existenz einer unsichtbaren Materieform, Dunkle Materie (DM), gelöst (Das funktioniert leider nicht beim Pioneer-Problem). Die Dunkle Materie erzeugt dabei eine zusätzliche Gravitationskraft zur sichtbaren, baryonischen Materie und schon sind die rätselhaften Beschleunigungen erklärbar. Im Falle der Galaxien erklärt eine kugelige Verteilung Dunkler Materie um die galaktische Scheibe, das so genannte DM Halo, die gemessenen Rotationskurven recht gut.
MOND stellt nun eine alternative Erklärung für die Beschleunigungen ohne DM bereit. Generell sind Alternativen ohne DM dadurch motiviert, dass bis heute keiner der nicht-baryonischen DM-Kandidaten (z.B. ein exotisches Teilchen) experimentell aufgefunden wurde.

Wie funktioniert MOND?

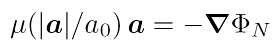Milgroms Ansatz besteht nun in einem modifizierten Newtonschen Gravitationsgesetz in der Form, wie es in der Gleichung rechts dargestellt ist. Die rechte Seite ist gerade der negative Gradient des Gravitationspotentials – genau wie in der Newtonschen Gravitation. Auf der linken Seite steht eine Beschleunigung a, was auch in Übereinstimmung zu Newton ist. Die Modifikation besteht in der neuen Funktion μ, die auf der linken Seite die Newtonsche Beschleunigung modifiziert: Im Fall der Newtonschen Gravitation gilt immer μ = 1 (oder äquivalent a₀ geht gegen 0). Milgrom hat hingegen nun eine glatte, beschleunigungsabhängige Funktion μ angesetzt, die nur bei Beschleunigungen |a| >> a₀ nahe bei 1 liegt. Dabei ist a₀ eine Konstante, die etwa 1.2 × 10^-10 m/s² beträgt. Dieser Zahlenwert resultiert aus MOND-Studien an vielen Galaxien (Begeman et al. 1991). Zwei Vorschläge für den Verlauf von μ zeigt das folgende Diagramm:

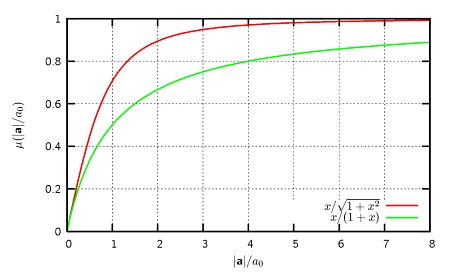
Leistungen von MOND

Dieser Ansatz würde die beobachtete Abflachung der Rotationskurven in Spiralgalaxien erklären, weil bei genügend großem Abstand das neue Milgrom-Gravitationspotential unabhängig vom Radius wird. Ebenso ist MOND konsistent mit der Tully-Fisher-Relation, einer Korrelation zwischen Rotationsgeschwindigkeit und Blauhelligkeit, und den Beobachtungsdaten vieler weiterer Galaxien (Einzelheiten in Bekenstein 2007 und Referenzen darin).
1984 ist es Milgrom und seinem Kollegen Jacob D. Bekenstein (siehe auch Bekenstein-Hawking-Entropie) gelungen, das richtige Lagrange-Funktional (Lagrangian) zu finden, um das angesetzte Kraftgesetz ableiten zu können. Die entsprechend erweiterte Theorie nannten die beiden Autoren AQUAL, ein Akronym, das Aquadratic Lagrangian Theory bedeutet. Aus AQUAL folgt der Ansatz mit der μ-Funktion oben tatsächlich mathematisch. Der AQUAL-Lagrangian gewährleistet auch die Erhaltungssätze für Energie, Impuls und Drehimpuls, die von fundamentaler Bedeutung in der Physik sind. Außerdem ist AQUAL konsistent mit dem schwachen Äquivalenzprinzip.

relativistische Version von MOND

MOND ist eine veränderte Newtonsche Gravitation, aber im Kern ist sie ein Newtonsches Konzept. In der modernen Astrophysik sind jedoch viele Beobachtungen nur mit relativistischen Modellen zu verstehen – der Gravitationskollaps auf ein kompaktes Objekt, die Annäherung von Neutronensternen in einem Doppelsternsystem aufgrund der Emission von Gravitationswellen oder die Expansion des Universums im Rahmen der Kosmologie beispielsweise. Vermag die Milgrom-Theorie auch solche 'Extremfälle der Gravitation' zu beschreiben?
Die ersten Versuche einer relativistischen Verallgemeinerung von MOND mündeten in RAQUAL (relativistische AQUAL) und einer Feldtheorie mit zwei Skalarfeldern namens Phasengekoppelte Gravitation (engl. phase-coupled gravity, PCG). Beide Theorien wurden jedoch aufgegeben: In RAQUAL traten akausale Überlichtgeschwindigkeitseffekte auf. Es wurde versucht, dies in PCG zu beheben, doch diese Feldtheorie entpuppte sich als nicht verträglich mit Beobachtungen im Sonnensystem (Drift der Kepler-Konstante a³/P² aus dem dritten Kepler-Gesetz).
Auch die Implementation eines neuen Vektorfelds in AQUAL durch R.H. Sanders 1997 brachte neue Einsichten, doch alte Probleme: Zwar war diese relativistische Variante von MOND nun mit beobachteten, kosmologischen Gravitationslinsen verträglich, aber man handelte sich mit dem Vektorfeld eine ausgezeichnetes Bezugssystem im Kosmos ein – das ist nicht vereinbar mit dem kosmologischen Prinzip und sollte eine neue Form von 'Äther' bedingen, den die Physiker doch erfolgreich mit der Relativitätstheorie los geworden sind. Sanders relativistische MOND-Version war außerdem nicht kovariant.
Erst wenn das neue Vektorfeld dynamisch wird, können diese Probleme beseitigt werden. Das Resultat wird TeVeS genannt. Dieses Akronym steht für Tensor-Vector-Scalar theory of gravity, also Tensor-Vektor-Skalar-Gravitationstheorie. TeVeS wurde 2004 erstmals von Bekenstein formuliert und wird seither weiterentwickelt. Die Bezeichnung ist plausibel, weil diese Gravitationstheorie durch einen Tensor, einen zeitartiger Vektor und einen Skalar konstruiert wird. Das ist ein klarer Unterschied zu Einsteins Allgemeiner Relativitätstheorie (ART), eine Gravitation, die nur durch einen Tensor, den metrischen Tensor, vermittelt wird. Die Unterschiede treten auf dem feldtheoretischen Niveau zutage, wenn man die Lagrangians der beiden Theorien vergleicht: Die ART basiert auf der Einstein-Hilbert-Wirkung, die nur von der Determinante des metrischen Tensors abhängt; TeVeS involviert dagegen weitere Terme im Lagrangian, die von dem neuen Vektor und dem neuen Skalar abhängen. Dennoch verhält sich die Kosmologie mit TeVeS in vielerlei Hinsicht so wie die Einsteinsche Kosmologie.

GR mit DM vs. TeVeS ohne DM

Kosmologische Gravitationslinsen sind im konventionellen Bild hohe und dichte Ansammlungen von normaler und Dunkler Materie. Die Standard-Gravitationsphysik besagt, dass sowohl normale Materie, als auch Dunkle Materie jeweils für sich genommen ein Gravitationspotential erzeugen, die beide an dem Licht 'ziehen'. In TeVeS gibt es keine Dunkle Materie. Daher bleibt nur das Gravitationspotential der normalen Materie bestehen, und den Part der Dunklen Materie übernimmt in TeVeS eine nicht-lineare Gleichung der AQUAL-Theorie.

aktueller Stand und kritische Einschätzung

MOND und dessen relativistische Erweiterung TeVeS sind Theorien in der Gravitationsforschung, die sich deutlich vom Mainstream absetzen. Ganz objektiv betrachtet gibt es unter Gravitationsforschern und Physikern zurzeit deutlich mehr Anhänger am Standardmodell mit Dunkler Materie, als an MOND/TeVeS. Diese Beobachtung bedeutet jedoch gar nichts, weil in den Naturwissenschaften die bewährten Theorien gewinnen. Es wird sich also in einem langwierigen Prozess erweisen, welche Theorie die Natur am besten beschreibt.
Mit Blick auf die Struktur von TeVeS könnte man kritisch das Prinzip minimaler gravitativer Kopplung anführen, das im Kern ein Plädoyer für eine genügend einfache Theorie ist. Ist nun eine Gravitationstheorie einfach, die Tensor, Vektor und Skalar erfordert? Oder ist eine Theorie einfach, die nur tensoriell ist, aber eine zusätzliche Materieform postuliert, die nie direkt beobachtet wurde? Darüber kann man sicher streiten.
Der moderne, orthodoxe Kosmologe mag MOND/TeVeS-Theorien mit dem Einwand abschmettern wollen, dass das ΛCDM-Konsensmodell bestens mit den Beobachtungen an der kosmischen Hintergrundstrahlung (CMB) und Supernovae Ia vereinbar sei. Doch kürzlich ist es gelungen, dass das CMB-Spektrum mit einer TeVeS-Kosmologie ohne Dunkle Materie erklärt werden könne (Skordis et al. 2006): Die kosmologische Konstante bliebe dann erhalten, und eine massereiche Form von Neutrinos (mit einer Masse noch innerhalb tolerabler Grenzen des Standardmodells) wäre vonnöten. Aktuell deutet sich in einigen TeVeS-Modellen sogar an, dass auch auf die rätselhafte Dunkle Energie verzichtet werden könne, falls eine TeVeS-Gravitation bemüht werde. Diese Entwicklungen sind sicherlich äußerst interessant – aber erst viele überstandene Hypothesentests von MOND/TeVeS werden das Gros der Wissenschaftler überzeugen, die fest an die Existenz von Dunkler Materie und Dunkler Energie glauben.

Originalveröffentlichungen & Quellen

• Milgrom, M.: A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis, ApJ 270, 365, 1983
• Bekenstein, J. D.: The modified Newtonian dynamics – MOND – and its implications for new physics, Preprint unter astro-ph/0701848, 2007