Neutronensterne sind stabile Endkonfigurationen, die aus dem Gravitationskollaps massereicher Sterne entstehen. Massereiche Sterne durchlaufen alle Brennstoffzyklen thermonuklearer Fusion bis sie im Innern einen Eisenkern (vergleiche Nife-Kern der Erde) gebildet haben. Dieser Vorläufer des Neutronensterns (engl. neutron star progenitor) weist typische Massen von 1.2 bis 1.6 Sonnenmassen auf.

Zusammenfall & Explosion

Da weitere exotherme Reaktionen im Innern nach der Phase des Siliziumbrennens unterbleiben, ist das hydrostatische Gleichgewicht des Sterns gestört: der Strahlungsdruck (ebenso der Gasdruck, der über Strahlungstransport an den Strahlungsdruck koppelt) verringert sich im Sterninnern rapide, was zugunsten des Gravitationsdrucks geht. Die Konsequenz ist katastrophal: Der innere Teil des sterbenden Sterns fällt im Gravitationskollaps in sich zusammen. Durch die einlaufende Schockwelle wird die Sternmaterie stark komprimiert. Irgendwann ist die Materie so dicht, dass die Schockwelle daran reflektiert wird (rebounce). Als Folge dessen läuft eine etwa kugelförmige Schockfront wieder nach außen, reißt die äußeren Sternschichten mit sich und produziert eine spektakuläre Supernova-Explosion (Typ II). In diesem letzten Aufflammen wird der sterbende Stern gleißend hell und überstrahlt sogar das Licht seiner Heimatgalaxie. Erstaunlicherweise geht die meiste freigesetzte Energie dieser Explosion gar nicht in elektromagnetische Strahlung, sondern in die Neutrinos.

kosmische Häufigkeit

Allein in der Milchstraße gibt es mehr als 100 Millionen Neutronensterne – bei insgesamt einigen hundert Milliarden Sternen also anteilig im Promillebereich.

Pulsare: kosmische Leuchttürme

Zahlreiche Neutronensterne können die Astronomen beobachten und als Pulsare identifizieren. Von ihnen nahm man zunächst an, dass es sich um pulsierende Sterne handelt (daher der Name). Die scheinbar gepulste Strahlung kommt jedoch durch Rotation eines Neutronensterns zustande. Dabei sitzt die Strahlungsquelle an einem der magnetischen Pole des Neutronensterns. Differieren nun Rotations- und Magnetfeldachse, so dreht sich der Strahlungskegel um den Neutronenstern im Raum wie bei einem Leuchtturm. Diese geometrische Restriktion macht klar, dass Astronomen bei weitem nicht alle Neutronensterne in Form von Pulsaren beobachten können. Denn in der Regel wird der enge Strahlungskegel an der Erde vorbei schwenken.

Neutronensternjagd mit Röntgenteleskopen

In kompakten Röntgendoppelsternen (engl. Akronym XRBs für X-ray binaries) kann man aus den Kepler-Gesetzen indirekt auf die Existenz von Neutronensternen schließen, auch wenn man keine Pulsarstrahlung misst. Hier verraten sich die Neutronensterne durch die gemessene Sternmasse, die in einem bestimmten Massenbereich liegt (dazu im nächsten Absatz mehr). Eine weitere Methode des indirekten Nachweises sind charakteristische Strahlungssignaturen wie Strahlungsausbrüche. Diese können Folge eines Sternbebens (engl. star quake) in der Neutronensternkruste sein oder durch Akkretion der Materie eines Begleiters auf die Neutronensternoberfläche hervorgerufen werden.

Was wiegen die schwersten Neutronensterne?

Eine strittige Frage aus theoretischer Sicht ist, wie schwer Neutronensterne werden können. Die Astrophysiker wissen, dass sie schwerer werden können als Weiße Zwerge, aber ab einer bestimmten Massengrenze nicht mehr stabil sind. Denn dann kollabiert ein Neutronenstern zu einem stellaren Schwarzen Loch.
Die klassische Massengrenze von Neutronenmaterie ist die Oppenheimer-Volkoff-Grenze von 0.7 Sonnenmassen, die bereits 1939 berechnet wurde. Dieses Neutronensternmodell ist jedoch nicht wirklichkeitsnah, weil Neutronensterne viel komplexer aufgebaut sind, wie die Kernphysiker mittlerweile wissen. Ein anderer konservativer Zahlenwert für die Maximalmasse eines Neutronensterns resultiert aus sehr allgemeinen Überlegungen auf der Basis von Einsteins Allgemeiner Relativitätstheorie und beträgt 3.2 Sonnenmassen (Rhoades & Ruffini, PRL 1974). Neuere Arbeiten setzen dieses Limit deutlich herab: So wird ein Massenbereich für Neutronensterne wird zwischen 1.5 und 1.8 Sonnenmassen diskutiert (Burgio 2004, nucl-th/0410040). Andere Autoren finden kleinere Maximalmassen, z.B. kleiner als 1.4 Sonnenmassen, wenn nur baryonische Materie im Neutronensterninnern angenommen wird; sobald jedoch eine Komponente nicht-baryonischer Materie, nämlich Quarkmaterie dazukommt, kann ebenfalls eine Maximalmasse von etwa 1.8 Sonnenmassen abgeleitet werden (Schulze et al., Phys. Rev. C 2006). Die neueren Zahlenwerte folgen im Rahmen der theoretischen Kernphysik.
Nach wie vor, ist dieser Massenbereich unsicher und Gegenstand der Forschung, weil das Innere der Neutronensterne nicht vollständig geklärt ist. In üblichen Modellen besteht das Innere des Neutronensterns in den äußeren Zonen aus Neutronen und Hyperonen (als hadronische Phase), und der Sternkern besteht aus Quarks (Quarkphase). Die größte Unsicherheit steckt in der Zustandsgleichung und in der Frage, wie Hadronen in Quarks bei hohen Dichten übergehen. Wertvolle Hinweise für das richtige Massenregime kommen aus der astronomischen Beobachtung. Entdecken Astronomen z.B. einen Neutronenstern mit mehr als 1.8 Sonnenmassen, so müssen die letztgenannten Modelle korrigiert werden. Leider ist auch die astronomische Messung schwierig und fehleranfällig.

Zweige theoretischer Kernphysik

Ein Neutronenstern besteht aus verschiedenen Materieformen, die in seinem Innern in etwa kugelförmigen Schalen angeordnet sind. Die physikalische Beschreibung dieser Materie unter extrem hohen Dichten ist besonders anspruchsvoll und erfordert Konzepte der Kernphysik und der Quantenfeldtheorien. Ein wesentlicher Zweig aus der Theorie ist dabei die Brückner-Vielteilchentheorie (nicht-relativistisch: Brückner-Hartree-Fock Theorie; relativistisch: Dirac-Brückner-Theorie). Welche Theorie am besten geeignet ist, ist ebenfalls Gegenstand aktueller Forschung.

Neutronisierung

Die Ursache für das Überwiegen der Neutronen ist die ungleich höhere Dichte der Prä-Neutronensterne. Überschreitet die Zentraldichte des Eisenkerns im Gravitationskollaps den kritischen Wert von etwa 1.14 × 10⁹ g cm^-3, setzt der inverse β^--Zerfall ein, der die Materie nach und nach neutronisiert. Dabei fangen die Atomkerne Elektronen ein, und es bilden sich Neutronen, gemäß den ersten beiden Gleichungen rechts (Element X habe die Ordnungszahl Z und eine Atommasse A). Bezogen auf das schwerste Element, das sich im Sternkern gebildet hat, Eisen-56 (⁵⁶Fe), ergibt sich die Reaktionskette links, dritte Abbildung. Es wandelt sich in Mangan (Mn) um, dieses wiederum wird zu Chrom (Cr). Chrom bleibt stabil, bis im Zuge des anhaltenden Kollapses noch höhere Zentraldichten erreicht werden. Ab einer Dichte von 1.5 × 10¹⁰ g cm^-3 zerfällt auch Chrom. Bei noch höheren Dichten, ab 3.9 × 10¹⁰ g cm^-3 kann sich sogar Kohlenstoff zu Elementen kleinerer Ordnungszahl umwandeln (siehe vierte Reaktionsgleichung, rechts). Die Neutronisierung ist demnach ein sukzessiver Vorgang, der die Atomkerne nach und nach mit immer mehr Neutronen anreichert: Sie werden zu neutronenreichen Atomkernen (engl. neutron-rich atomic nuclei). Wie die Reaktionen zeigen, werden aufgrund der Leptonenzahlerhaltung immer Elektron-Neutrinos ν_e frei. Diese wechselwirken nur schwach mit der Umgebung und können (unterhalb der Neutrino-Trapping-Dichte, s.u.) das Sterninnere verlassen, Energie und Wärme wegtragen und damit den Kollaps kühlen. 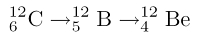Unter normalen, irdischen Bedingungen würden die neutronenreichen Atomkerne schnell zerfallen und zum Betastrahler werden. Dies geschieht im Neutronenstern jedoch nicht, weil sich die Neutronen bei diesen hohen Plasmadichten im Gleichgewicht mit Protonen und Elektronen befinden. Physikalisch formuliert liegt das daran, weil die Fermienergie des entarteten Elektronengases in der Größenordnung der Zerfallsenergie der Neutronen ist (etwa 780 keV).

Nehmen wir ein Neutrinobad

Es gibt weitere Prozesse, bei denen Neutrinos unterschiedlichen Typs emittiert werden können. So kommt es zur Paarvernichtung (Paarannihilation) von Elektron und Positron (Austausch von W- und Z-Teilchen der schwachen Wechselwirkung). Dies zeigt die fünfte Reaktionsgleichung links. Es handelt sich hierbei um den so genannten Plasmon-Zerfall, wobei l ein Platzhalter für alle drei Typen der Leptonenfamilie ist: Elektron, Myon und Tauon. D.h. alle möglichen Neutrinos können dabei entstehen! Im Gegensatz zur Sonne, die nur Elektronneutrinos aussendet (die jedoch danach in andere Typen oszillieren), emittieren sterbende, massereiche Sterne von Anfang an Neutrinos aller drei Familien.
Außerdem entstehen Neutrinos in der Photo-Annihilation (siehe siebte Gleichung, rechts).
Auch bei der Emission von Bremsstrahlung werden weitere Neutrinos freigesetzt (achte Gleichung, links). Insgesamt bildet sich ein Neutrinobad aus.

Neutronisierungsgegner

Es gibt zur Neutronisierung auch konkurrierende Prozesse, so genannte pyknonukleare Reaktionen (grch. pyknos: dicht), die bei sehr hohen Dichten ablaufen können. Cameron (1959) sowie Van Horn und Salpeter (1969) konnten zeigen, dass sich auf einer typischen Zeitskala von etwa 100 000 Jahren

• Wasserstoff in Helium (oberhalb etwa 10⁶ g/cm³),
• Helium-4 in Kohlenstoff-12 (oberhalb etwa 8 × 10⁸ g/cm³),
• und Kohlenstoff-12 in Magnesium-24 (oberhalb etwa 10¹⁰ g/cm³)

umwandeln können. Je nach Verhältnis von Hin- und Rückreaktionen findet so allmählich eine Neutronisierung statt. Da die Zeitskala des Gravitationskollapses weit kürzer ist, als diejenige der pyknonuklearen Reaktionen, gewinnt schließlich die Neutronisierung: ein Neutronenstern ist entstanden!

Quantendruck stabilisiert

Innerhalb der Sternrestmassen von etwa 1.2 bis 3.2 Sonnenmassen (nehmen wir mal die konservative Maximalmasse an) bildet sich eine stabile Konfiguration aus, die vor allem durch den Entartungsdruck der Neutronen stabilisiert und so vom Kollaps im freien Fall aufgehalten wird. Dieser Quantendruck hat dieselbe Natur wie bei Weißen Zwergen, nur dass das Fermionengas großteils aus Neutronen besteht und nicht aus Elektronen – sie sind nur eine Beimischung im Innern von Neutronensternen. Fermionen unterliegen dem Pauli-Prinzip und können nicht in allen Quantenzahlen übereinstimmen. Sie können nur dann denselben Zustand besetzen, wenn ein Neutron Spin 'nach oben' (engl. spin-up) und das andere im gleichen Zustand Spin 'nach unten' (engl. spin-down) hat. Anschaulich gesprochen, können sich die Neutronen nicht (wie die Bosonen) beliebig nahe kommen, was einem Druck, dem Entartungsdruck, entspricht. Das ist die tiefe, physikalische Ursache für die Existenz von Neutronensternen. Die Berechnung des Entartungsdruckes erfolgt im Rahmen der statistischen Physik: Die Theoretiker setzen eine Phasenraumbeschreibung an. Hier integrieren sie über alle möglichen Impulszustände der Neutronen, von Impuls null bis zum Fermi-Impuls ('Integration über die Fermi-Kugel'). Daraus resultiert der Entartungsdruck, der dann die Gestalt einer polytropischen Zustandsgleichung hat und nur in einer Potenz von der Massendichte abhängt. Anschaulich bedeutet dies: je dichter das Material (die Neutronen) gepackt ist, umso entscheidender wird der Einfluss des Pauli-Prinzips, das dann bei hoher Kompression eine neue Druckkomponente bereitstellt.
In einer Abschätzung des Verhältnisses der Massen von Neutronen zu Elektronen, was einen Faktor von etwa 1840 liefert, wird unmittelbar klar, weshalb die Neutronensterne notwendigerweise sehr viel kleiner sein müssen, als Weiße Zwerge.

Die 4-Parameter-Raumzeit von Neutronensternen

Die Raumzeit oder Metrik außerhalb der Oberfläche eines Neutronensterns ist ebenso wie die eines rotierenden Schwarzen Loches (der so genannten Kerr-Lösung) stationär und axialsymmetrisch. Vor wenigen Jahren wurde eine exakte Formulierung dieser Metrik in gebrochenrationalen Polynomen gefunden (Manko et al., 2000, gr-qc/0001081), die mathematisch etwas komplizierter ist als für Kerr-Löcher. Der entscheidende Unterschied ist, dass Neutronensterne – im Gegensatz zu Schwarzen Löchern, die 'keine Haare' haben (Keine-Haare-Theorem) – mehr Eigenschaften aufweisen. Neutronensterne werden durch ihre Masse, ihren Drehimpuls sowie durch ihr Massen-Quadrupolmoment und ihr magnetisches Moment charakterisiert. Daraus resultiert eine 4-Parameter-Klasse von Lösungen für die Einstein-Maxwell-Gleichungen (siehe dazu Maxwell-Tensor) der Allgemeinen Relativitätstheorie.

Ganz schön dicht!

Neutronensterne gehören zu den kompakten Objekten: sie haben nur Radien von etwa 15 km, aber Massen von etwa 1.5 Sonnenmassen! Beide Wertebereiche werden durch astronomische Beobachtungen gestützt. Die Kernmateriedichte liegt – wie aus der Kernphysik bekannt – bei 0.17 fm^-3, 140 MeV fm^-3 oder 2.5 × 10¹⁴ g cm^-3 im cgs-System. Aus diesen bekannten, typischen Werten für Masse und Radius kann eine mittlere Dichte der Neutronensterne von etwa 2 × 10¹⁵ g cm^-3 abgeleitet werden. Das entspricht demgemäß mehrfacher Kernmateriedichte (supranukleare Dichten), genau genommen knapp zehnfache.
Das Innere eines Neutronensterns muss daher mit einer Physik der hohen Dichten beschrieben werden. Es stellt sich heraus, dass eine konsistente Beschreibung des Innern mit einer einzigen Theorie nicht möglich ist, sondern man in verschiedenen Dichteregimes unterschiedliche Theorien verwenden muss. Dies ist im Wesentlichen der Grund dafür, dass man keinen festen Grenzwert für die Maximalmasse eines Neutronensterns angeben kann. Es ist allenfalls möglich ein unteres und ein oberes Limit aus einer Synopsis der Theorien anzugeben.

Wir schneiden einen Neutronenstern auf

Im Folgenden sind die Dichtebereiche und assoziierte, physikalische Modelle kurz skizziert. Neutronensterne sind – wie obige Kalkulation der mittleren Dichte nahe legt – wesentlich dichter als die Weißen Zwerge. Zunächst kann man das Innere der Neutronensterne in Kruste und Kern unterteilen. Die Kruste besteht, wie mit der Sternentwicklung nachzuvollziehen ist, aus einem Coulomb-Gitter von Eisen-56-Atomkernen und einem Fermigas entarteter Elektronen. Die Festkörperphysik liefert den theoretischen Rahmen einer Beschreibung. Der Kern setzt sich aus einer Neutronenflüssigkeit, einigen Elementarteilchen und einer Quark-Phase zusammen. Hier muss man auf Methoden der Kernphysik, Quantenchromodynamik (QCD) und Teilchenphysik zurückgreifen.
Es erweist sich als sinnvoll Kruste und Kern weiter zu unterteilen, weil die Zustandsgleichungen und die zugehörigen Teilchenspezies und Teilchenphasen in den unterschiedlichen Dichteschalen stark differieren. Unterhalb der dünnen, nur etwa einen Kilometer durchmessenden Neutronensternkruste vermutet man drei wesentliche Phasen von Materie, die miteinander im Gleichgewicht stehen:

• eine normale hadronische Phase, bestehend aus neutronenreichen Atomkernen und einer Neutronenflüssigkeit,
• eine Phase aus kondensierten Kaonen (eine bestimmte Form von Mesonen, bestehend aus einem Quark und einem Antiquark)
• und eine Quark-Phase (QP) oder auch Quark-Gluonen-Plasma (QGP) genannt.

In der theoretischen Kernphysik gilt die Hadronenphase als gut etabliert. Für dessen Beschreibung verwendet man die relativistische Mean-field-Theorie (RMF). Im Speziellen handelt es sich um den Brueckner-Bethe-Goldstone-Formalismus, wo man die Nukleon-Nukleon-Wechselwirkung mit dem Paris-Potential und Drei-Körper-Kräfte mit dem Urbana-Modell beschreibt. Als Additiv berücksichtigt man die Hyperon-Nukleon-Wechselwirkung.
Die Quark-Kondensation und die Existenz von Kaonen sind eine Folge der spontanen Brechung der chiralen Symmetrie (einer bestimmten Symmetrie des QCD-Lagrangian). Dann treten nämlich fast masselose, so genannte Goldstone-Bosonen auf, wie Pionen, das η-Teilchen oder eben Kaonen. So gibt es im Innern der Neutronensterne Prozesse, wo ein Bose-Kondensat aus Kaonen entsteht (siehe die nächsten beiden Reaktionsgleichungen).

Rolle der Kaonen

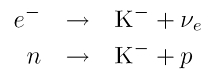Neben den Nukleon-Nukleon-Wechselwirkungen werden dann auch Kaon-Nukleon-Wechselwirkungen relevant. Dies beeinflusst maßgeblich Transport- und Kühlungsprozesse im Innern. In der Zustandsgleichung gibt es somit für die Energiedichte der Neutronensternmaterie einen Beitrag von den Kaonen; für den Gesamtdruck gibt es keinen Beitrag von Kaonen, weil sie Bosonen sind und somit kein Partialdruck entsteht. Kaonen 'weichen die EoS auf', so dass eine Maximalmasse für Neutronensterne durch ihren Einfluss reduziert wird. Außerdem erwartet man einen Einfluss der Kaonen auf die Entwicklung des Prä-Neutronensterns während des Supernova-Kollapses.

Quarkmaterie

Bei mehrfacher Kernmateriedichte erwartet man einen Übergang zu Quarkmaterie, die einerseits aus Quarkpaaren und andererseits aus dem Quark-Gluonen-Plasma besteht. Die Beschreibung der ersten Komponente, den so genannten Diquarks, ist analog zur BCS-Theorie der Supraleitung in Festkörpern, nur dass die Cooper-Paare nicht aus Elektronen, sondern aus Quarks bestehen. Daher rührt die Bezeichnung Farbsupraleitung. Vermutlich spielt sie neben Neutronensternen auch im Innern so genannter Quarksternen eine Rolle.

Die Beschreibung der Quarkphase gestaltet sich weit schwieriger. Hier nutzt man ein eher phänomenologisches Modell (darin liegt eine Schwäche) und beschreibt sie mit dem MIT Bag-Modell (Näheres dazu bei den Quarksternen). Die obige Abbildung zeigt schematisch in einem QCD-Phasendiagramm, wie die drei Phasen voneinander abgrenzen.

Aus diesen Überlegungen ergibt sich insgesamt folgende Schalenstruktur eines Neutronensterns (Abbildung oben):

• Um den Neutronenstern herum befindet sich eine nur wenige Zentimeter durchmessende Atmosphäre.
• Der eigentliche Neutronenstern hat am Rand eine äußere Kruste, die aus einem Gitter von Atomkernen, vor allem Fe-56, und einem Fermigas relativistisch entarteter Elektronen besteht. Nach innen setzt die Neutronisierung ein, die zunächst nur die Atomkerne mit Neutronen anreichert.
• Dann schließt sich eine innere Kruste an, die aus einer warmen Neutronenflüssigkeit und einem Gitter neutronenreicher Atomkerne besteht. Diese Zone wird außen durch diejenige Dichte definiert, bei der die Neutronen aus den mit Neutronen stark übersättigten Atomkernen 'austropfen'. Bei einer Dichte von etwa 4 × 10¹¹ g cm^-3, der so genannten neutron drip density, ist die Bindungsenergie der Neutronen an den Atomkern so gering, dass sie in 'Tropfen' den Kernverbund verlassen können. Daher nennt man diese Phase auch Neutronenflüssigkeit. Inwärts schließt die innere Kruste bei der Übergangsdichte von 1.7 × 10¹⁴ g cm^-3 ab: bei diesen Dichten ist die Neutronisierung abgeschlossen und kein Atomkern mehr vorhanden.
• Nun schließt sich der äußere Kern an, wo alle Atomkerne in ihre Bestandteile zerlegt wurden: den Nukleonen, also den Protonen und den Neutronen. Daneben existieren immer noch Elektronen als entartetes Fermigas. Der äußere Kern enthält neben diesen Spezies auch besonders massive Baryonen, die Hyperonen und auch die Kaonen. Die Hyperonisierung setzt bei typischen Dichten im Bereich von zwei- bis dreifacher Kernmateriedichte ein. In Überlappungsbereich zwischen äußerem und innerem Kern sollten bereits Beimischungen der farbsupraleitenden Phase, also Diquarks, existieren.
• Tief im Innersten, dem inneren Kern, wurden auch die Nukleonen aufgebrochen. Hier erwartet man, dass der Einschluss (confinement) der Quarks aufgehoben wird und sie in freier Form im Gleichgewicht mit ihren ebenfalls Farbe tragenden Austauschteilchen, den Gluonen, existieren: dies ist die Domäne des QGPs. Quarks und Gluonen bewegen sich quasi-frei und bilden eine plasmaartige Phase. Dieser besonders exotische Materiezustand wird unter ultrahohen Dichten (fünf- bis zehnfache Kernmateriedichte) und enormen Temperaturen von einer Billion Grad (entsprechend 150 MeV) erreicht. Das QGP ist noch Physik innerhalb des Standardmodells der Teilchenphysik und im Rahmen der QCD ableitbar.

So nimmt die Dichte nach innen zu

Die letzte Abbildung dieses Lexikoneintrages zeigt den Verlauf des Dichtegradienten im Innern eines Neutronensterns. Man erkennt, dass die supranuklearen Dichten vor allem im inneren Kern angenommen werden und das Quark-Gluonen-Plasma bilden. Natürlich sind die numerischen Werte für die Dichten, ebenso wie die Radien der Schalen modellabhängig, und es gibt noch keine Formulierung, die bis auf die Nachkommastelle einheitlich ist. Ebenso ist die Einteilung in Schalen relativ willkürlich, weil man auch noch mehr Substrukturen einbauen könnte (Hyperonenschale o.ä.).

Ein Neutronensternschicksal

Nach Kenntnis dieser Ingredienzien für die Zustandsgleichungen eines Neutronensterns bestimmt man über die klassische Tolman-Oppenheimer-Volkoff-Gleichung die Obergrenze für die Masse eines Neutronensterns. Oberhalb dieser Grenzmasse muss auch der Neutronenstern kollabieren und wird aller Wahrscheinlichkeit nach ein stellares Schwarzes Loch. Dieses Szenario ist denkbar, wenn beispielsweise in einem Doppelsternsystem eine der beiden Komponenten im Rahmen der Sternentwicklung zu einem Neutronenstern wurde. Ist die andere Komponente ein Riesenstern, der sein Roche-Volumen überschreitet, kann Materie des Riesen durch den inneren Lagrange-Punkt des Systems auf die kompakte Komponente überfließen. Durch Akkretion kann somit ein Neutronenstern an das Limit seiner Stabilitätsgrenze getrieben werden und bei Überschreitung des Limits weiter kollabieren.
Die Unfähigkeit, eine klare Grenzmasse analog zur Chandrasekhar-Grenze Weißer Zwerge angeben zu können, resultiert aus einer Unsicherheit in den Zustandsgleichungen. Die Theorie des Neutronensterninnern ist noch nicht eindeutig und die Kern- und Elementarteilchenphysik lässt noch Spielraum für die Massengrenze. Die Forschung engt diesen jedoch sukzessive ein und führt sogar auf mögliche Unterklassifikationen von Neutronensternen.

Masse-Radius-Relationen

Hinzu kommt, dass selbst bei eindeutiger theoretischer Kenntnis der Zustandsgleichung, diese nur äußerst schwierig in der Beobachtung verifiziert werden kann. Die Astronomen können natürlich nicht ins Innere der Neutronensterne hineinblicken und müssen indirekt – beispielsweise über die äußere Gestalt des Sterns (Radiusmessungen) oder hochenergetischen Strahlungsausbrüchen – auf das Innere und die Richtigkeit von Zustandsgleichungen schließen. Über Messungen der Masse-Radius-Relationen aus Pulsardaten versuchen Astronomen diese Kenntnis zu erlangen. Die typische Masse-Radius-Relation eines Neutronensterns lautet M ~ R^-3, was in starkem Gegensatz zu den kompakteren Strange Stars steht, M ~ R⁺³! Astronomische Messungen von Masse (Kepler-Gesetze) und Radius (Fluss messen bei bekannter Distanz) an verschiedenen Kompakten Objekten, sollten Vertreter der jeweiligen Klasse enthüllen oder wenigstens einen schwachen Hinweis zur Unterscheidung geben.

Irdische Neutronensternmaterie

Die Frage, ob im tiefsten Innern von Neutronensternen tatsächlich neue Physik vorgefunden werden kann, ist Gegenstand aktueller Forschung. Die extremen Materiebedingungen versuchen die Physiker im Labor nachzustellen. Die Forschung wird u.a. mit dem TeilchenbeschleunigerRHIC (Relativistic Heavy Ion Collider) und an der GSI (Gesellschaft für Schwerionenforschung) Darmstadt und bald auch am LHC (Large Hadron Collider) am CERN betrieben. Extreme Materiezustände wie das extrem kurzlebige QGP können aus den Stößen sehr schwerer Ionen wie Gold- oder Bleiatomkerne erzeugt werden. Denn bei solchen Zusammenstößen werden kurzfristig auf sehr kleinen Raumskalen Dichten wie im Innern von Neutronensternen erreicht. Tatsächlich gelang den RHIC-Physikern die Erzeugung eines QGPs im Jahr 2004, wie unter dem Eintrag Quark-Gluonen-Plasma beschrieben wird.
Teilchenphysiker untersuchen auch die Produktion von Kaonen. Die messtechnischen Anforderungen solcher Experimente sind außerordentlich hoch! Die Physiker hoffen, dass irdische Teilchenbeschleuniger den Bereich hoher Dichte und hoher Temperatur ausloten, während astronomische Beobachtungen von Neutronensternen den Bereich hoher Dichten und niedriger Temperaturen liefern. In dieser Forschung zeigt sich abermals eine Annäherung von Teilchenphysik und Astrophysik, wie in der Kosmologie.

Magnetare: stark magnetisierte Neutronensterne

Stark magnetisierte Neutronensterne nennt man Magnetare, die Pulsare haben sich als rotierende Neutronensterne erwiesen.

Neutronensterne im Doppelpack

Ein Binärsystem aus Neutronensternen, der Hulse-Taylor-Pulsar mit der Katalogbezeichnung PSR 1913+16, erlangte Berühmtheit, weil es bei diesem System gelang, indirekt die Abstrahlung von Gravitationswellen nachzuweisen. Dies war ein weiterer, gewichtiger Beleg für die Existenz von Gravitationswellen und die Richtigkeit der Allgemeinen RelativitätstheorieAlbert Einsteins.