Der Plancksche Strahler ist vermutlich das wichtigste Strahlungsgesetz in der Astronomie. Das liegt daran, weil sehr viele Quellenelektromagnetischer Strahlung im Universum durch ein solches Strahlungsgesetz beschrieben werden. Es handelt sich dabei um Wärmestrahlung, d.h. die elektromagnetische Emission wird von elektrischen Ladungen (in der Regel Elektronen, Protonen, Ionen) abgegeben, die sich aufgrund von Wärme bewegen.

Terminologie

Plancksche Strahler werden auch als Hohlraumstrahler, Schwarze Strahler oder Schwarze Körper (engl. black body, BB) bezeichnet. Der etwas allgemeine Name Wärmestrahler oder thermischer Strahler ist ebenfalls verbreitet.

Beispiele

Beispiele für Planck-Strahler aus dem Alltag sind eine Kerzenflamme, unsere Haut, ein Eiswürfel, eine Tasse Kaffee – eigentlich strahlt alles Wärmestrahlung ab, weil jeder Gegenstand eine endliche Temperatur hat. Einen Zustand endlicher Temperatur verlangt gerade der dritte Hauptsatz der Thermodynamik. Bei welcher Strahlungsenergie (Farbe) die höchste Strahlungsintensität liegt, bestimmt gerade die Temperatur des Strahlers.
Die kosmischen Planck-Strahler sind beispielsweise die kosmische Hintergrundstrahlung, fein verteilter, interplanetar Staub im Sonnensystem (siehe auch Zodiakallicht), das relativ kühle interstellare Medium in der Milchstraße, heißes intergalaktisches Gas, das zwischen den Galaxien in Galaxienhaufen zu finden ist, natürlich auch die Oberflächen von Sternen (siehe Effektivtemperatur und Spektraltyp) oder auch die Standardscheiben, die um diverse kosmische Objekte (Protosterne, Weiße Zwerge, Schwarze Löcher) rotieren.

Geschichtliches

Der Plancksche Strahler wurde nach dem deutschen Physiker Max Planck (1858 – 1947) benannt. Er ist ein Pionier der Quantentheorie, weil er die Quanten der Wärmestrahlung im Jahr 1900 entdeckt hat (Nobelpreis für Physik 1918). Erst später wurde klar, dass Licht und elektromagnetische Strahlung generell quantisiert sind (Einsteins Lichtquantenhypothese 1905, siehe auch Photon).

Das Planck-Spektrum

Ein Planck-Strahler gibt Wärmestrahlung als kontinuierliches Spektrum über einen theoretisch beliebig großen Spektralbereich ab. Die Plancksche Strahlungsverteilung ist jedoch nicht konstant über alle Wellenlängen oder extrem schmal wie eine Spektrallinie: es ist eine recht breite Verteilung, die ein Maximum bei einer bestimmten Wellenlänge der Strahlung (Strahlungsfrequenz, -energie) annimmt. Die Position dieses Maximums und das Profil der Verteilung diktiert einzig die Temperatur als wichtigster Parameter eines Planck-Strahlers.
Die Gestalt einer Planckschen Strahlungsverteilung in Abhängigkeit von der Temperatur zeigt die folgende Abbildung:

Dabei entsprechen 0 Kelvin gleich -273.16° Celsius, so sind z.B. 1000 Kelvin gleich 726.84° Celsius. In der Horizontalen ist die Wellenlänge der Strahlung in Mikrometern (10^-6 Metern) angegeben. Die Größe in der Vertikalen heißt spektrale Strahlungsdichte und ist ein Maß für die Strahlungsintensität des Planckschen Strahlers. Wie man in den Beispielen gut erkennen kann, verschiebt sich das Maximum der Verteilung zu kleineren Wellenlängen, wenn die Temperatur des Strahlers anwächst. Deshalb kann ein besonders heißer Körper auch optische Planck-Strahlung abgeben. Der linke Rand im Diagramm entspricht gerade 0.5 μm = 500 nm, also grünem Licht. Der rechte Rand ist der Bereich der Infrarotstrahlung.

Wo liegt das Strahlungsmaximum?

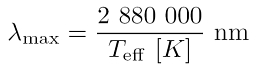Das Maximum der Planckschen Strahlungsverteilung kann mit dem Wienschen Verschiebungsgesetz berechnet werden (siehe Gleichung rechts, nachzurechnen mittels Kurvendiskussion der Strahlungsformel unten). Dieser Zusammenhang wurde 1893 von dem deutschen Physiker Wilhelm Karl Werner Wien (1864 – 1928) gefunden. Einsetzen der Temperatur liefert die Wellenlänge am Strahlungsmaximum. Dieses Maximum bestimmt, bei welcher Strahlungsenergie (=Farbe) der Plancksche Strahler die höchste Strahlungsintensität erreicht. Einfacher gesagt: Die Temperatur bestimmt, wie uns ein Körper erscheint und welche Strahlungsdetektoren man verwenden sollte, um die thermische Strahlung zu messen.
Unsere Haut leuchtet deshalb bei etwa 10 μm im Nahinfrarot. Die einige hundert Grad heiße Glut im Feuer erscheint uns daher rot. Die Sonne mit etwa 6000 Grad Oberflächentemperatur sehen wir als gelben Stern. Ein an der Oberfläche extrem heißer Weißer Zwerg erscheint blau-weiß.

Die Strahlungsformel

Für diejenigen, die es ganz genau wissen wollen, wird im Folgenden die Plancksche Strahlungsformel vorgestellt, um die Planck-Spektren berechnen zu können. Dabei wird vereinfachend Isotropie der Strahlung vorausgesetzt, was mit einem Faktor 4π in den Strahlungsformeln beiträgt. Was bei der Berechnung Schwierigkeiten bereiten kann, ist die korrekte Umrechnung, je nachdem ob man die Planck-Verteilung als Funktion der Wellenlänge, der Strahlungsfrequenz oder der Strahlungsenergie ausdrückt.
Generell berechnet sich die totale Energiedichte der Strahlungu = U/V aus einem Integral über die spektrale Energiedichte u_ν. Je nachdem, ob man über Wellenlänge λ, Frequenz ν bzw. ω = 2πν oder Energie E integriert, entscheidet man sich für eines der folgenden vier Integrale (große Version):

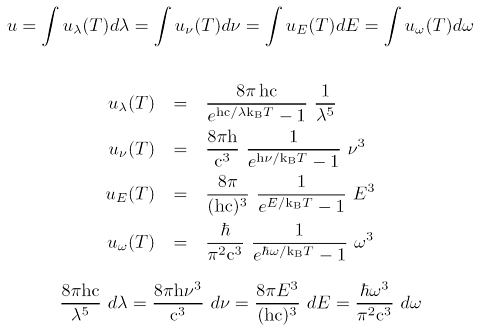
Hier muss man auf die Vorfaktoren aufpassen. Substitution der Wellenlänge durch eine Frequenz involviert andere Vorfaktoren, damit u bzw. alles unter dem Integral immer die Dimension Energie pro Volumen haben. Als Rechenhilfe zeigt die letzte Zeile die Umrechnungen, die sich aus den Substitutionen im Integral ergeben.

Stefan-Boltzmann-Gesetz

Das oben gezeigte Integral für die gesamte Energiedichte u lässt sich explizit ausführen (Verwendung von Gamma- und Zeta-Funktion) und führt auf das berühmte Stefan-Boltzmann-Gesetz oder T⁴-Gesetz. Es besagt, dass die Energiedichte eines Photonengases (ebenso wie dessen Druck und innere Energie) proportional zur vierten Potenz in der Temperatur ist. Die Proportionalitätskonstante heißt Stefan-Boltzmann-Konstante mit dem Zahlenwert σ = 5.67 × 10^-8 W m^-2 K^-4. Diese Relation wurde 1879 empirisch von dem österreichischen Physiker Josef Stefan (1835 – 1893) gefunden und fünf Jahre später von seinem Landsmann Ludwig Boltzmann (1844 – 1906) theoretisch hergeleitet.
Dass der Druck eines Photonengases (radiativer Druck) so stark mit der Temperatur ansteigt, ist bedeutsam für die Stabilität von Sternen in der Astrophysik (siehe auch hydrostatisches Gleichgewicht).

Rayleigh-Jeans- und Wien-Ast

Es ist auch interessant sich zu überlegen, was mit der Planckschen Strahlungsverteilung im Grenzwert großer Wellenlängen (kleiner Frequenzen) bzw. kleiner Wellenlängen (großer Frequenzen) geschieht. Mit den Reihenentwicklungen der Exponentialfunktion folgen dann die beiden wichtigen Grenzfälle, die bei kleinen Frequenzen Rayleigh-Jeans-Ast und bei großen Frequenzen Wien-Ast heißen:

Rayleigh-Jeans-Formel und Wiensche Strahlungsformel sind demnach verschiedene Limites der Planckschen Strahlungsformel. Historisch war gerade das Rayleigh-Jeans-Gesetz (erste Gleichung) der Ausgangspunkt für Max Plancks bahnbrechende Entdeckung. Die Gleichung macht Probleme bei hohen Frequenzen, weil sie dann gegen unendlich strebt. Dieses Verhalten bezeichnen Physiker als Ultraviolettkatastrophe oder Ultraviolettdivergenz.
Plancks Quantisierungsansatz der Wärmestrahlung bereinigte diese UV-Divergenz. Anhand der zweiten Gleichung für den Wien-Ast sieht man wieso: der Exponentialterm dominiert bei großen Frequenzen und 'dämpft' damit die Divergenz ab.
Die Forderung nach Quantisierung läutete eine Vielzahl wichtiger Entdeckungen und Anwendungen in der modernen Physik des 20. Jahrhunderts ein, von der wir heute noch profitieren.

Hochenergetische Wärmestrahlung

Abschließend betrachten wir noch ein Beispiel, das demonstriert, dass Wärmestrahlung nicht immer Infrarotstrahlung sein muss. Dazu verwenden wir die Gleichung der spektralen Energiedichte in Abhängigkeit von der Energie und stellen die Verteilung für verschiedene recht hohe Temperaturen von tausend bis eine Million Kelvin dar (siehe Abbildung oben).
Wie beim Strahlungsmaximum besprochen, bestimmt die Temperatur die Position des Maximums. Ist es denkbar, dass ein Körper so heiß ist, dass seine Plancksche Strahlungsverteilung vor allem im hochenergetischen Röntgenbereich emittiert? Ja, das zeigt uns ein Blick auf die Energieachse im Diagramm: einige keV sind gerade typische Energien der Röntgenstrahlung. Solche Planck-Strahler sind wichtig in der Röntgenastronomie. So ist das intergalaktische Medium (IGM) in Galaxienhaufen so heiß, dass seine thermische Emission typischerweise mit Röntgenteleskopen beobachtet wird.