Das Roche-Volumen (auch Roche-Fläche) ist eine charakteristische Größe in der Diskussion von Doppelsternsystemen (Binären, engl. binaries). Benannt wurde sie nach dem französischen Astronomen Edouard Albert Roche (1820 – 1883), der sich in seinen Forschungen vornehmlich mit den Saturnringen beschäftigte.

Schwer- und Zentrifugalkräfte

Das Roche-Volumen gibt das maximale Volumen eines Sterns an, bevor seine Masse auf den Begleiter überfließen kann. Genauer gesagt gibt es zwei Roche-Volumina in einem Binärsystem – für jeden Stern eines. Normalerweise hält ein Stern seine Masse durch die Gravitationskraft fest. Ist nun ein vergleichbar schwerer Begleiter in der Nähe, wird das Gravitationsfeld gestört: In der Umgebung der Sternmassen gibt es Punkte, wo sich die Gravitationskräfte gegenseitig aufheben. Diese Punkte heißen Lagrange-Punkte benannt nach dem französischen Mathematiker Joseph-Louis Lagrange (1736 – 1813). Die klassische Mechanik behandelt diese Aufgabe als Zwei-Körper-Problem. Es muss dazu gesagt werden, dass die beiden Sterne nicht statisch im Raum liegen, sondern umeinander kreisen. Bei der Betrachtung darf man deshalb Zentrifugalkräfte nicht vergessen. In der Theorie spricht man deshalb von effektiven Gravitationskräften, die um Zentrifugalterme korrigiert sind.

Berechnung im Schwerpunktsystem

Zur Bestimmung der Roche-Volumina muss man sich das effektive Gravitationspotential dieser zwei Sternmassen beschaffen. Historisch ist diese Rechnung schon lange bekannt und kann beispielsweise bei Zdenek Kopal in den Annalen der Astrophysik nachgelesen werden (An. Ap. 18, 379, 1955). Es ist sinnvoll, die Verhältnisse im Schwerpunktsystem zu beschreiben. Man führt also eine Schwerpunktkoordinate und eine Relativkoordinate ein. Das resultierende Gesamtpotential ist als Potentialgebirge in der ersten Abbildung dargestellt (große Version).

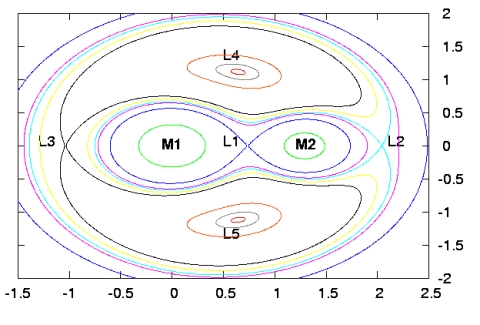
Orte gleichen effektiven Potentials

Man diskutiert das Potential, indem man Linien konstanten Potentials betrachtet. Einige dieser Isokonturlinien des Potentials sind unter das Gebirge projiziert worden. Die zweite Abbildung zeigt die Visualisierung der Isokonturlinien als zweidimensionales Diagramm. Diese so genannte Äquipotentiallinienstruktur zeigt charakteristische Punkte. Es handelt sich dabei um genau fünf Lagrange-Punkte in einem System von zwei Massen, M1 und M2. Sie sind im Diagramm von L1 bis L5 durchnummeriert. Die dreidimensionalen Roche-Volumina der Sterne entsprechen in der Isokonturliniendarstellung der blauen liegenden Acht. In dieser Berechnung wurde angenommen, dass die Masse M1 der Sonnenmasse und die Masse M2 nur einer halben Sonnenmasse entsprechen. Der Abstand der beiden Schwerpunkte M1 und M2 sei gerade so groß wie 1.3 Sonnenradien. Die beiden Raumachsen sind gerade in Einheiten des Sonnenradius beschriftet. Der interessante Punkt in der Ableitung der Roche-Flächen ist nun der innere Lagrange-Punkt L1. Er liegt genau auf der Verbindungslinie der beiden Massenschwerpunkte, zwischen den beiden Massen, am Kreuzungspunkt der Acht. Bei diesen Parametern liegt L1 näher bei der kleineren Masse M2. Das ist plausibel, muss ein Testteilchen doch viel näher an den leichteren Stern kommen, damit ein Gleichgewicht der Kräfte herrscht. Die Lagrangepunkte L2 und L3 liegen hinter den Sternen, jedoch ebenfalls auf der Verbindungslinien der beiden Massenschwerpunkte. Es gilt: L1, L2 und L3 sind kollinear. L4 und L5 sind hingegen außerhalb, bei diesen speziellen Parametern mehr als ein Sonnenradius von L1 entfernt.
Die Roche-Volumina sind nun gerade diejenigen (nicht kugelsymmetrischen!) Volumen, die die blaue Äquipotentialfläche im Dreidimensionalen umschließt und die durch den inneren Lagrange-Punkt verläuft. Im Prinzip ähnelt sie zweien an der Spitze zusammen geklebten Tropfen.
Anhand des Potentialgebirges ist anschaulich klar, dass die Lagrange-Punkte labile Gleichgewichtslagen darstellen. Die Tangenten verlaufen hier horizontal. Tangenten entsprechen gerade der effektiven Kraft, denn der negative Gradient des Potentials ist die Kraft!

Strom kreuzt Roche-Volumen

Sterne sind dynamische Objekte und können sich im Verlauf ihres Sternlebens stark verändern. Die Pulsationsveränderliche sind Sterne, die ihren Sternradius periodisch ändern. Übersteigt nun bei einer Pulsation ein Stern im Binärsystem sein Roche-Volumen, so kann Materie dieses Sterns durch L1 zum Begleiter überfließen. Die Fachwelt nennt dieses Phänomen Roche lobe overflow. Lobe, dt. 'Einhüllende', ist an sich die bessere Begriffswahl anstelle von 'Volumen' oder 'Fläche'. Das Sternplasma strömt dabei nicht auf direktem Wege über, weil der Stern rotiert und deshalb auch das Sternplasma Drehimpuls besitzt. Es kommt zur Ausbildung eines Akkretionsflusses um den Begleiter, z.B. einer Standardscheibe.
Es kann auch vorkommen, dass beide Sterne des Systems ihr Roche-Volumen ausfüllen. Das System hat dann eine hantelförmige Gestalt. In diesem Fall sprechen die Astronomen von Kontaktsystemen. Das Roche-Volumen ist besonders relevant im Verständnis einiger enger Röntgendoppelsterne.

Anmerkung zum Erde-Mond-System

Die hier dargestellten Verhältnisse sind sehr allgemein und auch auf das Erde-Mond-System übertragbar. Würde die Erde den inneren Lagrange-Punkt dieses Systems überschreiten, so würde wahrscheinlich das Wasser der Ozeane zu unserem Trabanten überfließen. Glücklicherweise ist die Erdoberfläche weit genug von L1 entfernt.
Die Lagrange-Punkte des Erde-Mond-Systems haben allerdings eine wichtige praktische Anwendung in der Raumfahrt: Weil diese ausgezeichneten Punkte aufgrund verschwindender effektiver Kräfte relativ stabil sind, positioniert man dort Satelliten, die z.B. astronomische Observatorien tragen. Lagrange-Punkte sind geeignete Satelliten-Parkplätze.