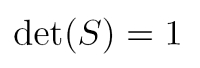Neben Unitarität und Orthogonalität eine bestimmte Eigenschaft von Transformationsmatrizen – oder allgemein gesprochen von Operatoren. Operatoren sind für die Quantentheorie das, was die Tensoren für die Allgemeine Relativitätstheorie sind. Operatorgleichungen wie beispielsweise die Schrödinger-Gleichung legen die Eigenschaften und die Dynamik von Quantensystemen fest. Häufig können physikalische Operatoren als Matrizen, eine Anordnung von (reellen oder komplexen) Zahlen oder auch Funktionen, dargestellt werden. Matrizen haben bestimmte mathematische Eigenschaften. Eine davon ist, dass spezielle Matrizen (gemeint: Matrizen mit der Eigenschaft Spezialität) einen Wert von 1 für ihre Determinanten haben.
Die Transformationen, die diese Matrizen bewerkstelligen, können Gruppen oder Symmetriegruppen bilden und sind dann besonders wichtig in der Gruppentheorie der Physik, wie sie besonders in der Teilchenphysik angewandt wird.
Die (Matrizen-)Eigenschaften Unitarität, Orthogonalität und Spezialität dienen dann einer Klassifikation dieser Gruppen. Details werden unter dem Eintrag Gruppe und Symmetriegruppe besprochen.