Die Stringtheorie (engl. string theory) ist eine Theorie, die Elementarteilchen und die zwischen ihnen wirkenden Kräfte beschreibt. Dabei zielt sie insbesondere auf eine Unifikation ab, d.h. es wird der Versuch unternommen, die fundamentalen Naturkräfte in einem einheitlichen Bild zu beschreiben. Weil dabei auch die Gravitation sowie die Quantisierung berücksichtigt werden, ist die Stringtheorie auch eine Variante einer Quantengravitation.

Warum String?

Etymologisch geht die Bezeichnung Stringtheorie (engl. string: Saite) darauf zurück, dass in der Theorie zunächst nur eindimensionale, fadenförmige Gebilde eine besondere Rolle spielten. Das Anregungsspektrum dieser schwingungsfähigen Objekte wurde mit den bekannten Elementarteilchen des Standardmodells in Verbindung gebracht: je nach Schwingungszustand sollte der String ein bestimmtes Teilchen repräsentieren.

Geschichtliches

Die Entwicklung der Stringtheorien war historisch betrachtet nicht geradeaus, sondern – wie bei der Quantentheorie auch – sprunghaft und über Umwege. Die Forschung dauert an, und so werden immer wieder neue Erkenntnisse zu den Stringtheorien veröffentlicht. Die Stringtheorien wurden in den 1960er Jahren bei der Diskussion der Streumatrix-Theorie motiviert, enthalten aber auch wesentliche Erkenntnisse, die die Kaluza-Klein-Theorie bereits in den 1920er Jahren offen legte – so z.B. die Kompaktifizierung.
Die historische Urform der Stringtheorie ist die bosonische Stringtheorie. Sie wurde Ende der 1960er und in den 1970er Jahren entwickelt, um die starke Wechselwirkung mit quantenmechanischen Strings zu beschreiben. Diese Theorie hat 26 Dimensionen, 25 Raum- und eine Zeitdimension! Diese Stringtheorie beschreibt nur Bosonen und damit vor allem die Kräfte in der Natur, die durch Bosonen vermittelt werden. Fermionen (z.B. Elektronen, Quarks und Neutronen sind Fermionen) sind leider nicht enthalten. Eine weitere Unzulänglichkeit ist, dass die bosonische Stringtheorie Teilchen mit imaginärer Masse hervorbringt, die Tachyonen. Solche Teilchen wurden nie beobachtet und würden fundamentale Probleme in der Physik hervorrufen, z.B. mit der Kausalität. All diese Probleme der bosonischen Stringtheorie einerseits und die Erfolge der Quantenchromodynamik bei der Beschreibung der starken Wechselwirkung andererseits, führten schließlich zur Aufgabe dieser ersten Version der Stringtheorie.
Die 1970er Jahre waren ausgezeichnet durch die Vermutung, dass die Stringtheorien alle vier Wechselwirkungen in der Natur vereinigen könnten – siehe auch Vereinheitlichung. Eine überraschende Entdeckung war, dass in den Stringtheorien so genannte Spin-2-Anregungen (Tensorbosonen) auftraten, die die Physiker gerade mit dem Austauschquant der Gravitation, dem (hypothetischen) Graviton, in Verbindung bringen. Anfangs hatten die Stringtheorien oft phänomenologische und semi-klassische Grundzüge, aber auch der Formalismus der erfolgreichen Quantenfeldtheorien wurde benutzt. Mitte der 1980er Jahre stellte sich heraus, dass nicht nur Strings als Fäden, sondern auch höherdimensionale Objekte möglich sind. Diese Gebilde wurden von Paul Townsendp-Branen mit einer Dimension p getauft. Der Wortbestandteil Bran nimmt Bezug auf Membran, also ein flächenhaftes, schwingfähiges Objekt. Bei verschwindender Dimension, p = 0, hat man es mit einer 0-Bran zu tun, einem Punktteilchen; eine 1-Bran entspricht dem wohl bekannten, eindimensionalen String; die 2-Bran ist eine zweidimensionale Fläche, die man Membran nennt usw.
1997 fand Juan M. Maldacena die so genannte AdS/CFT-Korrespondenz (dazu später mehr), die völlig neue Erkenntnisse über die Zusammenhänge von Gravitation und Teilchenphysik offen legte und zu aktiver Forschung in den Stringtheorien anregte.
Moderne Teilchenbeschleuniger wie der Relativistic Heavy Ion Collider (RHIC) in den USA und der Ende 2007 startende Large Hadron Collider (LHC) am CERN liefern wichtige, experimentelle Daten, die u.a. mit Prognosen der Stringtheorien verglichen werden können.
Die Stringtheorien haben auch Einzug in die Astronomie gehalten. Dort bieten sie interessante Szenarien für Materie unter extremen Bedingungen, z.B. im Innern von kompakten Objekten an. In der Kosmologie wurden stringtheoretische Modelle vorgeschlagen, die unser Universum in völlig neuem Licht erscheinen lassen.

Die Stringtheorie oder die Stringtheorien?

Bis etwa Mitte der 1990er Jahre kannten die Theoretiker eine 26D bosonische Stringtheorie und fünf verschiedene, zehndimensionale Stringtheorien. Damit ist eine Formulierung wie '...das basiert auf den Stringtheorien.' ebenfalls in Ordnung. In den Stringtheorien wurde eine in der Physik sehr vertraute Methode ausgenutzt, die Störungstheorie heißt. Mit diesem mathematischen Apparat konnten physikalisch relevante Aussagen getroffen werden.

neue Sicht auf elementare Bausteine der Materie

Die Sichtweise des Standardmodells, dass die fundamentalen Bausteine der Materie, Quarks und Leptonen, punktförmig seien, wird in der Stringtheorie dadurch abgelöst, dass alle Teilchen als Anregungs- oder Schwingungszustände eines solchen Strings angesehen werden. Dabei ist die Schwingungsenergie des Strings assoziiert mit der Masse des Teilchens. Die Nullpunktsschwingung, die man mit dem Grundzustand der Quantenmechanik identifiziert, entspreche einem Teilchen mit Masse Null. Dies seien gerade die masselosen, bosonischen Austauschteilchen (Eichbosonen) wie das Photon, die Gluonen oder das Graviton. Angeregte Schwingungsmoden repräsentieren Teilchen höherer Masse, wie Elektronen, Neutrinos und Quarks. Die unteilbaren Konstituenten der Materie sind gemäß der Stringtheorie winzige schwingende Fäden oder Flächen auf der Planck-Längenskala (10^-35 m).

verschiedene Typen von Strings

In der String-Topologie unterscheidet man geschlossene Strings (engl. closed strings) von offenen Strings (engl. open strings). Das Graviton und skalare Felder (z.B. das Dilaton) werden durch geschlossene Strings repräsentiert, während die anderen Eichbosonen offene Strings sind. Die Abbildung oben illustriert die topologisch verschiedenen Strings unten und zeigt darüber die zeitliche Entwicklung dieser Strukturen in einem Raum-Zeit-Diagramm. In der zeitlichen Entwicklung erscheint das Punktteilchen (0-Bran) als Linie (links), während die offenen oder geschlossenen Strings (1-Branen) flächenhaft erscheinen (Mitte und rechts).

Die fünf Stringtheorien

Die Terminologie der Stringtheorien definierte seit etwa Mitte der 1980er Jahre folgende fünf verschiedene, zehndimensionale Stringtheorien:

• Typ I,
• Typ IIA,
• Typ IIB,
• O-heterotisch oder SO(32)
• und E-heterotisch oder E₈ × E₈.

Typ I

Die Stringtheorie Typ I behandelt offene und geschlossene Strings. Typ I Strings sind nicht orientiert und elektrische Isolatoren. Offene Strings haben Ränder, auf denen sie elektrische Ladungen tragen. Bei den offenen Strings fixiert man an den Enden Randbedingungen vom Dirichlet-Typ (wie bekannt aus der klassischen Elektrodynamik), daher nennt man sie auch D-Brane. Die Typ I Stringtheorie ist wohl eine äquivalente Formulierung der schwachen Wechselwirkung.

Typ IIA und IIB

Diese beiden Stringtheorien behandeln ausschließlich geschlossene Strings. Typ IIA und IIB Strings sind elektrische Isolatoren. Der Unterschied zwischen Typ IIA und IIB besteht darin, dass Typ IIA keine Orientierung der Strings aufweist, aber Typ IIB hingegen schon. Weiterhin ist die Eichsymmetrie von Typ IIA eine U(1)-Gruppe, wohingegen Typ IIB keine Eichsymmetrie hat.

O-heterotisch und E-heterotisch

Diese heterotische Stringtheorien beschreiben auch nur geschlossene Strings, die orientiert und supraleitend sind. Der Unterschied der beiden besteht in der Eichgruppe: sie heißt SO(32) bei der O-heterotischen Stringtheorie, aber sie heißt E₈ × E₈ bei der E-heterotischen Stringtheorie.
Die beiden heterotischen Stringtheorien bilden sich aus Kombination von Typ II Stringtheorien und bosonischen Stringtheorien. Die Erweiterung auf fermionische Strings gelang im Ramond-Neveu-Schwarz-Modell, kurz RNS-Modell genannt. In diesem Modell erweiterten die Theoretiker die Polyakov-Wirkung, die Strings auf gekrümmten Hintergrundmetriken beschreibt so, dass die Weltfläche eine lokale Supersymmetrie aufweist. Wie gewohnt, führen Wirkungsfunktionale oder alternativ Lagrangedichten, die man ansetzt auf Bewegungsgleichungen (Feldgleichungen). Deren Lösungen sind mit Feldern assoziiert, die gerade bestimmte Teilchen repräsentieren. Die RNS-Wirkung liefert gerade solche Lösungen, die man Majorana-Weyl-Spinoren nennt. An diese offenen oder geschlossenen Strings kann man Randbedingungen stellen. Eine Vorzeichenwahl legt dann Ramond-Randbedingungen (R-Randbedingungen) oder Neveu-Schwarz-Randbedingungen (NS-Randbedingungen) fest. Der Hilbert-Raum hat dann einen R-Sektor und einen NS-Sektor. Die sich ergebenden Wellenfunktionen sind mit Fourier-Koeffizienten gewichtet und können mit Bosonen (symmetrische Zustände) bzw. Fermionen (antisymmetrische Zustände) identifiziert werden.

Superstringtheorien: supersymmetrische Stringtheorien

Alle fünf Stringtheorien sind supersymmetrisch. Aus diesem Grund heißen sie auch Superstringtheorien. Supersymmetrie (SUSY) vermeidet die oben erwähnten tachyonischen Anregungszustände, die zu Akausalitäten führen.
SUSY herrscht zwischen zwei Teilchengruppen: den Bosonen und den Fermionen. Jedes Boson habe einen fermionischen Superpartner, und jedes Fermion habe einen bosonischen Superpartner. Das habe zur Konsequenz, dass weit mehr Teilchen existieren müssen, als im Standardmodell bekannt sind. So hätte das bosonische Graviton den fermionischen Superpartner Gravitino oder die Eichbosonen als Superpartner fermionische Gauginos (Beschreibung der Suffixe unter SUSY). Alle diese supersymmetrischen Partner haben relativ große Massen. Deshalb wurden sie bisher in Teilchenbeschleunigern oder anderen Experimenten nicht entdeckt. Beunruhigend ist in der Tat, dass bisher kein einziges SUSY-Teilchen experimentell nachgewiesen wurde – weder direkt, noch indirekt! Nur die Beobachtung, dass die Kopplungskonstanten der vier Wechselwirkungen, die gewissermaßen ein Maß für die Stärke der jeweiligen Kraft ist, energieabhängig sind und sich zu hohen Energien einander nähern, weist auf die Existenz der SUSY hin.

Was leisten die Stringtheorien?

• Jede der fünf Stringtheorien enthält die Gravitation, d.h. es gelingt eine Beschreibung der Gravitation auf der Quantenebene (Quantengravitation).
• Die Stringtheorien sagen eine supersymmetrische Natur voraus. Bislang wurde diese Eigenschaft nicht experimentell bestätigt, aber falls das der Fall sein wird (eventuell schon bald in modernen Teilchenbeschleunigern), würde das sehr für die Superstringtheorien sprechen. SUSY wird von den meisten Teilchenphysikern als vernünftige Erweiterung des Standardmodells der Teilchenphysik betrachtet.
• Mit den Stringtheorien können Berechnungen im Regime starker Kopplung der Quantenchromodynamik durchgeführt werden, wo die Störungstheorie der herkömmlichen Feldtheorien versagt. Mit diesen QCD-Strings können beispielsweise die experimentellen Daten von Gold-Gold-Stößen, die am Teilchenbeschleuniger RHIC gemessen wurden, sehr gut erklärt werden.
• Ende der 1990er Jahre wurde im Rahmen der Stringtheorien eine der wichtigsten Erkenntnisse der theoretischen Physik in jüngster Zeit gefunden: die so genannte AdS/CFT-Korrespondenz. Diese Korrespondenz besteht zwischen einer Stringtheorie auf einer 5D Anti-de-Sitter-Raumzeit (abgekürzt AdS), die die Gravitation berücksichtigt und einer konformen Feldtheorie (engl. conformal field theory, abgekürzt CFT) ohne Gravitation, die nur auf dem 4D Rand operiert. Die 5D-Strings vermögen nun eine Reihe der Eigenschaften der 4D-QCD (Yang-Mills-Theorie) zu beschreiben. Es ist sogar gelungen, diese Dualität für andere Raumzeiten zu verallgemeinern: sie gestaltet sich dann als eine fundamentale Dualität zwischen Eichung und Gravitation (gauge/gravity dual).
• Mit den Methoden der Stringtheorien lässt sich die Bekenstein-Hawking-Entropie berechnen. Das Resultat stimmt mit demjenigen der klassischen Theorie Schwarzer Löcher überein. Diese Parallele allein besagt nicht viel; aber es lassen sich äußerst interessante Analogien zwischen Quantenchromodynamik und Schwarzen Löchern ziehen: So entspreche ein Übergang in ein Quark-Gluonen-Plasma, wie es die 4D-QCD beschreibt, phänomenologisch der Erzeugung eines Schwarzen Loches in der 5D-Stringtheorie (Maldacena, Nature 423, 695, 2003). Die Bekenstein-Hawking-Entropie klassischer Schwarzer Löcher hängt dann mit der Entropie eines Plasmas aus Quarks und Gluonen zusammen! Das sind vollkommen neue Einsichten in die Natur.

M-Theorie – mysteriöser Überbau von sechs Theorien

Neben den fünf Stringtheorien kennen die Physiker die davon (scheinbar) unabhängige Supergravitation, die Supersymmetrie und Allgemeine Relativitätstheorie (ART) miteinander verknüpft. Nach 1995 entdeckten die Stringtheoretiker, dass die fünf Stringtheorien miteinander über bestimmte, mathematische Relationen, den Dualitäten, in Zusammenhang stehen (Horava & Witten 1996). Die Forscher vermuteten, dass eine übergeordnete Theorie höherer Dimension existiere, die alle Stringtheorien enthalte: die elfdimensionale M-Theorie. M steht für wahlweise für magic, mystery oder matrix – alles Eigenschaften, die der M-Theorie zugeschrieben werden. Erstaunlicherweise stellte sich heraus, dass die M-Theorie eine weitere Theorie enthält: die ebenfalls elfdimensionale Supergravitation (SUGRA). SUGRA und M-Theorie stimmen bei kleinen Energien überein, d.h. die Supergravitation ist der Niederenergielimes der M-Theorie (Horava & Witten 1996). Die Abbildung oben fasst die fünf Stringtheorien und SUGRA zur M-Theorie zusammen. Bis heute sind nur wenige Eigenschaften der M-Theorie bekannt. Die Stringtheoretiker wissen nur, dass sie

• elfdimensional sei,
• der Supergravitation im Limes kleiner Energien entspreche,
• ihre Objekte, die M-Branen, Strings und p-Branen seien,
• sie nicht perturbativ, also störungstheoretisch nicht zugänglich, sei.

Wenn mindestens zwei Strings miteinander wechselwirken, kommt eine physikalische Größe ins Spiel, die Kopplungskonstante heißt. Die numerische Zugänglichkeit der Stringtheorien hängt empfindlich von dieser Größe ab, weil man den Apparat der Störungsrechnung verwendet. Ist die Kopplungskonstante kleiner als eins, ist eine störungstheoretische (perturbative) Behandlung möglich. Ist sie größer als eins, gibt es in seltenen Ausnahmefällen alternative Methoden. Das gestaltet die Formulierung und experimentelle Verifikation der M-Theorie so außerordentlich schwierig.

Wo stecken die anderen Raumdimensionen?

Eine interessante Frage ist nun, weshalb die sechs zusätzlichen Raumdimensionen, die jede der fünf zehndimensionalen Stringtheorien gegenüber der vierdimensionalen Raumzeit der ART mehr hat, nicht im alltäglichen Leben bzw. in physikalischen Messungen in Erscheinung treten. Antwort: Sie sind 'sehr klein', oder wie Physiker sagen, sie sind kompaktifiziert. Unter Kompaktifizierung versteht man, dass Raumdimensionen auf kleinen Raumskalen 'zusammengerollt' sind. Deshalb bleiben sie in der Regel verborgen. Vorstellen kann man es sich anschaulich so, dass beispielsweise eine gezeichnete Linie, die uns als Betrachter eindimensional erscheint, bei hoher Vergrößerung mit einem Mikroskop weitere Dimensionen offenbart: die Linie erscheint dicker, ausgedehnt und wird zu einem zweidimensionalen Streifen.
In den zehndimensionalen Stringtheorien untersucht man nun bestimmte Unterräume mit weniger als zehn Dimensionen, die flach (engl. flat) oder gekrümmt (engl. curved oder warped) sein können. Dazu gehören die Orbifolds, Mannigfaltigkeiten die singuläre Punkte aufweisen und Calabi-Yau-Mannigfaltigkeiten, die Ricci-flach (der Ricci-Tensor verschwindet) und vom Typ her Kähler-Metriken sind. Diese Unterräume werden von kompaktifizierten Raumdimensionen aufgespannt. Im Allgemeinen kann man alle Stringtheorien und die elfdimensionale Supergravitation in Untermannigfaltigkeiten zerlegen: So entsprechen die Typ II Stringtheorien einer Zerlegung in die zuvor bekannte vierdimensionale Raumzeit und dreidimensionale Calabi-Yau-Mannigfaltigkeit. Die heterotischen Stringtheorien können in die vierdimensionale Raumzeit sowie einer K3-Fläche und einem zweidimensionalen Torus zerlegt werden. Schließlich 'synthetisiert' man die elfdimensionale Supergravitation aus vierdimensionaler Raumzeit, dreidimensionaler Calabi-Yau-Mannigfaltigkeit und einem eindimensionalen Kreis.
Ein Soliton ist ein bestimmter Typus einer Welle, ein Wellenpaket, das sich besonders stabil ausbreitet. Es gibt diese gegenüber Störungen sehr widerstandsfähigen Wellen in vielen Bereichen der Physik, so z.B. sowohl in der Optik (optisches Soliton), als auch in der Akustik und Hydrodynamik (Soliton-Wasserwelle). Alle p-Branen der Stringtheorien, die Solitonen sind, lassen sich als Lösungen einer elfdimensionalen Supergravitation finden.
Die Welt der ART ist vierdimensional. Die anderen sieben Dimensionen der Supergravitation bzw. M-Theorie sind kompaktifiziert. Die neuen Dimensionen bezeichnen die Physiker auch als Extradimensionen, die bisher nicht experimentell nachgewiesen werden konnten. Bei kurzen Abständen erwartet man, dass das Newtonsche Gravitationsgesetz mit seiner typischen r²-Abfall für die Gravitationskraft nicht mehr gültig ist. Dies überprüfen die Physiker in Cavendish-Experimenten und anderen Tests. Bislang fanden sie dabei keine Anzeichen für weitere Raumdimensionen außer den klassischen dreien. Das erklären die Stringtheoretiker so, dass die Extradimensionen auf noch kleineren Abständen kompaktifiziert seien, als in Experimenten getestet werden kann. Die aktuelle Grenze liegt im Bereich von Mikrometern, d.h. der so genannte Kompaktifizierungsradius müsse kleiner sein, als ein Millionstel Meter.
Auch in modernen Teilchenbeschleunigern könnte es möglich sein, die Extradimensionen abzuzählen, nämlich dann, wenn die Experimentatoren dort künstlich ein Schwarzes Loch im Miniformat erzeugen und dessen Zerfall durch Hawking-Strahlung beobachten könnte. Die Stringtheorien könnten erklären (aber sie fordern es nicht zwingend!), falls die fundamentale Planck-Skala reduziert sei und daher Effekte der Quantengravitation bereits auf der TeV-Skala auftreten könnten (TeV-Quantengravitation). Dann würden Teilchenbeschleuniger wie der LHC diese Effekte sichtbar machen können.

String landscape: blühende Landschaften der Stringwelt

Die Formulierung von Stringtheorien auf verschiedenen Calabi-Yau-Räumen kann Spiegelsymmetrien aufweisen, so dass das Studium der einen Stringtheorie etwas über die entsprechende dual gespiegelte Stringtheorie verrät.
Eine generelle Problematik ist, dass es möglich ist, unter einer Vielzahl von Calabi-Yau-Räumen auszuwählen. Daraus folgen jedoch beliebig viele Grundzustände (metastabile Vakua) in den Stringtheorien. Diese enorme Zahl falscher Vakua wird unter dem Begriff Stringtheorie-Landschaft (engl. string theory landscape) zusammengefasst.

neue Schwarze Löcher in Stringtheorien

Es ist sogar möglich, im Branen-Formalismus die klassischen Schwarzen Löcher der ART zu verallgemeinern. Die punktförmigen Schwarzen Löcher wären demgemäß 0-Branen, deren Generalisierungen in Form einer 1-Bran, dem Schwarzen String (engl. black string) und der 2-Bran, der Schwarzen Bran (engl. black brane) existierten. Wie in der Quantenfeldtheorie folgen die Bewegungsgleichungen oder Feldgleichungen oder Euler-Lagrange-Gleichungen aus der angesetzten Lagrangedichte (Lagrangian). Die klassische Hilbert-Einstein-Langrangedichte (notiert in der Gleichung rechts) 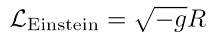führt auf eine Bewegungsgleichung (eom, engl. equation of motion), die das Verschwinden des Ricci-Tensors diktiert. Diese Gleichung hat also Ricci-flache Lösungen, z.B. ungeladene Schwarze Löcher (Schwarzschild-Lösung). Setzt man hingegen die Einstein-Maxwell-Lagrangedichte an, die den Maxwell-Tensor enthält, so findet man Branen-Verallgemeinerungen der klassischen Reissner-Nordstrøm-Lösung.
Eine entsprechende Verallgemeinerung des Ansatzes für den Einstein-Maxwell-Lagrangian in elf Dimensionen führen auf Lösungen, die man pp-Welle (einem bestimmten Typ einer Gravitationswelle) und Taub-NUT-Lösung nennt. Letzteres ist eine nicht-diagonale Metrik, die nicht asymptotisch flach ist. Die seltsame Bezeichnung dieser Vakuumlösung der Einsteinschen Feldgleichungen geht auf die Relativisten zurück, die sie erstmals fanden: A.H. Taub 1951 und in erweiterter Form E.T. Newman, Unti sowie Tamborino 1963. Mit einer 'tauben Nuss' hat diese Lösung nichts zu tun.
Schwarze Löcher können auch durch Schwingungsmoden von 3-Branen repräsentiert werden. Sie tragen dann Masse, elektrische Ladung und Drehimpuls. Damit entspricht dies der Kerr-Newman-Lösung Schwarzer Löcher. Das erstaunliche Ergebnis ist, dass die Stringtheorie exakt die gleiche Entropie vorhersagt, wie sie als thermodynamisches Analogon in der Theorie Schwarzer Löcher gefunden wurde, nämlich die Bekenstein-Hawking-Entropie.
Im Rahmen des D-Branen-Formalismus kann auch die Hawking-Strahlung beschrieben werden: Wechselwirkende offene Strings auf einer D-Brane führen zur Emission von geschlossenen Strings. Diese Behandlung liefert ein so genanntes Graukörper-Spektrum (engl. grey-body spectrum), einer Erweiterung des klassischen Schwarzkörper- oder Planck-Spektrums, das um einen energieabhängigen Absorptionsquerschnitt erweitert ist.

Branenkosmologie

In der modernen, relativistischen Kosmologie werden ebenfalls Konzepte der Stringtheorien angewendet. Ein Modell besteht darin, eine größere Zahl zueinander paralleler Branen auf einer flachen Hintergrundmetrik anzusetzen. Offene Strings gehen an der einen Bran aus und enden an einer anderen. Solche Szenarien laufen unter dem Etikett Stringkosmologie oder Branenkosmologie. Konkrete Beispiele sind das ADD-Szenario und die Randall-Sundrum-Modelle, die großen Anklang in der modernen Kosmologie gefunden haben. Eine besonders spektakuläre Anwendung dieser Form ist das Ekpyrotische Szenario und dessen Erweiterung, das Zyklische Universum (Khoury et al. 2001, Steinhardt & Turok 2001). Diese Modelle liefern sogar eine Erklärung des Urknalls! Jedoch: Sollten sich diese Modelle als richtig erweisen, so stützen sie zwar die Stringtheorie, beweisen jedoch nicht strikt ihre formale Notwendigkeit und Richtigkeit, denn auch eine vierdimensionale Feldtheorie reicht schon als mathematische Basis aus.

Stringtheorien als 'Weltformel'?

Die Physiker suchen nach einer Theory Of Everything (TOE), einer 'Theorie für Alles', die alle vier fundamentalen Wechselwirkungen in einer einheitlichen, theoretischen Sichtweise vereint. Bei der Vereinheitlichung der elektromagnetischen, schwachen und starken Wechselwirkung ist das bereits in Form der Großen Vereinheitlichten Theorien (GUT) gelungen, einer SU(5)-Theorie ohne Strings.
Nur die Gravitation macht ernste Probleme eingebettet zu werden. Die Sonderrolle der Gravitation kann man auch daran sehen, dass in einigen Modellen schwache, starke und elektromagnetische Kraft (also das Standardmodell) nur auf den zehndimensionalen 'Wänden' der elfdimensionalen Welt der M-Theorie existieren, während die Gravitation in der kompletten elfdimensionalen Welt (Bulk) vorherrsche! Viele solcher Bulk-Bran-Systeme wurden vorgeschlagen, die eine Menge interessanter, physikalischer Aspekte bergen – doch keines davon konnte als das Modell für die Natur auserkoren werden. Die Erforschung geht weiter. Die Stringtheoretiker hoffen, dass sie so mehr über die M-Theorie erfahren und die Gravitation als etwas Neues, jenseits der Einsteinschen Theorie, entschleiern.

Kritik an den Stringtheorien

Die aktuelle Forschung auf dem Gebiet der Stringtheorien gestaltet sich so, dass Methoden der Stringtheorien – die nicht nur Strings beschreiben, wie nun klar sein sollte – auf bekannte Probleme der Quantenphysik, Teilchenphysik und Astrophysik angewendet werden. Dies offenbart erstaunliche, neue Perspektiven auf bekannte Phänomene, die oft über den bisherigen Verständnishorizont hinausgehen. Trotzdem bleiben uns die Stringtheorien bzw. die bekannten Facetten der M-Theorie nach wie vor den Beweis schuldig, dass sie konsistente, physikalische Theorien sind. Die ernste Frage ist, ob Stringtheorien wirklich die Natur beschreiben oder eine anspruchsvolle, mathematische Phantasie sind. Kritiker der Stringtheorien werfen ein, dass sie bisher nicht nachweisbare Konzepte, wie die Existenz von Extradimensionen und die Supersymmetrie, verfolgt. Diese Konzepte sind notwendig, um konsistente Stringtheorien (Vermeidung von Tachyonen etc.) zu entwickeln, verweigern sich jedoch bisher hartnäckig jedem experimentellem Nachweis. Diese Einwände sind ernst zu nehmend, berechtigt und mündeten in eine Suche nach Alternativen zu den Stringtheorien.

Alternative zur Stringtheorie

In der so genannten Loop-Quantengravitation (LQG) wurde ein anderer Ansatz gefunden. Der entscheidende Unterschied ist der Folgende: die Stringtheorien folgen quantenfeldtheoretischen Methoden, d.h. Teilchen und Felder werden auf einem Hintergrund, der Raumzeit, betrachtet. Sämtliche Gebilde 'leben' auf dieser Bühne. Die LQG dagegen ist unabhängig von einem Hintergrund. Diese Eigenschaft bezeichnet man mathematisch als (aktive) Diffeomorphismus-Invarianz. Die Hintergrundunabhängigkeit folgt auf natürliche Weise den Prinzipien der klassischen ART, denn hier wird die Raumzeit selbst als deformierbares, dynamisches Gebilde angesehen; in diesem Sinne ist es kein Hintergrund, sondern dynamische Variable. Das hat aber einen hohen Preis: die gewohnten Begriffe von Position und Zeit verlieren ihre Gültigkeit. Die Denkweise der LQG ist anspruchsvoll und neu: sie basiert im Wesentlichen auf Loop-Zuständen, die man sich als Schleifen vorstellen kann. Diese Schleifen formen ein 'Gitter'. Die im Allgemeinen gekrümmte Raumzeit (Sprache der Relativitätstheorie) taucht dann in Form angeregter Zustände (Sprache der Quantentheorie) der Schleifen auf. Das Konzept folgt eher demjenigen der Quantenmechanik, wo ein Hamilton-Operator, die Dynamik des Systems in Form einer Schrödinger-Gleichung festlegt. So wie man das Spektrum des Hamilton-Operators in der quantenmechanischen Behandlung des Wasserstoffsproblems durchführt und die elektronischen Wellenfunktionen sowie Energieeigenwerte gewinnt, kann man in der LQG das Spektrum des Holonomie-Operators berechnen, um die Raumzeit als angeregte Loop-Zustände zu interpretieren.
Die LQG kann allerdings nur eine Alternative zu den Stringtheorien in dem Sinne sein, dass sie eine andere Variante einer Quantengravitation darstellt – die LQG leistet es nicht, alle Naturkräfte zu vereinheitlichen. Schwache, starke und elektromagnetische Wechselwirkung werden in der LQG nicht quantisiert.
Einer der Pioniere auf dem Gebiet der LQG, Carlo Rovelli, hat einen sehr lesenswerten, kritischen Dialog zum Thema 'Stringtheorien vs. Loop-Quantengravitation' verfasst. Er enthält keine Formeln, setzt aber fundierte Kenntnisse auf dem Gebiet der Quantenmechanik, Quantenfeldtheorien und Relativitätstheorie voraus, Titel: A dialog on quantum gravity, hep-th/0310077.
Die LQG liefert einige wohl definierte Resultate, die experimentell getestet werden können. Eine Falsifikation von Vorhersagen der Stringtheorien ist ungleich schwieriger, weil viel Spielraum für alternative Stringmodelle oder andere Parameter besteht. Hier begegnet man Aspekten der Wissenschaftstheorie, wo gefordert wird, dass eine Theorie falsifizierbar, also widerlegbar, sein muss. Ist sie es nicht, so sagt diese Theorie alles und nichts über die Natur aus (die sie ja beschreiben soll) und ist in diesem Sinne unpragmatisch und dogmatisch.
Bei der Reproduktion des Standardmodells der Teilchenphysik tun sich beide Theorien schwer. Hier besteht besonderer Forschungsbedarf. Eine experimentelle Falsifikation von Extradimensionen oder der Supersymmetrie würde die Stringtheorie in arge Bedrängnis bringen, während die LQG ohne diese Konzepte auskommt. Die Antwort liegt also leider in der Zukunft. Stringtheoretiker (stringy people) und Verfechter der Loop-Quantengravitation (loopy people) hoffen, dass entweder die modernen Teilchenbeschleuniger oder kosmologische Beobachtungen die entscheidenden Hinweise bringen werden, die für die eine oder für die andere Theorie sprechen – oder für etwas vollkommen Neues.

Quellenverweise und weitere Informationen

• Horava & Witten: Heterotic and Type I string dynamics from eleven dimensions, Nucl. Phys. B 460, 506, 1996
• Horava & Witten: Eleven-dimensional supergravity on a manifold with boundary, Nucl. Phys. B 475, 94, 1996
• Website von Edward Witten (Princeton, USA)
• Edward Witten: Magic, Mystery, and Matrix, populärwissenschaftlicher Artikel, 1998
• Website zur Superstringtheorie
• Carlo Rovelli: A dialog on quantum gravity, hep-th/0310077
• Vortrag im Wissensportal: An introduction to Brane World Cosmology (Stand März 2004)