Lexikon der Astronomie: Tensoren
Tensoren sind mathematische Größen, die auf geometrischen Objekten, dem n-dimensionalen Raum oder auf Mannigfaltigkeiten, durch ihre Transformationseigenschaften definiert sind. Tensoren sind in vielen Bereichen der mathematischen Physik von großer Wichtigkeit. Die Elastomechanik kennt den Spannungstensor, die Hydrodynamik den Viskositätstensor und die klassische Mechanik den Trägheitstensor. Besonders wichtig werden die Tensoren vor allem in der Allgemeinen Relativitätstheorie (ART), einer Gravitationstheorie, die Albert Einstein 1916 veröffentlicht hat. Nach einer kurzen Einführung in die Tensorterminologie, die Tensoralgebra und die Tensoranalysis wollen wir uns in diesem Eintrag besonders den Tensoren der ART zuwenden.
Tensorstufe und Tensordefinition
Genauso wie Treppen haben Tensoren eine Stufe, nur meint es die 'Anzahl ihrer Indizes' (in der Indexschreibweise). Tensoren unterscheiden sich von Stufe zu Stufe durch ihr Koordinatentransformationsverhalten. Was damit gemeint ist, kann kaum prosaisch ausgedrückt werden, sondern nur präzise in der mathematischen Sprache, nämlich in Form der oben dargestellten Gleichungen.
Anhand von Beispielen wird klarer, was gemeint ist: Tensoren 0. Stufe sind Skalare ('Zahlen'), Tensoren 1. Stufe sind die Vektoren, Tensoren 2. Stufe können als Matrizen mit Zeilen und Spalten dargestellt werden, wie man sie aus der Linearen Algebra kennt. Alle diese Gebilde sind Zahlentupel ('Anordnungen von Zahlen'), und so ist allgemein ein Tensor der Stufe k in einem n-dimensionalen Raum als ein nk-Tupel darstellbar.
Beispiel: Tensor 2. Stufe
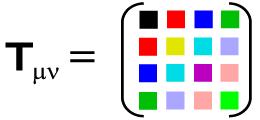Physikalische Tensoren in der ART haben häufig 2. Stufe. Daher sind sie immer als quadratische, symmetrische Matrizen darstellbar. Die Raumzeit der ART ist vierdimensional (n = 4, eine Zeit- und drei Raumdimensionen), so dass Tensoren 2. Stufe als 4 × 4-Matrizen darstellbar sind. Schon ein Tensor 2. Stufe besteht deshalb aus 4 × 4 = 16 Komponenten. Im einfachsten Fall sind die Komponenten Zahlen (z.B. bei der Minkowski-Metrik), im Allgemeinen aber koordinatenabhängige Variablen (z.B. beim metrischen Tensor der Schwarzschild-Metrik). Auf jeden Fall kann man die Komponenten als Anordnung aus vier Spalten und vier Zeilen notieren. Eine solche Anordnung hat eine Hauptdiagonale, die in der ersten Zeile oben links beginnt, über das zweite Element von links in der zweiten Zeile und das dritte Element von links in der dritten Zeile geht und am rechten Element in der vierten Zeile endet (siehe Beispiel rechts). Die Symmetrie besagt nun, dass man an der Hauptdiagonalen spiegeln kann und somit z.B. das Element unten links mit demjenigen oben rechts übereinstimmen muss. In der Abbildung sind farbige Quadrate als Platzhalter für die Tensorkomponenten eingetragen worden. Dabei bedeutet, dass gleiche Farbe den gleichen Tensoreintrag hat. So wird Symmetrie eines Tensors zweiter Stufe unmittelbar anschaulich klar. Denn spiegelt man sorgfältig alle Elemente, so wird klar, dass von den 16 Elementen der symmetrischen Matrix nur 10 übrig bleiben, die wirklich unabhängig voneinander sind.
kovariante und kontravariante Tensoren
Im Tensorkalkül kann man die Stufe eines Tensors verallgemeinern und zwischen kovarianten (Index unten), kontravarianten (Index oben) und gemischten Tensoren (Indizes oben und unten) unterscheiden. Bei gegebenem Tensor unterscheidet sich seine kovariante Form von der kontravarianten darin, dass die Transformationsmatrizen invertiert sind.
Was bedeuteten kovariante und kontravariante Tensoren anschaulich? Betrachten wir eine beliebig gekrümmte Mannigfaltigkeit, die in der ART vierdimensional ist, z.B. eine gekrümmte Raumzeit. Vierdimensional heißt, dass wir die Mannigfaltigkeit durch vier Größen parametrisieren können (z.B. Koordinatenzeit, Radius, zwei Winkel in sphärischen Koordinaten). Dabei handelt es sich also um ein mögliches Koordinatensystem von vielen. Auf diese Weise kann man die Mannigfaltigkeit eindeutig durch ein Linienelement beschreiben. Einfacher vorstellen kann man sich eine zweidimensionale Fläche im dreidimensionalen Raum, z.B. die gekrümmte Fläche eines Globus, den man vor sich ins Zimmer hinstellt. Die zwei Parameter, die die Oberfläche des Globus aufspannen, sind dann beispielsweise zwei Winkel (Längen- und Breitengrad).
Fixieren wir nun einen Punkt P auf dieser Fläche/Mannigfaltigkeit, so kann man sich in jede Koordinatenrichtung durch Bildung der partiellen Ableitung den Tangentenvektor beschaffen. Im Beispiel des Globus zeigen die Tangentenvektoren entlang der Großkreise. Man nennt nun sämtliche kontravariante Vektoren im Punkt den Tangentialraum an P. Im Allgemeinen liegt dieser Raum nicht mehr in der zugrunde gelegten Mannigfaltigkeit. Die Tangentenvektoren im Punkt bilden eine so genannte kontravariante Basis. Demgegenüber besteht die kovariante Basis aus darauf senkrecht stehenden Vektoren (inverse Jacobi-Matrix). Beide Basen eignen sich zur Darstellung von Tensoren und sind gleichwertig. Der metrische Tensor kann benutzt werden, um von einer Darstellung auf die andere zu transformieren.
Tensorterminologie
In der Tensorterminologie nennt man einen Tensor, der i kontravariante Indizes und j kovariante Indizes hat, einen Tensor vom Typ (i,j), seine Stufe ist i+j, also die Summe aller vorhandenen Indizes. Der Tensor Z in der ersten Abbildung hat so beispielsweise den Typ (1,2) und ist Stufe 3.
Einsteinsche Summenkonvention
Die Stellung von Indizes kann man je nach Anforderung des tensoralgebraischen Problems durch Multiplikation mit dem metrischen Tensor anpassen (siehe Beispiele in zweiter Abbildung, rechts). Dabei ist immer die Einsteinsche Summenkonvention zu beachten:
Über wiederholt auftretende Indizes wird summiert.
Und zwar durchlaufen üblicherweise griechische Indizes alle vier Dimensionen der Mannigfaltigkeit (0,1,2,3; 0: Zeit) und lateinische Indizes nur die drei Raumdimensionen (1,2,3). In der Literatur gibt es für die Handhabung der griechischen und lateinischen Buchstaben aber auch Unterschiede, die jedoch zu Beginn vereinbart werden. Die Summenkonvention allerdings ist fundamental und erspart die aufwendige Notation mit Summensymbolen.
Kontraktion oder Verjüngung
Die Stufe eines Tensors kann man auch erniedrigen: dies nennt man Kontraktion. Darüber hinaus existiert im Tensorkalkül auch ein indexfreier Zugang, der in der Anwendung auf ein konkretes Problem weniger praktisch ist.
Weshalb brauchte Einstein Tensoren?
Die Verwendung von Tensoren in der ART ist kein Zufall, denn gemäß des Prinzips der Kovarianz müssen die relativistischen Gleichungen notwendigerweise tensoriell sein. Die Transformationsgesetze der Tensoren (siehe erste Abbildung) lassen schnell erkennen weshalb: Angenommen zwei Tensoren stimmen in einem bestimmten Koordinatensystem (ohne Beschränkung der Allgemeinheit im ungestrichenen System) überein. Dann zeigen die Transformationsgesetze sofort, dass auch die Tensoren im gestrichenen System übereinstimmen! D.h. die Tensoren stimmen dann auch in jedem beliebigen anderen Koordinatensystem überein!
Tensorgleichungen sind koordinatenunabhängig.
Die Wahl eines Koordinatensystems erleichtert nur konkrete Rechnungen. In der Praxis sind Tensorgleichungen eine sehr kompakte Notation in der mathematischen Physik, aber für konkrete Rechnungen muss man meist ein bestimmtes Koordinatensystem (man könnte auch sagen: einen Beobachter, eine Tetrade) auswählen.
Tensoren vs. Tensorfeld
Im allgemeinen Sprachgebrauch der Physiker werden Tensoren synonym mit den Tensorfeldern gebraucht. Der subtile, semantische Unterschied besteht darin, dass Tensorfelder auf einem Gebiet definiert sind, in der ART auf einer vierdimensionalen Mannigfaltigkeit. Die Unterscheidung ist die konsequente Verallgemeinerung von Vektor und Vektorfeld der Vektoranalysis. So sind Tensorfelder Zuordnungen von Tensoren gleichen Typs zu jedem Punkt der Mannigfaltigkeit, ebenso wie bei einem Vektorfeld jedem Punkt eines Gebietes ein Vektor zugeordnet wird (Beispiel: Geschwindigkeitsfeld in der Hydrodynamik).
kompakte Gleichungen mittels Tensorschreibweise
Ebenso wie die Vektoren eine sehr kompakte Formulierung in der Newtonschen Theorie der Gravitation erlauben, gestatten die Tensoren der ART eine sehr kompakte, tiefsinnige Darstellung der Einsteinschen Gravitationstheorie: ein ganzer Satz von Differentialgleichungen (zehn gekoppelte, nichtlineare, partielle Differentialgleichungen) kann so als eine Gleichung geschrieben werden, die einen tiefen, physikalischen Gehalt birgt: die Einsteinschen Feldgleichungen offenbaren eine direkte Verbindung von Raumkrümmung, repräsentiert durch den Einstein-Tensor, und Energie bzw. Materie, repräsentiert durch den Energie-Impuls-Tensor!
physikalische Tensornamen in der ART
Tensoren in der relativistischen Physik haben maximal 4. Stufe, wie der Riemannsche Krümmungstensor und Weyl-Tensor. Viele Tensoren können physikalisch anschaulich interpretiert werden. Näheres ist bei den einzelnen Tensoren selbst nachzulesen:
Schreiben Sie uns!