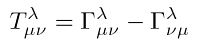Der Torsionstensor ist allgemein definiert als die Differenz zweier metrischer Zusammenhänge, die gerade vertauschte kovariante Indizes haben. Ist diese Differenz endlich, also verschieden von null, so ist eine Torsion ('Verdrillung') der Mannigfaltigkeit vorhanden.

ART ist torsionsfrei

In der Allgemeinen Relativitätstheorie (ART) entsprechen die metrischen Zusammenhänge gerade den Christoffel-Symbolen (Γs in der Gleichung rechts). Gravitationstheorien, die auf dem Äquivalenzprinzip basieren sind, haben symmetrische Christoffel-Symbole. Demzufolge verschwindet der Torsionstensor in der ART, und Relativisten sprechen dann von Torsionsfreiheit der Theorie.

Tensoreigenschaften

Der Torsionstensor ist ein Tensor vom Typ (1,2), also ein Tensor dritter Stufe, während die Christoffel-Symbole selbst keine Tensoren sind. Der Torsionstensor darf nicht mit dem Energie-Impuls-Tensor verwechselt werden, der ebenfalls mit dem Buchstaben T bezeichnet wird. Die unterschiedlichen Tensorstufen mögen als Unterscheidungskriterium dienen. Normalerweise besteht in der ART auch deshalb keine Verwechslungsgefahr, weil der Torsionstensor kaum betrachtet wird, weil er verschwindet.

Hat die Gravitation eine Torsion?

Die Differentialgeometrie kennt sicher Mannigfaltigkeiten, wo das nicht der Fall ist, sie finden aber keine Anwendung in der Relativitätstheorie.
Es gibt aber auch Forscher, die versuchen eine Gravitationstheorie mit Torsion aufzuziehen. Diese Gravitation ist komplizierter, weil neue Zusatzterme auftauchen, die in der ART verschwinden. Bisher gibt für eine Gravitation mit Torsion keine Anhaltspunkte in der Natur.