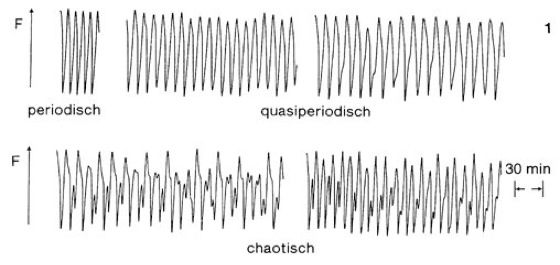
Chaoss [kaos; von griech. chaos = gähnend, leerer Raum]. In der griech. Mythologie, wie sie von Hesiod um 700 v. Chr. aufgezeichnet wurde, steht Chaos für den ungeordneten, "gähnenden" Zustand, mit dem die Welt begann. Auch für den Arzt Paracelsus im 16. Jahrhundert war Chaos die "materia prima", der Urstoff aller Dinge. Wissenschaftler bezeichnen heute mit Chaos einen zeitlichen Ablauf in einem dynamischen System, bei dem sich die Ereignisse nie in gleicher Weise wiederholen, d. h., bei dem keine Periodizität erkennbar ist. Beispiele, die jeder kennt, sind Wellen an der Küste, Flammen im Kamin und das Wetter. Vom Chaos auszuschließen sind sog. quasiperiodische Vorgänge, die zwar auch keine erkennbare Periode zeigen, sich jedoch als Summe von periodischen Vorgängen darstellen lassen. Läßt sich ein chaotisches System mathematisch derart beschreiben, daß aus gegebenen Anfangsbedingungen die zukünftige Entwicklung im Prinzip berechenbar ist, spricht man von "deterministischem Chaos". Da zur Simulation chaotischer Vorgänge leistungsfähige Computer notwendig sind, hat sich die Chaosforschung erst seit Anfang der sechziger Jahre entwickeln können. Um 1889 hatte der franz. Mathematiker Henri Poincaré die Besonderheit solcher Vorgänge erkannt, aber mangels Computer nicht berechnen können. Erst 1963 gelang es dem amerikan. Meteorologen Edward Lorenz bei der Computerberechnung eines stark vereinfachten Wettermodells, diese Vorgänge zahlenmäßig überzeugend darzustellen. In der Biochemie erbrachten 1977 Olsen und Degn (Odense, Dänemark) den ersten Nachweis von Chaos. Sie fanden chaotische Schwingungen in der Reaktion, die durch das Enzym Peroxidase katalysiert wird. Ein zweiter chaotischer biochemischer Prozeß wurde 1984 von Markus, Kuschmitz und Hess (Dortmund) in der Glykolyse beobachtet. Abb. 1 ( vgl. Abb. ) zeigt die Abhängigkeit der Fluoreszenz F des Glykolyse-Intermediats NADH (Nicotinamidadenindinucleotid) bei periodischer, quasiperiodischer und chaotischer Schwingung der "inneren Uhr" (biologische Uhr) der Hefe.
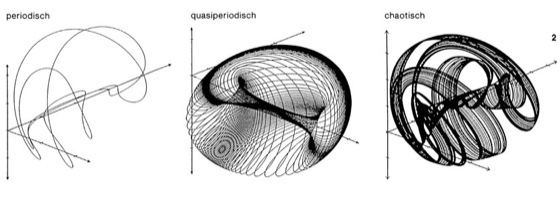
Dynamische Prozesse im allgemeinen lassen sich als Bahnen im sog. Phasenraum darstellen. Dies ist ein Raum, dessen Koordinaten unabhängige Größen sind, welche das System beschreiben (Phasenvariablen). Zum Beispiel sind in einem mechanischen System Phasenvariablen durch Orte und Impulse gegeben, in einem chemischen oder biochemischen System durch die Konzentration reagierender Substanzen. Aus einer einzigen gemessenen Phasenvariablen x in Abhängigkeit von der Zeit t läßt sich ein Phasenraum "rekonstruieren", indem man als zusätzliche Phasenvariablen die zeitlich verzögerten Größen x(t + τ), x(t + 2 τ), x(t + 3τ) usw. (τ ist konstant) einführt. Abb. 2 (vgl. Abb.) zeigt verschiedene Bahnen, wie sie von Markus und Hess für die Glykolyse im Phasenraum der Reaktanden-Konzentration berechnet wurden. Im allgemeinen bestehen periodische Bahnen aus einer geschlossenen Kurve, quasiperiodische Bahnen aus einem Torus und chaotische Bahnen aus einer teilweise raumfüllenden Menge. Ebene Schnitte durch einen Phasenraum nennt man Poincaré-Schnitte. In Schnitten dreidimensionaler Phasenräume erscheinen periodische Bahnen als eine endliche Zahl von Punkten, quasiperiodische Bahnen als geschlossene Kurven und chaotische Bahnen als teilweise flächenfüllende Mengen. Dynamische Systeme lassen sich in konservative und dissipative Systeme unterteilen. Konservative Systeme sind solche, bei denen Energie (und Materie) erhalten bleiben. Beispiele findet man bei einzelnen Teilchen im Vakuum oder bei Himmelskörpern. Da es unendlich viele Energien gibt, gibt es auch entsprechend viele Bahnen im Phasenraum. Abb.3 ( vgl. Abb. ) zeigt einen Poincaré-Schnitt einer Vielzahl von Bahnen in einem konservativen System. Man erkennt Quasiperiodizität (geschlossene Kurven) und Chaos (teilweise flächenfüllend). Im Gegensatz zu konservativen Systemen wird bei dissipativen Systemen (Beispiele sind chemische Reaktionen und biochemische Reaktionen) ständig nutzbare Energie bzw. Materie umgewandelt, so daß ein dynamischer Zustand nur aufrechterhalten werden kann, wenn die Verluste durch entsprechende Zufuhr von außen ausgeglichen werden (dynamisches Gleichgewicht). Dieser Ausgleich kann allerdings nur für ganz bestimmte Phasenraum-Bahnen (Attraktoren genannt) erreicht werden. Bei Anfangsbedingungen, die nicht auf dem Attraktor liegen, durchläuft das System erst sog. Transienten, bis es dann auf dem Attraktor landet. Abb. 4 ( vgl. Abb. ) zeigt einen Poincaré-Schnitt eines sehr langen Transienten der Glykolyse. Dem Attraktor entsprechen hier vier Punkte (die Schnittpunkte einer periodischen Bahn), während alle anderen Punkte durch Transienten zustande kommen. Eine bemerkenswerte Eigenschaft chaotischer Attraktoren ist ihre Fraktalstruktur. Fraktale sind Gebilde, bei denen sich verschieden große Teilgebilde bei entsprechender Vergrößerung ähneln. Man spricht von Selbstähnlichkeit. Näherungsweise sind Bäume ein Beispiel: vergrößert ähnelt ein großer Ast dem ganzen Baum, ein kleiner Ast einem großen Ast usw. Ein anderes Beispiel ist die Oberfläche eines Blumenkohls. Ein einfaches rechnerisches Beispiel ist die sog. Cantor-Menge. Zu ihrer Erzeugung nimmt man aus einem Linienstück das mittlere Drittel heraus, aus den verbleibenden Stücken wieder das mittlere Drittel usw. Wird dieser Vorgang unendlich oft wiederholt, entsteht eine Menge mit unendlich vielen einzelnen Punkten: die Cantor-Menge. Ein Poincaré-Schnitt durch eines der Bänder des Glykolyse-Attraktors (rechter Teil in Abb. 2, [vgl. Abb.]) hat eine ähnliche Struktur wie die Cantor-Menge. Ein in Computerkreisen beliebtes Fraktal ist die Mandelbrot-Menge (auch "Apfelmännchen" genannt), die in Abb. 5 ( vgl. Abb. ) gezeigt wird. Hier sieht man deutlich, wie die kleinen stacheligen "Männchen" bei jeder Vergrößerung vorkommen, etwa wie bei Jonathan Swifts "Flöhe, welche Flöhe hatten, welche Flöhe hatten, usw." Man erzeugt die Mandelbrot-Menge mit der Gleichung z_n+1 = z_n² + c, wobei die z_n (n = 0,1,2,...) komplexe Zahlen sind; z₀ = 0 wird rechts eingesetzt und liefert z₁, z₁ wird rechts eingesetzt und liefert z₂ usw. Jeder dieser Rechenschritte heißt Iteration. Die Mandelbrot-Menge ist die Menge aller komplexen Zahlen c, für welche die Iterationen zu einem endlichen Grenzwert führen.
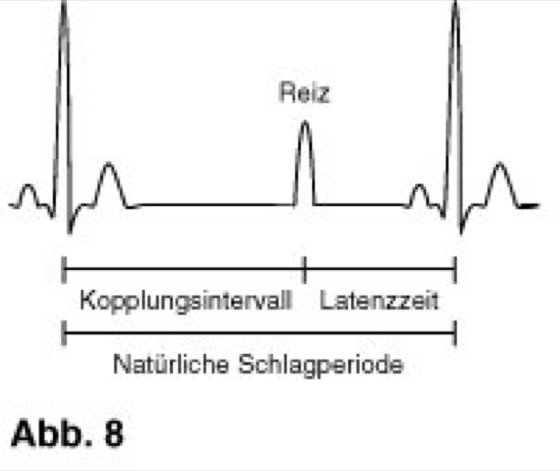
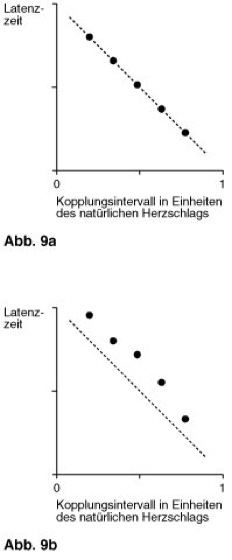
Eine wesentliche Eigenschaft chaotischer Systeme ist ihre Unvorhersagbarkeit, obwohl sie deterministisch durch mathematische Gleichungen beschrieben werden. Diese Eigenschaft rührt daher, daß in diesen Systemen unvermeidbare Ungenauigkeiten (etwa durch Rundungsfehler im Computer oder durch Meßungenauigkeiten) nach einer gewissen Zeit das ganze Geschehen überschatten. Man nennt dies den "Schmetterlingseffekt": der Flügelschlag eines Schmetterlings kann das Wetter im nächsten Urlaub beeinflussen. Zur quantitativen Beschreibung der Unvorhersagbarkeit ist es nützlich, den sog. maximalen Lyapunov-Exponenten ( ^λ_max) zu bestimmen. Im Falle von Chaos ist λ_max positiv und gleich dem Kehrwert der mittleren Zeit, nach der sich eine Ungenauigkeit verdoppelt: ein großes λ_max bedeutet also große Unvorhersagbarkeit. Im Falle von Periodizität ist λ_max negativ, und sein Betrag ist gleich dem Kehrwert der Zeit, nach der eine Abweichung vom Attraktor halbiert worden ist; ein stark negatives λ_max bedeutet in einem solchen Fall starke Erholungsfähigkeit nach einer Störung. – Ein sehr einfaches System, welches Periodizität und Chaos erzeugt, ist die logistische Gleichung x_n+1 = r x_n(1–x_n). Wie bei der Mandelbrot-Menge führt man auch hier Iterationen durch, allerdings mit reellen statt mit komplexen Zahlen. Die logistische Gleichung wurde zur vereinfachten Berechnung von Tierpopulationen (Population) eingeführt, wobei die x_n (n = 1,2,3,...) die Zahl der Tiere darstellen und r ein Parameter ist, der die Umweltbedingungen enthält. Nach Ablauf der Transienten verhält sich die logistische Gleichung wie folgt. Für r zwischen 0 und 3 erhält man einen konstanten Wert. Für r zwischen 3 und 3,44865... schwingt x_n zwischen zwei Werten. Für r zwischen 3,44865... und 3,54413... zwischen vier Werten. Für höhere r-Werte verdoppelt sich die Periode (acht Werte, sechzehn Werte, usw.) in immer kleiner werdenden r-Intervallen (Periodenverdopplungskaskade oder Feigenbaum-Szenario), bis für r größer als 3,56994... (und kleiner als 4) die Periode unendlich groß wird, was nichts anderes als Chaos bedeutet. λ_max berechnet man in diesem Fall als Mittelwert sehr vieler Iterationen des Logarithmus des Absolutwertes der Ableitung von x_n+1 nach x_n, hier gleich r–2rx_n. Möchte man periodisch veränderliche Umweltbedingungen berücksichtigen, so kann man r bei jeder Iteration zwischen zwei Werten A und B wechseln lassen. Dabei ergibt sich Abb. 6 ( vgl. Abb. ), wobei der untere Teil eine Ausschnittvergrößerung des oberen Teils ist. Hier ist λ_max durch Grauwerte in Abhängigkeit von A (x-Achse) und B (y-Achse) dargestellt. Die helleren Partien im (scheinbaren) Bildvordergrund entsprechen Periodizität, der Bildhintergrund entspricht Chaos. Abb. 6 ( vgl. Abb. ) verrät eine Fraktalstruktur mit den in kleinen Ausschnitten immer wiederkehrenden schwalbenähnlichen Motiven. Abb. 7 ( vgl. Abb. ) zeigt das Ergebnis bei periodischem Wechsel zwischen 6 Iterationen mit r = A und 6 Iterationen mit r = B. Eine bemerkenswerte Eigenschaft des deterministischen Chaos ist die Universalität seines Auftretens: von der (Bio-) Chemie, Ökologie, Epidemiologie und Physiologie bis hin zur Astronomie. Hier seien einige noch nicht genannte Beispiele aufgezählt. In der Chemie haben Roux (Bordeaux) und Swinney (Austin, Texas) Chaos bei Oszillationen der Zhabotinsky-Belousov-Reaktion festgestellt. In der Epidemiologie ergeben die Datenauswertungen von Schaffer und Kot (Tucson, Arizona) und von Olsen (Odense, Dänemark), daß die Schwankungen der Zahl der Masernerkrankungen in New York, Baltimore und Kopenhagen (vor dem Beginn der Massenimpfungen) deterministisch-chaotischen Gesetzmäßigkeiten folgen. Im physiologischen Bereich unterscheidet man zwischen pathologischem Chaos (sog. dynamische Krankheiten) und physiologisch nützlichem Chaos. Beispiel des letzteren: Attraktoren, die aus EEG-Signalen (Elektroencephalogramm) rekonstruiert werden, verraten stärkeres Chaos bei gesunden Menschen als bei Patienten während eines epileptischen Anfalls (Epilepsie). Freeman (Berkeley, Kalifornien) vermutet, daß Chaos im Gehirn Lernprozesse ermöglicht: im normalen chaotischen Gewirr von neuronalen Verbindungen werden jene gefestigt, die sich als sinnvoll im Zusammenhang mit neuen Sinneseindrücken und im Kontext des bereits Erlernten erweisen. Ein weiteres Beispiel, bei dem Chaos mit nützlichen Körperfunktionen zusammenhängt, ergibt sich aus den von Hesch (Hannover) untersuchten Schwingungen des Parathormons, welche bei gesunden Menschen chaotischer sind als bei Patienten mit Osteoporose – einer Knochenschwäche, die allein in der Bundesrepublik Deutschland jährlich einen Sozialschaden von mehreren Milliarden DM verursacht. Beispiele von pathologischem Chaos: Schwingungen der Zahl der weißen Blutkörperchen (Leukocyten) bei Patienten mit Leukämie und Herzflimmern beim "Sekundenherztod". Bezüglich des letzteren Beispiels ist allerdings zu beachten, daß Untersuchungen von Goldgerber (Harvard-Universität) gezeigt haben, daß der normale Herzrhythmus (Herzautomatismus) eine kleine chaotische Komponente hat, deren Abklingen ein Vorbote des Todes ist, da vor einem Herzstillstand der Herzrhythmus zunehmend geordneter wird. Somit wäre beim Herzen Gesundheit durch die richtige Balance von Chaos und Ordnung gegeben ( vgl. Infobox ). – In der Astronomie findet man Chaos beim Taumeln des Saturn-Mondes Hyperion, bei den Bewegungen von Saturnring-Brocken mit bestimmten Umlaufzeiten als Ursache der bekannten Trennzonen (z. B. Cassinische Teilung) im Ringsystem sowie auch bei bestimmten Asteroiden (Planetoiden), die ihre Umlaufregion zwischen Mars und Jupiter verlassen und (in seltenen Fällen) als Meteorite auf der Erde landen. König Oskar von Schweden schrieb Ende des 19. Jahrhunderts einen Preis für die Beantwortung der Frage aus, ob die Erde durch den Einfluß anderer Planeten eine stabile Bahn hat. Ohne Computer mußten die Fachleute damals auf eine Antwort verzichten. Erst 1989 konnte Laskar (Paris) mit Hilfe eines Supercomputers das entsprechende λ_max bestimmen. Ergebnis: λ_max für die Erdbahn ist positiv (Chaos!), und sein Kehrwert beträgt etwa 5 Millionen Jahre.
So wie die Computerentwicklungen der sechziger Jahre die Erforschung des Chaos bei zeitabhängigen Systemen ermöglichten, so stehen wir am Ende des 20. Jahrhunderts durch die Entwicklung der Parallelrechner an der Schwelle einer neuen Entwicklung: Chaosforschung bei Systemen, die sich in jedem Punkt eines dreidimensionalen Raumes zeitlich entwickeln, wie sie in den Strömungen von Flüssigkeiten und Gasen vorkommen. Man erhofft sich daraus eine Vertiefung unseres Wissens über Turbulenzen zum Nutzen der Wetterforschung, der Plasmaphysik und der Optimierung von technischen Transportsystemen. Eine noch offene Frage ist z. B., inwieweit durch die heutigen Entwicklungen der Datenverarbeitung eine mathematische Beschreibung chaotischer Körperrhythmen Einzug in das Diagnose-Repertoire der Mediziner halten wird. Chronobiologie, biochemische Oszillationen, biologische Oszillationen, Glykolyse-Oszillator, Symmetrie.

M.M.

Lit.:Jürgens, H., Peitgen, H.O., Saupe, D. (Hrsg.): Chaos und Fraktale. Heidelberg 1989. Lewin, R.: Die Komplexitäts-Theorie. Wissenschaft nach der Chaosforschung. München 1996. Mandelbrot, B.: Die fraktale Geometrie der Natur. Basel ⁵1989. Peitgen, H.O., Jürgens, H., Saupe, D., Maletsky, E.M., Perciante, T., Yunker, L.: Chaos. Iteration, Sensitivität, Mandelbrot-Menge. Ein Arbeitsbuch. Berlin 1992.