komplexe Reaktion, eine chem. Reaktion, die nicht in einem Schritt abläuft. An der Umwandlung der Ausgangs- in die Endstoffe sind mehrere Elementarreaktionen beteiligt. Vielfach werden dabei Zwischenstoffe gebildet und anschließend wieder verbraucht.

Nach der Art der Verknüpfung der Teilschritte unterscheidet man drei Grundtypen k. R.:

1) Gleichgewichtsreaktionen (umkehrbare oder reversible Reaktionen), z. B. A

P;

2) Parallel- (Konkurrenz-) Reaktionen, z. B.

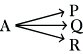
3) Folgereaktionen, z. B. A → B → C.

komplexe Reaktion. Konzentrations-Zeit-Kurven komplexer Reaktionen: (a) Gleichgewichtsreaktion, (b) Parallelreaktion, (c) Folgereaktion. c_Peq und c_Aeq sind Gleichgewichtskonzentrationen.

Diese Grundtypen können auch gekoppelt auftreten:

4) Folgereaktionen mit umkehrbaren Teilschritten, z. B. A + B

C → P + Q;

5) Folgereaktionen mit parallelen Teilschritten, z. B.

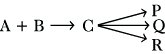
6) konkurrierende Folgereaktionen, z. B.

A + B → P + Q und

A + P → R + S;

7) Parallelreaktionen mit umkehrbaren Teilschritten, z. B.

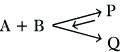
8) geschlossene Folgereaktionen (Kettenreaktionen), z. B.

Katalytische Reaktionen sind stets k. R., da der Katalysator mit den Substraten Zwischenverbindungen bildet (Katalyse). Entstehen in einer Reaktion Produkte, die katalytisch wirken, die Reaktion also beschleunigen oder auch hemmen, spricht man von einer autokatalytischen Reaktion. Derartige k. R. können unter bestimmter Voraussetzung ein anomales Verhalten zeigen (oszillierende Reaktion).

Formalkinetische Behandlung der k. R. Die kinetische Behandlung erfordert die mathematische Beschreibung der zeitlichen Änderung der Konzentrationen c₁ sämtlicher Ausgangs-, Zwischen- und Endstoffe i, die sich aus der Summe bzw. Differenz ihrer Bildungs- bzw. Verbrauchsgeschwindigkeiten in allen Teilschritten j ergibt, an denen sie beteiligt sind, d. h., es gilt

Dabei ist ν_ij der stöchiometrische Faktor für den Stoff i in der j. Reaktion, τ_j die Geschwindigkeit der j. Reaktion. ν_ij ist positiv, wenn der Stoff gebildet, negativ, wenn er verbraucht wird. Für k. R. resultieren komplizierte, meist nichtlineare Differentialgleichungssysteme, die nur in den einfachsten Fällen (z. B. wenn alle Teilschritte 1. Ordnung sind) geschlossen lösbar sind. Einige besonders einfache Fälle sind in der Tab. zusammengestellt. Ist eine geschlossene Lösung nicht möglich, müssen die Gleichungssysteme schrittweise numerisch integriert werden (kinetische Modellierung).

Näherungsverfahren zur Vereinfachung des Differentialgleichungssystems: 1) Wird in einer Reaktion ein reaktives Intermediat gebildet, das sehr schnell weiterreagiert, so liegt es in der Mischung in sehr geringer Konzentration vor. Es kann angenommen werden, daß die Konzentration c_I des Intermediates nahezu konstant ist, d. h. dc_I/dt ≈ 0 (quasistationäre oder Bodenstein-Näherung). 2) Enthält eine k. R. reversible Teilschritte, bei denen die Rückreaktion sehr schnell im Vergleich zu den anderen Elementarschritten erfolgt, kann vorausgesetzt werden, daß diese sich im chem. Gleichgewicht befinden. Die Konzentrationen der Reaktionspartner können angenähert mit dem Massenwirkungsgesetz berechnet werden (Quasigleichgewichtsnäherung). 3) Ist bei einer Folgereaktion ein Teilschritt wesentlich langsamer als die übrigen, dann wird die Bildungsgeschwindigkeit der Produkte und das dafür geltende Zeitgesetz durch diesen Teilschritt bestimmt (Näherung vom geschwindigkeitsbestimmenden Schritt).

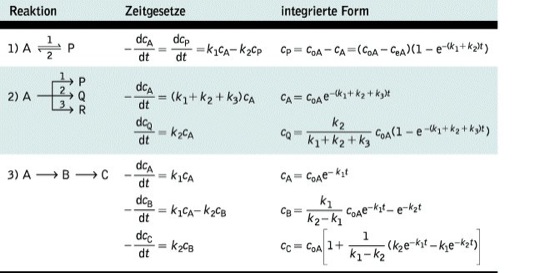
Zeitgesetze der einfachsten Grundtypenk. R. (Tab.): 1) Reversible Reaktion (Abb. 1): Aus dem Zeitgesetz ist das Massenwirkungsgesetz auf kinetischem Wege ableitbar.

2) Parallelreaktion: Gilt für alle parallelen Teilschritte das gleiche Zeitgesetz, dann ist die Bruttogeschwindigkeitskonstante k gleich der Summe der k-Werte für die einzelnen Teilschritte: k = Σ k_i. Sind bei Reaktionsbeginn keine Endstoffe in der Mischung vorhanden, dann ist zu jedem Zeitpunkt das Verhältnis der Produktkonzentrationen gleich dem Verhältnis der Geschwindigkeitskonstanten (Wegscheider-Prinzip; Abb. 2). Das Verhältnis der k-Werte wird auch als Selektivität bezeichnet.

Konkurrieren verschiedene Ausgangsstoffe B, C und D um einen Reaktanten A, dann enthalten die Teilschritte neben c_A die Konzentrationen c_B, c_C oder c_D. Hier gilt das Wegscheider-Prinzip nicht, da die Geschwindigkeiten auch von den frei wählbaren Konzentrationen der Zweitkomponenten abhängen.

3) Folgereaktionen aus zwei Teilschritten 1. Ordnung: Die Konzentration des Zwischenstoffes B geht durch ein Maximum (Abb. 3). An dieser Stelle wird B gleich schnell gebildet und verbraucht. Ist B das Zielprodukt einer Umsetzung, so muß die Reaktion an dieser Stelle abgebrochen werden.

4) Kettenreaktion: Typische Beispiele sind Polymerisationen, radikalische Halogenierungen und Sulfohalogenierungen von Kohlenwasserstoffen, Verbrennungen, Autoxidationen und Pyrolysen vieler organischer Verbindungen. Kettenreaktionen bestehen aus drei Reaktionsstadien: dem Kettenstart, der Kettenfortpflanzung und dem Kettenabbruch. Im Kettenstart werden reaktive Zwischenstoffe, die Kettenträger (z. B. Radikale, Atome, Ionen oder Radikal-Ionen), gebildet. Bei Halogenierungen ist der Start eine thermische oder photochem. Dissoziation des Halogens, z. B. Cl₂

2 Cl·, bei Autoxidationen ein Redoxprozeß unter Beteiligung von Luftsauerstoff, z. B. RH + O₂ → R· + ·O-O-H. Die Reaktion kann auch durch Initiatoren gestartet werden. In der Phase der Kettenfortpflanzung reagiert jeweils ein Kettenträger mit einem Substratmolekül, wobei stets ein neuer Kettenträger zurückgebildet wird, der wieder in die Reaktion eingreifen kann. Die Kette endet durch den Kettenabbruch. Dabei werden Kettenträger vernichtet. Der Kettenabbruch kann bimolekular durch Kombination zweier Radikale oder monomolekular durch Adsorption des Kettenträgers an der Gefäßwand bzw. Reaktion mit einem Stoff, dem Inhibitor, erfolgen, bei dem der Kettenträger in ein wenig reaktives Zwischenprodukt umgewandelt wird. Die Art der Abbruchsreaktion beeinflußt die Form der kinetischen Geschwindigkeitsgleichung entscheidend. Für die Monochlorierung von Kohlenwasserstoffen gilt das einfache Kettenschema

Start: Cl₂ → 2 Cl· (1)

Fortpflanzung: Cl· + RH → HCl + R· (2)

R· + Cl₂ → RCl + Cl· (3)

Abbruch: 2 Cl· → Cl₂ (4)

komplexe Reaktion. Tab.: Zeitgesetze der einfachsten komplexen Reaktionen.

1) Gleichgewichtsreaktion,
2) Parallelreaktion,
3) Folgereaktion; c_oA Anfangskonzentration des Ausgangsstoffes A, c_eA Gleichgewichtskonzentrationen von A, die Anfangskonzentrationen aller Zwischen- und Endprodukte sind 0.

Ein Kettenzyklus besteht aus den Teilschritten (2) und (3). Danach liegt wieder Cl· vor, das erneut gemäß Reaktion (2) mit RH reagieren kann. Zur Ableitung des Zeitgesetzes nimmt man quasistationäre Konzentrationen der Chloratome Cl· und der Alkylradikale R· an. Als Kettenlänge bezeichnet man die Anzahl der Kettenzyklen, die von einem Kettenträger nach seiner Bildung im Startschritt ausgelöst werden, bevor er in der Abbruchsreaktion wieder vernichtet wird. Die mittlere Kettenlänge läßt sich aus dem Quotienten Kettenfortpflanzungsgeschwindigkeit/Startgeschwindigkeit berechnen. Je nach der Art der Kettenreaktion werden Kettenlängen zwischen 1 und etwa 10⁶ beobachtet. Bei Polymerisationen bestimmt die Kettenlänge die Größe des entstehenden Makromoleküls und damit die physikalischen Eigenschaften des Polymeren. Bei photochemisch initiierten Kettenreaktionen resultieren Quantenausbeuten, die wesentlich über eins liegen. Beispielsweise wurden so für die Chlorknallgasreaktion H₂ + Cl₂ → 2 HCl Kettenlängen von 10⁴ bis 10⁵ ermittelt.

Ein besonderer Typ sind verzweigte Kettenreaktionen. Sie werden vor allem bei Verbrennungsreaktionen beobachtet. In den Kettenzyklen sind zusätzlich Verzweigungsschritte enthalten, bei denen aus einem Kettenträger zwei gebildet werden, von denen jeder einen neuen Zyklus einleiten kann. Bei der Knallgasreaktion 2 H₂ + O₂ → 2 H₂O treten z. B. als Verzweigungen die Elementarreaktionen H· + O₂ → ·OH + ·O· und ·O· + H₂ → ·OH + H· auf. Eine weitere Möglichkeit ist der Zerfall instabiler Zwischenprodukte in zwei Radikale (degenerative Verzweigung). So werden z. B. bei der Kohlenwasserstoffoxidation Hydroperoxide ROOH gebildet, die leicht gemäß ROOH → RO· + ·OH thermisch spalten und damit neue Kettenträger bilden. Übersteigt die Bildungsgeschwindigkeit der Kettenträger ihre Vernichtung durch Abbruchsreaktionen, so nimmt die Radikalkonzentration und damit die Geschwindigkeit der Gesamtreaktion lawinenartig zu, und es kommt zur Kettenexplosion (Explosion). Die Situation ist analog derjenigen bei Kernexplosionen, bei denen die Neutronen die Rolle der Kettenträger spielen.