Lexikon der Chemie: Kristall
Kristall, ein Festkörper, dessen Bausteine (Atome, Ionen oder Moleküle) in guter Näherung dreidimensional periodisch angeordnet sind. Ein K. entsteht aus einem Kristallkeim durch Wachstum (Kristallisation, Kristallzüchtung).
Als Idealkristall oder Idealstruktur des K. bezeichnet man eine mathematische Abstraktion eines in der Natur vorkommenden K., die streng periodisch ist. Abweichungen von der strengen Periodizität ergeben sich durch 1) die endliche Ausdehnung jedes realen K., 2) Kristallbaufehler, 3) die Schwingungen der Atome bzw. Ionen um ihre Gleichgewichtslagen, die selbst am absoluten Nullpunkt nicht völlig "einfrieren", und bewirken, daß Periodizität höchstens im Zeitmittel, nicht aber zu jedem beliebigen Zeitpunkt vorliegt. Die Untersuchung der Idealstruktur ist Gegenstand der Röntgenstrukturanalyse. Viele typische Eigenschaften von K. lassen sich aus der Idealstruktur erklären und ableiten. Dazu zählen die Symmetrieeigenschaften (s. u.), die bei unbehindertem Wachstum auftretenden ebenen Grenzflächen von K., die miteinander charakteristische Winkel einschließen, und die Anisotropie vieler Eigenschaften. Verschiedene Eigenschaften werden auch durch größere Abweichungen von der Idealstruktur nicht oder nur geringfügig beeinflußt, sie werden als störungsunempfindliche Eigenschaften (weniger zutreffend als strukturunempfindliche Eigenschaften) bezeichnet. Dazu zählen die Dichte, die Lichtbrechung und das Schmelzverhalten. Andere, störungsempfindliche Eigenschaften (strukturempfindliche Eigenschaften), z. B. die Festigkeitseigenschaften, die Ionen- und Elektronenleitfähigkeit in Ionen- bzw. Halbleiterkristallen und die optische Absorption, werden jedoch gerade durch die Abweichungen des wirklichen K. von dem idealen Aufbau weitgehend und oft sogar entscheidend beeinflußt. Dem Verständnis derartiger Eigenschaften von K. dient das Modell des Realkristalls oder die Realstruktur des K. Das Modell des Realkristalls beschreibt insbesondere Kristallbaufehler. Übergangsformen vom kristallinen zum flüssigen Aggregatzustand stellen die plastischen K. und die flüssigen K. dar.
Als Einkristall bezeichnet man einen aus einem einzigen, einheitlichen K. bestehenden Körper, in dem alle Teile in einer festen Orientierungsbeziehung zueinander stehen. In vielen Fällen, z. B. bei Metallen und keramischen Werkstoffen, tritt jedoch eine Vielzahl von Kriställchen (Kristallite) unterschiedlicher Orientierung innerhalb eines Festkörpers auf den man dann als polykristallin bezeichnet. Gesetzmäßige Verwachsungen von Einkristallen gleicher Art bezeichnet man als Zwillinge (bzw. Drillinge und allgemein Viellinge), die durch bestimmte "Zwillingsgesetze" beschrieben werden können.
Strukturbeschreibung. Die Untersuchung und Beschreibung der Struktur eines K. ist das Aufgabengebiet der Kristallstrukturlehre. Sie geht von der Betrachtung der Symmetrieeigenschaften (Symmetrie) als charakteristisches Kennzeichen des (Ideal-)K. aus. Das jeder Kristallstruktur zugrundeliegende Symmetrieelement ist die Translation. Man versteht darunter die (beliebig oft wiederholbare) Verschiebung eines Punktes um einen bestimmten Vektor a. Sie erzeugt eine (unendlich ausgedehnte) Punktreihe (eindimensionales Gitter). Der Betrag des Translationsvektors a, |a| = a0, wird Periode (Identitätsperiode, -abstand) genannt. Durch periodische Translation eines Punktes mit den Vektoren a, b und c entsteht ein dreidimensionales Punktgitter (Raumgitter, Abb. 1). Die Vektoren a, b und c nennt man die Basisvektoren des Gitters, sie bilden nach Übereinkunft ein Rechtssystem. Ihre Längen a0, b0 und c0 sowie die von ihnen eingeschlossenen Winkel α, β und γ werden als Gitterkonstanten bezeichnet. Das durch die drei Basisvektoren gebildete Parallelpiped heißt Elementarzelle. Da durch periodische Aneinanderreihung (unendlich) vieler Elementarzellen in den drei Translationsrichtungen das gesamte Gitter aufgebaut werden kann, genügt zu dessen vollständiger Beschreibung die Angabe der 6 Gitterkonstanten. Der Übergang von der mathematischen Abstraktion des Punktgitters zum K. wird dadurch vollzogen, daß an die Stelle jedes Gitterpunktes die gleiche Baugruppe von Atomen, Ionen oder Molekülen tritt. Sie wird die Basis der Kristallstruktur genannt, es gilt Gitter + Basis = Kristallstruktur. Aus dem Gitteraufbau folgen zwei der wichtigsten Eigenschaften eines K.: Er ist homogen, da er aus identischen Elementarzellen besteht, und zeigt das Merkmal der Anisotropie, da die Abstände der Gitterpunkte in verschiedenen Richtungen im allgemeinen verschieden sind.

Kristall. Abb. 1: Raumgitter mit Elementarzelle, Gitterkonstanten und Basisvektoren.
Kristall. Tab. 1: Die 7 Kristallsysteme.
| |||
| triklin | a0 ≠ b0 ≠ c0 ≠ a0 | α ≠ β ≠ γ ≠ α | keine |
| monoklin | a0 ≠ b0 ≠ c0 ≠ a0 | α = γ = 90°, β ≠ 90° | eine 2-zählige Drehachse oder eine Spiegelebene |
| orthorhombisch | a0 ≠ b0 ≠ c0 ≠ a0 | α = β = γ = 90° | jede beliebige Kombination dreier senkrecht aufeinanderstehender 2-zähliger Drehachsen oder Spiegelebenen |
| hexagonal | a0 = b0 ≠ c0 | α = β = 90°, γ = 120° | eine 6-zählige Drehachse oder eine 6-zählige Drehinversionsachse |
| rhomboedrisch | a0 = b0 = c0 | α = β = γ ≠ 90° | eine 3-zählige Drehachse oder eine 6-zählige Drehinversionsachse |
| tetragonal | a0 = b0 ≠ c | α = β = γ = 90° | eine 4-zählige Drehachse oder eine 4-zählige Drehinversionsachse |
| kubisch | a0 = b0 = c0 | α = β = γ = 90° | vier 3-zählige Drehachsen im Winkel von 109° 28″ zueinander |
Die Wahl der Elementarzelle ist zunächst nicht eindeutig, im Prinzip lassen sich beliebig viele unterschiedliche Elementarzellen und damit auch Tripel von Basisvektoren bzw. Sätze von Gitterkonstanten finden, mit deren Hilfe das Kristallgitter beschrieben werden kann. Bei der Präzisierung der Elementarzellenwahl berücksichtigt man nicht nur die Translationssymmetrie, sondern die Gesamtsymmetrie des K. und gelangt zu 7 Typen von Elementarzellen bzw. kristallographischen Achsensystemen, die die 7 Kristallsysteme genannt werden. Sie sind mit den sie charakterisierenden Festlegungen für die Gitterkonstanten in Tab. 1 zusammengestellt. Zuweilen werden auch das hexagonale und das rhomboedrische Kristallsystem als ein Kristallsystem betrachtet. Das trigonale Kristallsystem, das aus historischen und Zweckmäßigkeitsgründen ebenfalls häufig benutzt wird, kann gleichfalls dem hexagonalen Kristallsystem zugeordnet werden. Durch Vektoraddition der Basisvektoren erhält man Translationsgitter, in denen die Elementarzellen nur in ihren Ecken Gitterpunkte besitzen. Da ein solcher Gitterpunkt gleichzeitig 8 an der gleichen Ecke zusammenstoßenden Elementarzellen angehört und nur zu einem Achtel einer Elementarzelle zuzuordnen ist, besitzt diese insgesamt nur einen Gitterpunkt. Sie wird in diesem Fall als einfach primitiv bezeichnet. Den 7 Kristallsystemen entsprechen 7 Typen primitiver Elementarzellen (P-Gitter). Aus den bereits genannten Symmetriegründen muß man aber auch noch Translationsgitter berücksichtigen, deren Elementarzellen weitere zentrierende Gitterpunkte enthalten. Diese können das Zentrum (I-Gitter) oder die Flächenmitten der Elementarzelle (F-Gitter und A- oder B- oder C-Gitter) besetzen. Man spricht dann von zentrierten oder mehrfach primitiven Gittern. Zu den 7 primitiven Gittern kommen so noch 7 zentrierte Gitter hinzu, es ergeben sich insgesamt 14 verschiedene Typen möglicher Translationsgitter für K., die als Bravais-Gitter (nach A. Bravais, 1850) bezeichnet werden (Abb. 2, Tab. 2). Allen Kristallstrukturen liegen die 14 Bravais-Gitter zugrunde. Bei Stoffen, die nur aus einer Atomsorte bestehen, kann die Elementarzelle unmittelbar einem der in Abb. 2 dargestellten Typen entsprechen. So kristallisieren z. B. das Metall Kupfer in einem kubischen F-Gitter und das Metall Wolfram in einem kubischen I-Gitter. Die Strukturen komplizierter zusammengesetzter Verbindungen lassen sich durch Ineinanderstellen verschiedener Bravais-Gitter beschreiben (Natriumchloridtyp, Cäsiumchloridtyp).
Für die Strukturbeschreibung von K. benötigt man außer der Translation noch weitere kristallographische Symmetrieoperationen. Sie sind zusammen mit den entsprechenden Symmetrieelementen und deren international gebräuchlichen Symbolen nach Hermann-Mauguin in Tab. 3 aufgeführt. Die Beschränkung der kristallographischen Drehachsen auf solche der Zähligkeit 2, 3, 4 und 6 folgt zwangsläufig aus dem Gitterbau der K. Kristallstrukturen können kein, ein oder auch mehrere Symmetrieelemente enthalten. Dabei resultieren aus der Kombination bestimmter Symmetrieelemente häufig weitere. So ergibt z. B. die Kombination einer 2-zähligen Drehachse mit einer dazu senkrechten Spiegelebene automatisch ein Inversionszentrum, diese drei Symmetrieelemente sind also gesetzmäßig miteinander verknüpft. Die möglichen Kombinationen für die Elemente der Struktursymmetrie von K. werden als Raumgruppen bezeichnet. Die systematische Untersuchung zeigt, daß insgesamt 230 verschiedene Raumgruppen existieren (E. S. Fedorov 1885, A. Schoenflies 1889). Von diesen gehören 2 zum triklinen, 13 zum monoklinen, 59 zum orthorhombischen, 45 zum hexagonalen, 7 zum rhomboedrischen, 68 zum tetragonalen und 36 zum kubischen Kristallsystem. Jede Kristallstruktur kann ihrer Symmetrie nach einer der 230 Raumgruppen zugeordnet werden. Die Kenntnis der Raumgruppe ist Voraussetzung zur Aufklärung der Struktur eines K. mit Hilfe der Röntgenstrukturanalyse. Festkörperstrukturen mit nichtkristallographischer Symmetrie (z. B. mit fünfzähligen Drehachsen) kennt man seit einiger Zeit in Form der Quasikristalle.
Kristall. Tab. 2: Die 14 Bravais-Gitter .
| |||||
| triklin | 1 | primitv | P | 1 | |
| monoklin | 2 3 | primitiv basisflächenzentriert | P C | 1 2 | |
| orthorhombisch | 4 5 6 7 | primitv basisflächenzentriert innenzentriert, raumzentriert allseitig flächenzentriert | P C (bzw. A, B) I F | 1 2 2 4 | |
| hexagonal | 8 | primitiv | P | 1 | |
| rhomboedrisch | 9 | primitiv | R | 1 | |
| tetragonal | 10 11 | primitiv innenzentriert, raumzentriert | P I | 1 2 | |
| kubisch | 12 13 14 | primitiv innenzentriert, raumzentriert flächenzentriert | P I F | 1 2 4 |

Kristall. Abb. 2: Die 14 Bravais-Gitter (zur Numerierung vgl. Tab. 2).
Gestalt der K. Ein auffälliges, wenn auch nicht notwendiges Merkmal vieler K. sind ihre gut ausgebildeten Begrenzungsflächen. Mit der Untersuchung der Kristallgestalt, ihrer Gesetzmäßigkeiten und ihrer Entstehung beschäftigt sich die Kristallmorphologie. Zwischen der Gestalt und der Struktur der K. besteht eine enge Wechselbeziehung (Korrespondenzprinzip). Diese Korrespondenz gilt auch in bezug auf die Symmetrie: Die Symmetrie der äußeren Kristallgestalt (Makrosymmetrie) findet ihr Äquivalent in der strukturellen (Mikro-)Symmetrie. Es besteht aber ein entscheidender Unterschied zwischen beiden Symmetriearten: Die Translation ist wegen der Kleinheit der Translationsbeträge im Kristallgitter (Größenordnung: 100 pm) eine spezifisch strukturelle Symmetrieoperation. Sie wie auch die Symmetrieelemente mit Translationskomponente (Schraubenachsen und Gleitspiegelebenen) äußern sich nicht morphologisch. Bei systematischer Untersuchung der Kombinationsmöglichkeiten der restlichen Symmetrieelemente gelangt man zu den 32 kristallographischen Punktgruppen oder Kristallklassen (J. F. C. Hessel, 1830). Die Einordnung eines K. erfolgt stets in die höchstsymmetrische Kristallklasse, deren Symmetrieelemente er besitzt.
Eine Ebene im Kristallgitter, die durch mindestens drei nichtkollineare Gitterpunkte geht, wird als Netzebene bezeichnet. Wegen der Periodizität der Anordnung gehört zu jeder Netzebene eine Schar paralleler, äquidistanter Netzebenen, die Netzebenenschar. Der kürzeste Abstand zweier benachbarter Netzebenen heißt Netzebenenabstand oder Scharparameter. Die Korrespondenz zwischen Kristallmorphologie und -struktur äußert sich darin, daß die äußeren Kristallflächen parallel zu den Netzebenen des Kristallgitters liegen. Zur Kennzeichnung der räumlichen Lage einer Kristallfläche, also auch einer Netzebene, verfährt man wie folgt (Abb. 3): Man wählt einen Gitterpunkt als Ursprung und benutzt die Basisvektoren a, b und c als Achsen für ein Koordinatensystem. Von den Achsenabschnitten der betrachteten Netzebene (gemessen in Einheiten der Gitterkonstanten a0, b0 und c0) werden die Kehrwerte gebildet und die Brüche mit dem kleinsten gemeinsamen Vielfachen ihrer Nenner multipliziert. Die erhaltenen ganzen Zahlen hkl nennt man die Millerschen Indizes der Netzebene bzw. Fläche, das in Klammern eingeschlossene Indextripel (hkl) das Flächensymbol. Liegt die Netzebene zu einer Achse parallel, so ist der entsprechende Index gleich Null (z. B. (100)). Werden Achsen in ihrer negativen Richtung geschnitten, so wird das Minuszeichen über den betreffenden Index gesetzt (z. B. 2-12). Morphologisch wichtige, d. h. bei einer gegebenen Kristallart häufig vorkommende und gut ausgebildete Flächen weisen meist einfache Flächensymbole (kleine Millersche Indizes) auf. Sie entsprechen Netzebenen mit großen Scharparametern und einer dichten Besetzung mit Gitterpunkten.
Kristall. Tab. 3: Kristallographische Symmetrieoperationen.
| |||
| Punktsymmetrieoperationen 2-zählige Drehung | 2-zählige Drehachse | 2 | |
| Translation | |||
| 2-zählige Schraubung 3-zählige Schraubung 4-zählige Schraubung 6-zählige Schraubung | 2-zählige Schraubenachse 3-zählige Schraubenachse 4-zählige Schraubenachse 6-zählige Schraubenachse | 21 31, 32 41, 42, 43 61, 62, 63, 64, 65 | |
| Gleitspiegelung | Gleitspiegelebene mit Gleitkomponente | a/2 b/2 c/2 | a b c |
| (a + b)/2 oder (b + c)/2 oder (c + a)/2 oder (a + b + c)/2 (a + b)/4 oder (b + c)/4 oder (a + c)/4 oder (a + b + c)/4 | n d |
Die symmetrisch äquivalenten Flächen eines K. faßt man zu einem Komplex zusammen, der als Kristallform bezeichnet wird. So entsteht z. B. durch die Wirkung einer vierzähligen Drehachse eine Form von 4 Flächen (tetragonale Pyramide).
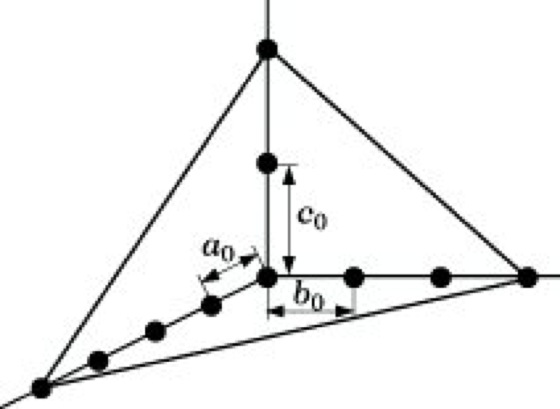
Kristall. Abb. 3: Lage einer Fläche (Netzebene) mit den Millerschen Indizes (346).
Die Anzahl der Kristallflächen bezeichnet man als Zähligkeit der Kristallform. Für die Kennzeichnung einer Kristallform verwendet man das Symbol {hkl}, wobei die Indizes hkl irgendeiner der zur Form gehörenden Flächen ausgewählt werden (z. B. Kennzeichnung der 6 Flächen des Würfels durch das Symbol {100}). Es gibt 48 verschiedene Kristallformen. Unter der Kristalltracht (Tracht) versteht man die Gesamtheit aller an einem K. vorhandenen Formen, unabhängig von ihrem Größenverhältnis. Der Kristallhabitus (Habitus) berücksichtigt dagegen die Größenverhältnisse der einzelnen Formen. Weist z. B. ein kubischer K. die Formen {100} (Würfel) und {111} (Oktaeder) auf, so spricht man bei stärkerer Ausbildung des Würfels von würfeligem Habitus, bei stärkerer Ausprägung des Oktaeders von oktaedrischem Habitus, wobei in beiden Fällen die Tracht die gleiche ist. Zur allgemeinen Charakterisierung des Habitus dienen Ausdrücke wie tafelig, prismatisch, isometrisch. Tracht und Habitus hängen vom inneren Aufbau des K., aber auch entscheidend von seinen Wachstumsbedingungen (Milieufaktoren) ab.
Die Charakterisierung durch eine bestimmte äußere Form geht zwar auf die Gitterstruktur der K. zurück, muß aber als unwesentlich betrachtet werden, da sie in vielen Fällen nur schwierig und häufig auch gar nicht möglich ist. Die röntgenographischen Untersuchungen haben gezeigt, daß fast alle festen Stoffe aus K. bestehen und die kristalline Form die Normalform des festen Zustandes ist.
Wenn Sie inhaltliche Anmerkungen zu diesem Artikel haben, können Sie die Redaktion per E-Mail informieren. Wir lesen Ihre Zuschrift, bitten jedoch um Verständnis, dass wir nicht jede beantworten können.