Ligandenfeldtheorie, behandelt die Veränderung der Elektronenstruktur des Zentralatoms einer Komplexverbindung unter dem Einfluß des von den Liganden erzeugten elektrischen Feldes. Dabei werden die Liganden durch Punktladungen bzw. Punktdipole dargestellt. Mitunter wird diese Betrachtungsweise in der Literatur auch als Kristallfeldtheorie bezeichnet, während man in den Begriff L. auch die elektronische Struktur der Liganden im Rahmen der Molekülorbitaltheorie (MO-Theorie) einbezieht. Die Erweiterung auf der Grundlage der MO-Methode wird MO-Theorie der Komplexe genannt.

Mit Hilfe der L. können insbesondere die optischen und magnetischen Eigenschaften von Komplexverbindungen der Übergangsmetalle erklärt werden. Die Anlagerung von Liganden führt zu einer energetischen Aufspaltung der entarteten D-Orbitale des Übergangsmetall-Ions, da an die Stelle der Kugelsymmetrie des freien Ions die jeweilige Symmetrie der Ligandenanordnung tritt. Aus der Richtungsabhängigkeit der D-Orbitale des Zentral-ions (quantenmechanisches Atommodell) und der daraus resultierenden unterschiedlichen elektrostatischen Abstoßung zwischen D-Elektronen und Liganden läßt sich die Aufspaltung der D-Niveaus für ein gegebenes Ligandenfeld in der Einelektronennäherung qualitativ erklären.

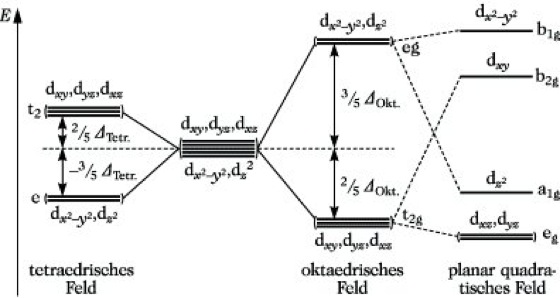
Ligandenfeldtheorie. Abb.: Aufspaltung eines D-Einelektronenzustandes in verschiedenen Ligandenfeldern.

Die Aufspaltung der D-Niveaus bei oktaedrischer, tetraedrischer und planar-quadratischer Ligandenanordnung zeigt die Abb. Die Energiedifferenz E(e_g) – E(t_2g) = Δ_Okt. bzw. E(t₂) – E(e) = Δ_Tetr. wird als (Liganden-) Feldstärkeparameter im oktaedrischen bzw. tetraedrischen Feld bezeichnet. Häufig verwendet man anstelle von Δ den Parameter Dq (Δ = 10 Dq). Die Besetzung der aufgespaltenen D-Orbitale mit Elektronen führt zu einem Energiegewinn, der als Ligandenfeldstabilisierungsenergie (Abk. LFSE) bezeichnet wird. Der Feldstärkeparameter Δ hängt vom Abstand Zentralion – Ligand und den Ladungen bzw. Dipolmomenten der Liganden ab. Er wird meist experimentell aus spektroskopischen Untersuchungen ermittelt und in der Wellenzahleneinheit cm^-1 angegeben. Ordnet man die Liganden nach steigenden Δ-Werten, d. h. nach zunehmender Stärke des Ligandenfeldes, so erhält man eine Reihe, die im wesentlichen für jedes Zentralion zutrifft (spektrochem. Reihe). Für wichtige Liganden erhält man die Sequenz: I^-< Br^-< Cl^-< SCN^-< F^-< OH^-< H₂O < NH₃< NO₂< CN^-. Betrachtet man Übergangsmetallionen mit mehreren D-Elektronen, so kann man zunächst unter Vernachlässigung der Elektronenwechselwirkung durch Besetzung der Einelektronenzustände des Zentralions Konfigurationen erzeugen. In Abhängigkeit von der Größe des Feldstärkeparameters Δ ist dies auf verschiedene Weise möglich. So bewirkt ein starkes Ligandenfeld bei einem oktaedrischen Fe³⁺-Komplex eine große Aufspaltung der D-Niveaus, und die fünf D-Elektronen des Fe³⁺-Ions besetzen daher unter teilweiser Spinpaarung die energetisch günstigen t_2g-Niveaus. Der Gesamtspin des Komplexes beträgt S = 1/2(low-spin-Komplex). Ein solcher Fall liegt z. B. im [Fe(CN)₆]^3- vor. Bei einem schwachen oktaedrischen Ligandenfeld, z. B. im [FeF₆]^3--Komplex, ist der Energieunterschied zwischen den e_g- und t_2g-Niveaus kleiner als im [Fe(CN)₆]^3-. Der für die Besetzung der höheren e_g-Niveaus erforderliche Energieaufwand ist kleiner als der Energiegewinn, der aus der verminderten Elektronenwechselwirkung zwischen Elektronen mit gleichem Spin resultiert (Hundsche Regel). Daher werden im [FeF₆]^3--Komplex die t_2g- und die e_g-Orbitale zunächst einzeln und mit parallelem Spin besetzt. Der Gesamtspin des [FeF₆]^3--Komplexes beträgt S = ⁵/₂ (high-spin-Komplex). Anhand dieser Näherungsbetrachtung können die magnetischen Eigenschaften der Komplexe gedeutet werden. Die Berücksichtigung der Elektronenwechselwirkung und damit die Ermittlung des Termsystems eines Übergangsmetall-Komplex-Ions kann auf zwei Wegen erfolgen: 1) Ist die Wechselwirkung zwischen den einzelnen D-Elektronen groß gegenüber der Wirkung des Ligandenfeldes (Methode des schwachen Feldes), so erhält man aus der Konfiguration d^N des Zentralions die Terme ^2s+1L des freien Ions (Multiplettstruktur). Die Wirkung des Ligandenfeldes auf die Terme des freien Ions führt zum Termsystem des Komplex-Ions. 2) Ist die Wirkung des Ligandenfeldes stark gegenüber der Elektronenwechselwirkung, so wird zunächst der Einfluß des Ligandenfeldes auf die d^N-Konfiguration des Zentralions betrachtet. Die Besetzung der Einelektronenzustände unter Berücksichtigung des Pauli-Prinzips ergibt die Konfigurationen des Komplex-Ions, z. B. tⁿ_2ge_g^N-n im oktaedrischen Feld, wobei n und N Elektronenbesetzungszahlen der Energieniveaus darstellen. Die anschließende Erfassung der Elektronenwechselwirkung führt zum Termsystem des Komplex-Ions (Methode des starken Feldes). Für genauere Untersuchungen ist bei der Methode des starken Feldes die Konfigurationenwechselwirkung und bei der des schwachen Feldes die Termwechselwirkung zu berücksichtigen. Beide Wege führen zum gleichen Ergebnis. Die Resultate quantitativer Untersuchungen über Termsysteme von Komplex-Ionen werden in Form von Termdiagrammen dargestellt, indem die Termenergie als Funktion des Ligandenfeldparameters angegeben wird. Solche Termdiagramme sind von Orgel nach der Methode des schwachen Feldes für einige Übergangsmetall-Komplex-Ionen angegeben worden. Analoge Untersuchungen erfolgten von Tanabe und Sugano nach der Methode des starken Feldes. In den Tanabe-Sugano-Diagrammen wird die Termenergie in der Form E/B als Funkton von Δ/B dargestellt. Die Größe B ist ein Maß für die Elektronenwechselwirkung und wird als Racah-Parameter bezeichnet.